Раздел «Линейное программирование»
СОДЕРЖАНИЕ
Введение |
|
|
§1. |
Линейное программирование. Сущность линейного программирования |
5-13 |
§2. |
Геометрический метод решения задач линейного программирования |
13-16 |
§3. |
Симплексный метод решения задач |
16-27 |
§4. |
Транспортная задача |
27-39 |
Введение
Среди задач математического программирования лучше всего изученными являются так называемые задачи линейного программирования. Это задачи, в которых целевая функция является линейной функцией независимых переменных, и условия, определяющие допустимые значения этих переменных, имеют вид линейных уравнений или линейных неравенств.
Задачи линейного программирования являются математическими моделями многочисленных задач технико-экономического содержания. Такие задачи довольно часто встречаются на практике, например, при решении проблем, связанных с поиском способов оптимального распределения и использования ограниченных ресурсов, управления и планирования производственных процессов и т.д.
Целью настоящей работы является знакомство с методами оптимизации, приобретение навыков по решению задач линейного программирования.
Учебно - методическое пособие адресовано студентам всех специальностей СПО по разделу «Линейное программирование».
§1. Линейное программирование. Сущность линейного программирования
Линейное программирование есть совокупность математических методов нахождения минимальных и максимальных значений линейных функций в области неотрицательных значений переменных величин при ограничениях, заданных системой линейных уравнений или неравенств.
Определение. Линейная функция вида:
(1)
максимум или минимум, которой находится в задаче линейного программирования, называется целевой функцией.
Задачей линейного программирования называется задача вида:
Найти
целевой функции (1)
при условии, что на переменные
наложены ограничения в виде линейных
равенств или неравенств:
(2)
Искомые переменные
могут выражать: объемы производства
различных видов продукции, планируемые
под сельскохозяйственные культуры,
посевные площади, количество составляющих
веществ в различных смесях, количество
единиц приобретаемого продукта и т.д.
Функция
может представлять собой стоимость
выпускаемой продукции, ожидаемый урожай,
доход, ущерб, а условия ограничений,
которым подчинены
,
отражают ограниченность имеющихся
естественных материальных, денежных
ресурсов, требования к количеству
продукции или производственных мощностей.
Определение. Совокупность значений переменных удовлетворяющих условиям задачи линейного программирования и образующих область определения функции , называется областью допустимых значений переменных.
Определение Набор значений из допустимой области, при которой целевая функция (1) принимает наибольшее или наименьшее значения называется решением задачи линейного программирования или оптимальным планом.
Замечание:
определение минимального значения
целевой функции
можно свести к определению максимального
значения функции
,
так как
.
Определение. Критерием оптимальности называется некоторый показатель, имеющий экономическое содержание, служащий формализацией конкретной цели управления и выражаемый при помощи целевой функции. Задача линейного программирования может быть записана в матричной форме:
при ограничениях
(3)
в координатной форме:
, при ограничениях
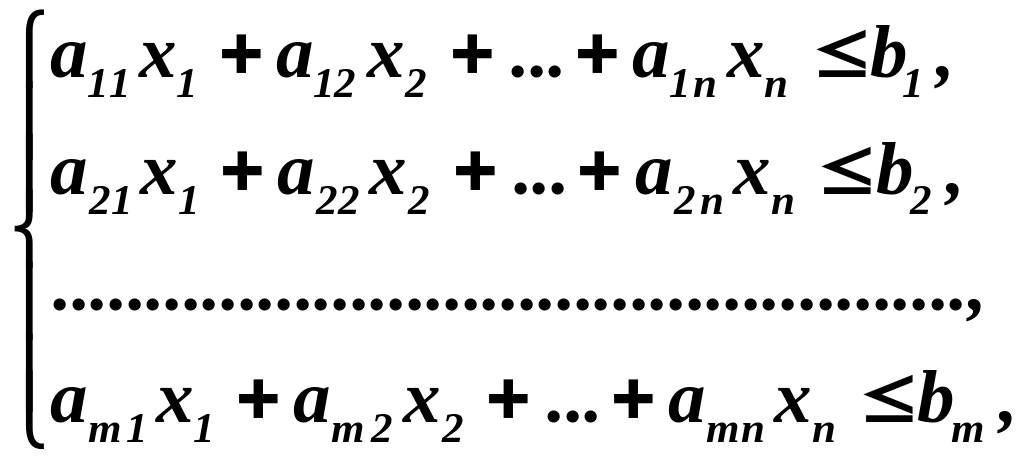
с использованием знака суммирования:
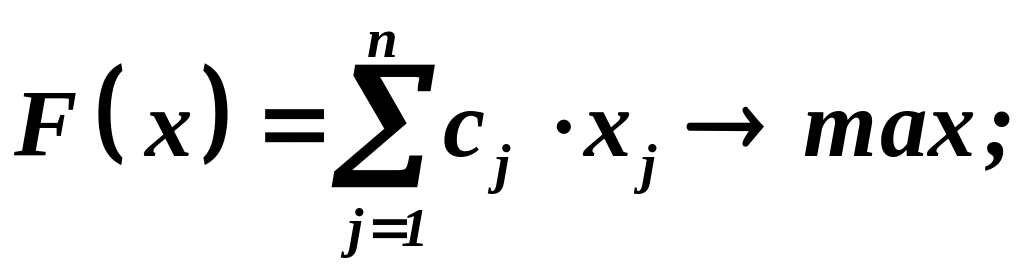при ограничениях
Каноническая модель задачи линейного программирования имеет вид:
.
(4)
Математическая модель экономического объекта – это его отображение в виде математических соотношений (функций, уравнений, неравенств, графиков и т.д.).