32. Похідна в заданному напрямку

В математичному аналізі, похідна за напрямком - це узагальнення поняття похідної на випадок функції кількох змінних. Похідна за напрямом показує, наскільки швидко функція змінюється при русі вздовж заданого напряму.

Похідна функції однієї змінної показує, як змінюється її значення при малій зміні аргументу. Якщо ми спробуємо за аналогією визначити похідну функції багатьох змінних, то зіткнемося з труднощами: у цьому випадку зміна аргументу (тобто точки в просторі) може відбуватися в різних напрямках, і при цьому будуть виходити різні значення похідної. Саме це міркування і призводить до визначення похідної за напрямом.

Розглянемо функцію   від   аргументів на околиці точки   . Для будь-якого одиничного вектора   визначимо похідну функції   в точці   за напрямом   наступним чином:

Значення цього виразу показує, як швидко змінюється значення функції при зсуві аргументу в напрямку вектора   .

Якщо напрямок сонаправленностью з координатною віссю, то похідна за напрямом збігається з похідної по цій координаті.

33. Градієнт

Градієнт, як завжди вважають, — векторна величина, яка визначає в кожній точці простору не лише швидкість зміни, а й напрямок найшвидшої зміни функції, що залежить від координат. Але при замінах координат, градієнт перетворюється інакше, ніж вектор, і тому його не можна розглядати як справжній вектор.

Для скалярного поля   градієнт визначається формулою

де  ,  ,   - орти системи відліку.

Це означення узагальнюється на простори будь-якої розмірності

.

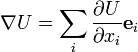34. Зв'язок між похідною за напрямко та градієнтом функції

Похідну за напрямом діфференцііруемой за сукупністю змінних функції можна розглядати як проекцію градієнта функції на цей напрямок, або інакше, як скалярний твір градієнта на орт напрямки:

 ,

де   - Орт напряму. Звідси випливає, що максимальне значення в точці похідна за напрямом приймає, якщо напрямок збігається з напрямком градієнта функцій в даній точці. Також видно, що значення похідної по напрямку не залежить від довжини вектора   .

35. Частинні похідні вищих порядків. Рівність змішаних похідних.

Частинною похідною другого порядку функції z= f(x,y) називається частинна похідна від частинної похідної першого порядку. ; ; ;

- повторні; - змішані.

3 6. Екстремум. Означення, необхідні умови.

М0(х0,у0)

У1 + - + … + -

y=f(x); y`=0; y`-

Х2 х1 х2 х3 хн

Х1

Внутрішня частина круга з центром М0 х радіусом r називається окіл і позначається О r(М0).

Точка М0 з координатами (х0,у0) називається точкою максимуму функції z= f(x,y) якщо для любих точок н з цього кола виконується рівність: . Точка М1 називається точкою мінімуму функції z= f(x,y) якщо існує такий окіл . Необхідна умова екстремуму: якщо М0(х0,у0) є точкою екстремуму функції z= f(x,y) то z`x в цій точці =0, z`y=0. Або похідні в цих точках не існують. або . Дана умова є тільки необхідною для існування екстремуму, але не достатньою. Якщо точка М0 задовольняє цю умову то це не гарантія що вона є екстремальною. Такі точки називаються підозрілими на екстремум або критичними точками.

; ; ;