1. Загальне рiвняння площини. Розміщення площини в системi координат в залежності від значень коефіцієнтів в рiвнянні.

Якщо в р-ні (1) розкрити дужки і перегрупувати доданки, то одержимо: Ах+Ву+ Cz-Ах0-Ву0- Cz0=0.

Ах+Ву+ Cz+D=0 (2) Загальне р-ня площини. А,В,С,D – відомі числа. х,у,z – змінні.

Розміщення площини в системі коорд., якщо деякі з коеф. А,В,С,D рівні 0:

1)А=0; В,С,D0; Ву+ Cz+D=0; площина  || Ox. 2)В=0;  || Oу. 3)С=0;  || Oz; 4)D=0; Ах+Ву+ Cz=0; О(0,0,0) є ;

5)В=А=0; Cz+D=0; z=с;  || хОу; 6)А=С=0; у=В;  || хОz; 7)В=С=0; х=а;  || уОz; 8)А=D=0; Ву+ Cz=0; Ох є ;

9)В=D=0; Ах + Cz=0; Оу є ; 10)С=D=0; Ах+Ву=0; Оz є ; 11)А=В=D=0; С0; Сz=0; z=0; = хОу;

12)В=С=D=0; А0; Ах=0; х=0; = уОz; 13)А=С=D=0; В0; Ву=0; у=0; =|| хОz; 14) А=В=С=0; D0; D=0;  не існує.

15)А=В=С=D=0; 0=0; =R^3.

2. Рівняння площини у відрізках та його застосування.

Z

с С (0,0,с)

О В (0,в,0) у

в

А(а,0,0) а

Х

3. Рівняння площини яка проходить через три точки.

М: М1М; М1М2; М1М3 – компленарні вектори.

М1М*М1М2*М1М3=0 - змішаний добуток.

М1М={x-x1; y-y1; z-z1}

M1M2={x2-x1; y2-y1; z2-z1}

M1M3={x3-x1; y3-y1; z3-z1}

(х1,у1, z1) М(х,у, z)

М1

М2(х2,у2, z2)

М3(х3,у3, z3)



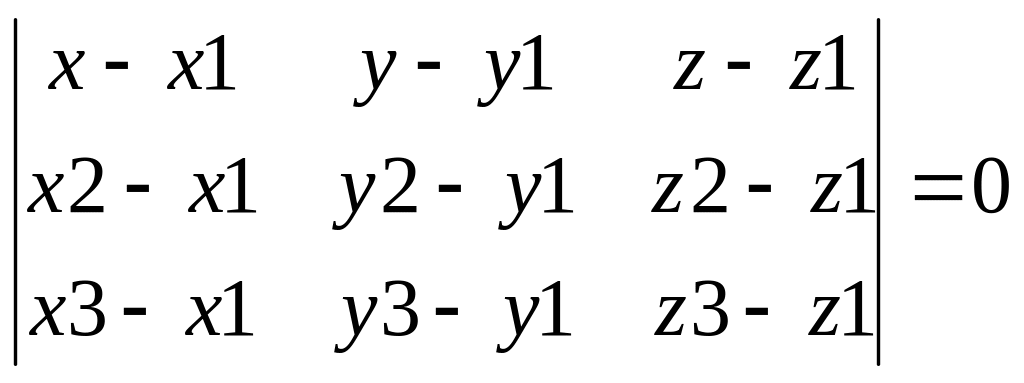(4) Р-ня площини що проходить через три точки. Див.пр.

4. Рівняння площини, що проходить через дві точки паралельно вектору.

М1(х1,у1, z1) М(х,у, z)

(5) Див.пр.

 М2(х2,у2, z2)

={m,n,p}

5. Рівняння площини, що проходить через одну точку паралельно двом даними векторам.

={m2,n2,p2} 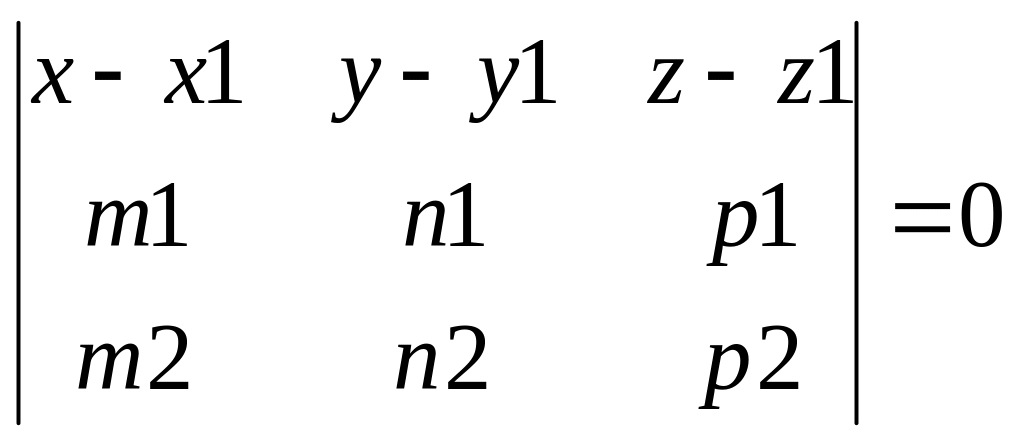(6) Див.пр.

={m1,n1,p1}

M1(x1,y1,z1)

M2(x2,y2,z2)



6.Кут між двома площинами. Умови паралельності та перпендикулярності двох площин.

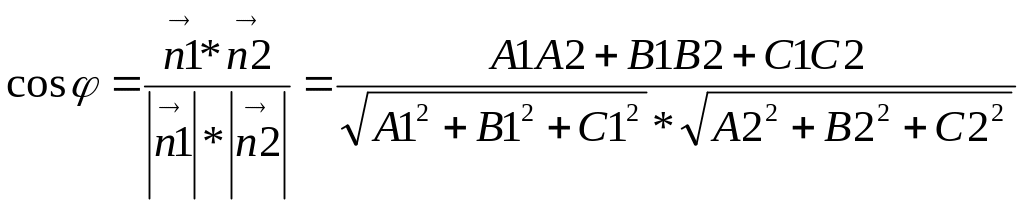 1: A1x+B1y+C1z+D1=0

2: A2x+B2y+C2z+D2=0 (7)

-?

1={A1,B1,C1}

2={A2,B2,C2}

А)Умова паралельності площин: 1//2 => 1// 2; A1/A2=B1/B2=C1/C2 (8)

Б)Умова перпендикулярності: 12 => 1 2; A1A2+B1B2+C1C2=0 (9) Див.пр.+рис.

7.Канонічні рівняння прямої в просторі.

Якщо відомі координати точки М (х,у, z) , що лежить на прямій і напрямного вектора ={m,n,p}, то р-ня прямої можна записати у канонічному вигляді: . З цього ми бачимо, що пряма лінія у просторі описується системою двох р-нянь першого степеню відносно змінних х,у, z. Див. пр..

8.Загальне рівняння прямої у просторі.

Пряму лінію у просторі можна розглядати як лінію перетину двох площин.

L1:A1x+B1y+C1z+D1=0

L2: A2x+B2y+C2z+D2=0

Загальне р-ня прямої у просторі.

Див.пр.

L1

l

L2

9. звязок між канонічним та зальними рівняннями прямої

Пряма задана загальними рівняннями  

Записати її канонічні рівняння.

Розв'язання.

Для запису канонічних рівнянь прямої у вигляді слід знати дві точки цієї прямої   та . В якості координат цих точок можна взяти два довільних розв'язки даної системи рівнянь, наприклад,  і  . Тоді шукані рівняння матимуть вигляд 

 або 

1

ММ1 || М1М2

М1М = {x-x1;y-y1;z-z1}

М1М2 = {x2-x1;y2-y1;z2-z1}

Р-ня прямої що проходить через дві точки

М2(х2,у2, z2)

0.Рівняння прямої що проходить через дві задані точки.

l

М(х,у, z)

М1(х1,у1, z1)