3.3. Влияние пороков на работу элементов деревянных конструкций

Нормативные сопротивления древесины вычисляются по результатам испытания чистой древесины. На практике в элементах конструкций неизбежно присутствуют пороки древесины, оказывающие влияние на прочность элементов.

Сучки – образуют отверстия, уменьшают эффективную площадь поперечного сечения, создают концентрации напряжений. Существенно уменьшают прочность при растяжении.

Наклон волокон (косослой) – увеличивает напряжения, направленные поперек волокон, а в этом направлении прочность древесины в 20 – 25 раз меньше, чем вдоль волокон. Косослой в большей мере влияет на прочность при растяжении, чем при сжатии.

Трещины – опасны при работе древесины на скалывание.

Влияние пороков снижает прочность элементов по сравнению с чистой древесиной при растяжении примерно в 2,8 раза, при сжатии – в 1,5 раза.

В гнутых деревянных элементах, например в арках, рамах, верхних поясах сегментных ферм, возникают напряжения от гнутья, которые снижают несущую способность элемента. Снижение это учитывается коэффициентом (п. 6.30, [11] ).

При проектировании клееных конструкций надо указывать вид применяемого клея в зависимости от условий эксплуатации. В основном при склеивании древесины применяются фенольный, резорциновый, фенольно-резорциновый, карбамидно-меламиновый, карбамидный клеи. При склеивании древесины с металлом применяются эпоксидный, фенольный клеи [табл.2, 11].

3.4. Расчет элементов деревянных и пластмассовых конструкций цельного сечения

Элементы деревянных и пластмассовых конструкций рассчитывают на растяжение, сжатие, изгиб, растяжение или сжатие с изгибом (сложное напряженное состояние), смятие и скалывание от действия усилий N, Q, M.

На растяжение работают нижние пояса ферм, затяжки арок и стержни других сквозных конструкций (рис. 3.1).

Проверка прочности центрально-растянутых элементов производится по формуле

(3.35)

где N – расчетное продольное усилие, кН; 10 – коэффициент, учитывающий соотношение единиц (1 кН/см²=10 МПа). Площадь F_нт=F_бр–F_осл – расчетная площадь нетто наиболее ослабленного сечения (от отверстий, врезок, врубок). Ослабления считаются совмещенными в одном сечении при расположении их на участке длиной не более 20 см (рис. 3.2). При несимметричном ослаблении относительно центра тяжести поперечного сечения элемента, его рассчитывают как внецентренно растянутый.

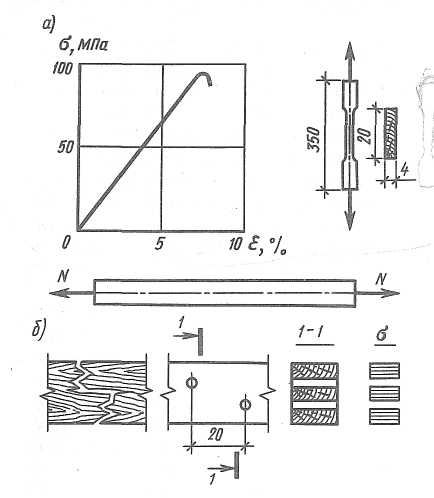
Рис. 3.1. Растянутый элемент:

а )–график деформаций и образец; б) – схемы рабо­ты, разрушение и

эпюра напряжений

Рис. 3.2. Центральное растяжение элемента

Коэффициент условий работы m_p=0,8 учитывает снижение расчетного сопротивления материала, вызванное концентрацией напряжений в ослабленных сечениях. Прочность растянутых деревянных элементов снижается.

Растянутые элементы должны проектироваться из древесины не ниже второго сорта по качеству. Ввиду низкой прочности древесины на растяжение поперек волокон, конструкции или соединения проектируют на работу материала вдоль волокон.

На сжатие работают стойки, подкосы, верхние пояса и отдельные стержни ферм (рис. 3.3).

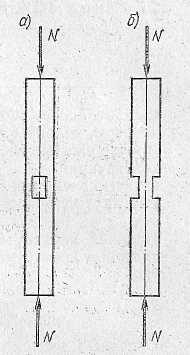
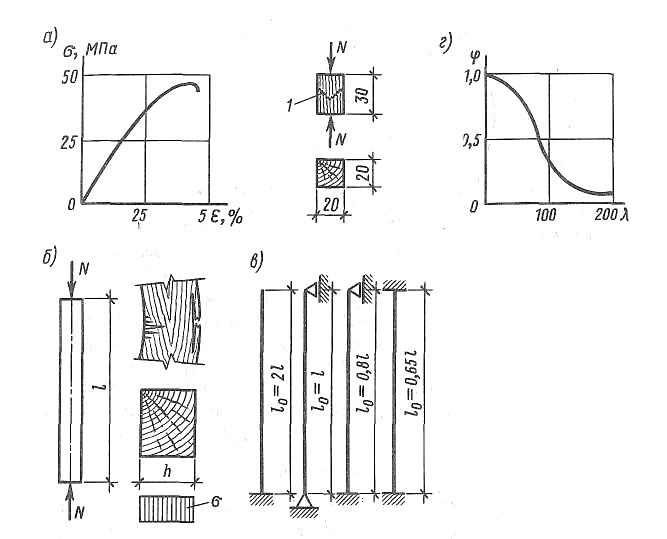
Рис. 3.3. Сжатый элемент:

а) – график деформаций и образец; б) – схемы работы, разрушения и эпюра

напряжений; в) – типы закрепления концов и расчетные длины; г) – гра-

фик коэффициентов устойчивости φ в зависимости от гибкости λ

Разрушение центрально-сжатых элементов может произойти от потери устойчивости или прочности. Центрально сжатые элементы рассчитывают по формулам:

– на прочность (3.36)

– на устойчивость (3.37)

где N – расчетное сжимающее усилие; F=(F_бр– F_осл), как для растянутых элементов; F_расч – расчетная площадь поперечного сечения при проверке устойчивости. Принимается равной F_бр – при отсутствии ослаблений; при ослаблениях, не выходящих на кромку, если площадь ослаблений F_осл≤0,25F_бр, то F_расч= F_бр; при F_осл>0,25 F_бр, при симметричных ослаблениях, выходящих на кромки ,F_расч= F_нт (рис. 3.3). При несимметричных ослаблениях, выходящих на кромку, элементы рассчитываются как внецентренно сжатые.

Коэффициент продольного изгиба φ отношение критического напряжения, при котором стержень теряет устойчивость, к пределу прочности материала на сжатие:

(3.38)

Коэффициент φ обычно меньше 1, зависит от гибкости стержня λ. При λ>λ_min коэффициент φ находится по формуле Эйлера:

(3.39)

где значение заменяется на коэффициент А и при λ>λ_min находится по формулам [11].

При λ<λ_min в формулах значение коэффициента А уменьшается. Например, для фанерных труб и профилей (швы, уголки) можно применять формулы:

– для фанерных труб при λ>69 φ=2390/λ², при λ≤69 φ=1-1,046(λ/100)²;

– для фанерных профилей при λ>60 φ=2150/λ², при λ≤60 φ=1-1,12(λ/100)²,

При λ>λ_min :

– для всех стеклопластиков

(3.40)

– для фанерных элементов

; (3.41)

– для деревянных элементов

(3.42)

Гибкость элементов λ определяют в зависимости от их расчетной длины и радиуса инерции поперечного сечения по формуле

, (3.43)

где . Гибкость не должна превышать значений, приведенных в табл. 14 [11] .

Расчетная длина зависит от способа закрепления элемента и вычисляется по формуле (п. 4.21 и 6.25 [11]).

На изгиб работают настилы, обрешетки, обшивки плит и панелей, стропильные ноги, прогоны, балки (рис. 3.4).

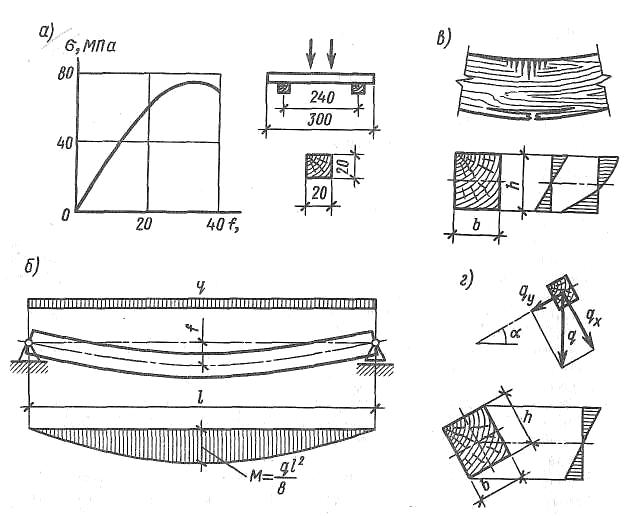
Рис. 3.4. Изгибаемый элемент:

а) – график прогибов и образец; б) – схема работы и эпюры изгибающих мо­ментов; в) – схема разрушения и эпюры нормальных напряжений;

г) – схема работы при косом изгибе и эпюра напряжений

Изгибаемые элементы рассчитываются на прочность и жесткость (по деформациям или прогибам), т.е. по двум предельным состояниям.

Различают два вида работы элементов на изгиб: простой изгиб, когда нагрузка действует в плоскости одной из главных осей инерции поперечного сечения элемента и косой изгиб, когда направление нагрузки не совпадает ни с одной из главных осей инерции сечения (рис. 3.4, б).

Изгибаемые элементы на прочность при простом изгибе рассчитываются по формуле

(3.44)

где W_расч – расчетный момент сопротивления по площади нетто. Для клееных (гнутых) деревянных элементов

W_расч=W_нтm_б(m_гн), (3.45)

для составных стержней на податливых связях

W_расч=W_нтk_w. (3.46)

Коэффициенты m_гн, m_б, k_w даны в [11] .

При простом изгибе сечение по заданному изгибающему моменту М подбирается по формуле

(3.47)

По найденному моменту сопротивления находят размеры поперечного сечения и подбирают пиломатериал по сортаменту, например для прямоугольного сечения,

. (3.48)

При косом изгибе (рис. 3.4, г) расчет элементов на прочность по нормальным напряжениям производится по формуле

(3.49)

где М_х и М_y – составляющие расчетного изгибающего момента относительно главных осей x и y; W_x и W_y – расчетные моменты сопротивления поперечного сечения нетто для осей х и y; R_u – расчетное сопротивление изгибу.

Для подбора прямоугольного сечения косоизгибаемого элемента можно пользоваться формулами:

, (3.50)

При подборе сечения изгибаемых элементов по нормальным напряжениям в некоторых случаях необходима проверка скалывающих напряжений в местах наибольших сдвигающих усилий, например в балках двутаврового сечения с тонкой стенкой, в прямоугольных балках при наличии значительных поперечных сил, расположенных близко к опорам, особенно для коротких балок ( . Проверка на скалывание производится по формуле Журавского

(3.51)

Для изгибаемых элементов из конструкционных пластмасс проверка на скалывание обязательна.

Расчет изгибаемых элементов на жесткость (по деформациям) заключается в определении прогиба от нормативных нагрузок и сопоставлении его со значением допустимого прогиба, установленного по СНиП II-25-80*.

Прогибы вычисляются как относительная величина в предположении упругой работы древесины по формулам сопротивления материалов в соответствии с расчетными схемами. Необходимо выполнение условия

. (3.52)

Влияние касательных напряжений на прогиб балок прямоугольного сечения не учитывают, при расчете клеедощатых балок таврового сечения с тонкими стенками прогиб считают и от действия касательных напряжений.

Для изгибаемых элементов из пластмасс необходимо учитывать влияние как нормальных, так и касательных напряжений. Вызываемые касательными напряжениями сдвиги могут оказать существенное влияние на прогиб.

Прогиб элементов с учетом воздействия касательных напряжений определяют по формуле

(3.53)

где – прогиб без учета касательных напряжений; – коэффициент, зависящий от схемы нагружения внешней нагрузкой; – коэффициент, зависящий от формы поперечного сечения и коэффициента Пуассона ( ), материала балки.

Изгибаемые элементы настилов, кроме обычного их расчета на прогиб от полной нормативной нагрузки, проверяют на гибкость путем расчета на прогиб от сосредоточенного груза 60 кг (0,6 кН); прогиб при этом не должен превышать 0,05 см.

Полный пролет балки при косом изгибе равен геометрической сумме прогибов и от составляющих сил и :

. (3.54)

Косой изгиб существенно увеличивает размеры прямоугольного сечения (прогонов), поэтому следует конструктивными мероприятиями добиваться того, чтобы основная нагрузка действовала в плоскости наибольшей жесткости. Например, прогоны наклонной кровли должны опираться на подкладки, обеспечивающие вертикальное расположение сечения, или скатная составляющая q_y может быть воспринята элементами кровли, если она состоит из настилов двух направлений. Для той же цели могут быть использованы вспомогательные стропильные ноги, скрепленные друг с другом в коньке и с прикрепленными к ним прогонами кровли.

Наименьшая площадь поперечного сечения прямоугольного прогона при косом изгибе из условия прочности получается при соблюдении отношения

(3.55)

а из условия прогиба при отношении

. (3.56)

В балках круглого сечения явления косого изгиба нет.