Задания:

В данных задачах составить экономико-математическую модель.

1. Для производства двух видов изделий А и В предприятие использует три вида сырья. Другие условия задачи приведены в таблице.

Таблица 5

Вид сырья	Общее количество сырья, кг	Нормы расхода сырья на одно изделие, кг
		А	В
S1	300	12	4
S2	120	4	4
S3	252	3	12
Прибыль от реализации изделия, ден. ед.		30	40

Составить такой план выпуска продукции, при котором прибыль предприятия от реализации продукции будет максимальной при условии, что изделий В надо выпускать не менее, чем изделий А.

2. Рацион питания для животных на ферме состоит из двух видов кормов I и II. Один килограмм корма I стоит 80 руб. и содержит: 1 ед. жиров, 3 ед. белков, 1 ед. углеводов и 2 ед. нитратов. Один килограмм корма II стоит 10 руб. и содержит: 3 ед. жиров, 1 ед. белков, 8 ед. углеводов и 4 ед. нитратов.

Составить наиболее дешевый рацион питания, обеспечивающий жиров не менее 6 ед., белков не менее 9 ед., углеводов не менее 8 ед., а нитратов не более 16 ед.

Литература.

1. Исследование операций в экономике / п/р Н.Ш Кремера. – М.: ЮНИТИ, 2000. – 407с.

2. Акулич И.Л. Математическое программирование в примерах и задачах. – М.: Высшая школа, 1986.

3. Банди Б. Основы линейного программирования. – М.: Радио и связь, 1989.

4. Вентцель Е.С. Исследование операций. – М.: Сов. радио, 1972.

5. Малик Г.С. Основы экономики и математические методы в планировании. – М. "Высшая школа", 1988

Интернет – ресурсы:

1. Справочные материалы по высшей математике http://primat.at.ua

2. Электронные учебные пособия http://book.ru-deluxe.ru

Лекция 5. Геометрический смысл решений неравенств и их систем неравенств. План.

1. Геометрический смысл решения неравенства с двумя переменными.

2. Решение системы линейных неравенств.

3. Возможные варианты решений неравенств.

Рассмотрим линейные неравенства с двумя переменными .

Теорема: Множеством решений линейного неравенства с двумя переменными является одна из двух полуплоскостей, на которые вся плоскость делиться граничной прямой , включая и эту прямую (если неравенство н строгое, то сама прямая не входит в решение). А другая полуплоскость с этой же граничной прямой будет являться решением неравенства .

Что бы определить, какая из полуплоскостей является решением неравенства, воспользуемся правилом: если полуплоскость является решением линейного неравенства, то все точки данной полуплоскости удовлетворяют неравенству, то есть превращают его в истинное выражение при подстановке в неравенство координат точки. Если полуплоскость не является решением неравенства, то ни одна его точка не удовлетворяет неравенству, а значит, при подстановки ее координат в неравенство выражение становится ложным. Следовательно, для выбора полуплоскости, являющуюся решением неравенства, достаточно проверить истинность или ложность неравенства в любой точке любой полуплоскости. Чаще всего, если прямая не проходит через начало координат, проверяют истинность неравенства в точке (0;0).

Теорема: Множеством решений совместной системы m линейных неравенств с двумя переменными:

является выпуклым многоугольным множеством, которое образуется пересечением полуплоскостей, каждая из которых – это решение одного из неравенств системы.

Для решения системы линейных неравенств графически, необходимо на одном графике изобразить решение каждого неравенства системы, а затем выбрать их общую часть.

Пример 5

Решить систему неравенств:

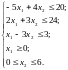
Построим граничную прямую для первого неравенства: 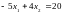(I). Она проходит через точки:

х1	0	-4
х2	5	0

Выберем полуплоскость, которая является решением данного неравенства. Это будет полуплоскость, содержащая начало координат -5·0+4·0≤20.

Построим граничную прямую для второго неравенства: (II). Она проходит через точки:

х1	0	12
х2	8	0

Выберем полуплоскость, которая является решением данного неравенства. Это будет полуплоскость, содержащая начало координат 2·0+3·0≤24

Построим граничную прямую для третьего неравенства: (III). Она проходит через точки:

х1	0	-4
х2	5	0

Выберем полуплоскость, которая является решением данного неравенства. Это будет полуплоскость, содержащая начало координат 0-3·0≤3

Граничной прямой четвертого неравенства будет ось Ох₂, а решением неравенства полуплоскость справа от оси.

Граничными прямыми пятого и шестого неравенств (двойного неравенства) будут соответственно ось Ох₁ и прямая х₂=6. А решение будет полоса между двумя прямыми: x₂=0 и х₂=6.

Построим все решения на одном графике.

Найдем область, в которой все неравенства будут истинны одновременно. Эта область содержит точку с координатами (0;0).

На графике это область OABCDE (см. рисунок 1)

Рисунок 1

При решении системы неравенств не всегда получается замкнутая многоугольная область. Область может получиться неограниченной областью, или быть одной точкой, лучом, отрезком. Если система неравенств несовместна, то не все полуплоскости пересекаются. Возможные варианты показаны на рисунке 2.

Рисунок 2