Литература.

1. Исследование операций в экономике / п/р Н.Ш Кремера. – М.: ЮНИТИ, 2000. – 407с.

2. Вентцель Е.С. Исследование операций. Задачи, принципы, методология – М.: Наука, 1980.

Замков О.О., Толстопятенко А.В., Черемных Ю.Н. Математические методы в экономике. – М.: Издательство «Дело и сервис», 2001.

Интернет – ресурсы:

1. Справочные материалы по высшей математике http://primat.at.ua

2. Электронные учебные пособия http://book.ru-deluxe.ru

Лекция 4. Основные понятия линейного программирования. План.

1. Область применения.

2. Примеры задач линейного программирования.

   1. Задача об использовании ресурсов.

   2. Задача о диете.

3. Общая задача линейного программирования.

4. Виды задач линейного программирования.

5. Приведение задач линейного программирования к каноническому виду.

Задачами линейного программирования называются задачи, в которых линейны как целевая функция, так и ограничения в виде равенств и (или) неравенств. Линейное программирование представляет собой наиболее часто используемый метод оптимизации. К числу задач линейного программирования относятся:

1. рациональное использование сырья и материалов; задачи оптимизации раскроя;

2. оптимизации производственной программы предприятий;

3. оптимального размещения и концентрации производства;

4. на составление оптимального плана перевозок, работы транспорта;

5. управления производственными запасами;

6. и многие другие, принадлежащие сфере оптимального планирования.

По оценкам американских экспертов на линейное программирование приходится около 75% от общего числа применяемых оптимизационных методов.

Примеры задач линейного программирования.

1.Задача об использовании ресурсов.

Для изготовления двух видов продукции Р₁ и Р₂ используется четыре вида ресурсов S₁, S₂, S₃, S₄. Запасы ресурсов, число единиц ресурсов, затрачиваемых на изготовление единицы продукции, приведены в таблице 1.

Таблица 3.

Вид ресурса	Запас ресурса	Число единиц ресурсов, затрачиваемых на изготовление единицы продукции
		Р1	Р2
S1	18	1	3
S2	16	2	1
S3	5	-	1
S4	21	3	-

Прибыль, получаемая от единиц продукции Р₁ и Р₂, известна и составляет соответственно 2 и 3 рубля.

Требуется составить такой план производства продукции, при котором прибыль от ее реализации будет максимальной.

Решение. Составим экономико-математическую модель задачи.

Пусть х₁ – число единиц продукции Р₁, и х₂ – число единиц продукции Р₂, запланированных к производству. Для их изготовления потребуется (1х₁+3х₂) единиц ресурса S₁, (2х₁+1х₂) единиц ресурса S₂, (1х₂) единиц ресурса S₃ и (3х₂) единиц ресурса S₄. Исходя из условия потребление ресурсов S₁, S₂, S₃, S₄ не должно превышать имеющихся запасов: 18, 16, 5 и 21 единицы. Тогда связь между потреблением ресурсов и их запасами выразится системой неравенств:

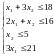(1)

Так как нельзя производить отрицательное количество продукции, то переменные:

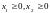(2)

Суммарная прибыль z составит 2х₁ рублей от реализации продукции Р₁ и 3х₂ рублей от реализации продукции Р₂. Составим целевую функцию:

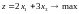(3)

В результате получили экономико-математическую модель задачи: найти такой план выпуска продукции Х=(х₁,х₂), удовлетворяющий системе (1) и условию (2), при котором функция (3) принимает максимальное значение.