Литература:

1. Исследование операций в экономике / п/р Н.Ш Кремера. – М.: ЮНИТИ, 2000. – 407с.

2. Вентцель Е.С. Исследование операций. Задачи, принципы, методология – М.: Наука, 1980.

Интернет – ресурсы:

1. Справочные материалы по высшей математике http://primat.at.ua

2. Электронные учебные пособия http://book.ru-deluxe.ru

Лекция 2. Модель межотраслевого баланса в. Леонтьева. План.

1. Условия и обозначения модели.

2. Матричный вид модели.

3. Критерий продуктивности.

Модель многоотраслевой экономики была разработана американским экономистом Василием Леонтьевым в 1936 году.

Модель Леонтьева это макроэкономическая модель и связана с ведением многоотраслевого хозяйства. В модели рассматривается многоотраслевая экономика (n отраслей). Целью построения модели Леонтьева является выяснение объема производства каждой из n отраслей производства, который бы удовлетворял все потребности в продукции этой отрасли. Каждая отрасль не только производит продукцию, но и потребляет продукцию, произведенную в этой же отрасли и в других отраслях производства.

Как уже было сказано ранее, рассматривается n отраслей экономики. Часть произведенной продукции идет на внутреннее потребление самой отраслью и другими отраслями, а другая (конечная) предназначена для личного и общественного потребления.

В модели рассматривается период в один год.

Введем следующие обозначения:

- общий (валовой объем) i-ой отрасли производства. i=1,2,…n;

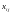- объем продукции, произведенной i-ой отраслью и потребляемой j-ой отраслью;

- объем конечного продукта i-ой отрасли.

Так как валовой объем продукции i-ой отрасли равен суммарному объему продукции, потребляемой n отраслями, в том числе и самой i-ой отраслью, и конечного продукта, то:

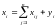
Будем называть это уравнение соотношением баланса.

Рассмотрим модель в стоимостном выражении. Для этого введем коэффициенты прямых затрат (КПЗ):

, где j меняется от 1 до n.

КПЗ показывает затраты i-ой отрасли на производство единицы продукции j-ой отрасли. В рассматриваемом промежутке времени КПЗ считается постоянной величинйо. Таким образом, материальные затраты и валовой выпуск имеют линейную зависимость:

.

Подставим данное выражение в соотношение баланса и оно примет вид:

Введем обозначения:

- вектор валового выпуска;

- вектор конечного продукта;

- матрица прямых затрат.

Запишем систему соотношений баланса в матричном виде:

Основная задаче межотраслевого баланса состоит в отыскании такого вектора валового выпуска Х, который, при известной матрице прямых затрат А, обеспечивает заданный вектор конечного продукта.

Преобразуем матричное уравнение. Перепишем его в следующем виде:

.

Если матрица (Е-А) вырожденная, то модель построена не верно, если же не вырожденная, то есть , то

.

Матрица называется матрицей полных затрат. - элемент матрицы показывает величину валового выпуска продукции i-ой отрасли, необходимую для обеспечения выпуска единицы конечного продукта j-ой отрасли.

Переменные , и в соответствии с экономическим смыслом задачи.

Матрица называется продуктивной, если для любого вектора конечного продукта существует решение – вектор валового выпуска 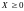матричного уравнения. Тогда и сама модель Леонтьева называется продуктивной.

Критерий продуктивности матрицы А:

Все элементы матрицы и (сумма по столбцам) и существует j для которого выполнено .

Пример 4

В таблице приведены данные об использовании баланса за отчетный период (в условных денежных единицах):

Таблица 1

Отрасль		Потребление		Конечный продукт	Валовой выпуск
		Энергетика	Машиностроение
Производство	Энергетика	7	21	72	100
	Машиностроение	12	15	123	150

Необходимо вычислить объем валового выпуска каждой отрасли, если конечное потребление энергетической отрасли увеличится вдвое, а машиностроения сохранится на прежнем уровне.

Решение.

Введем переменные соответственно модели. Из денных условий:

Найдем коэффициенты прямых затрат по формуле :

Матрица прямых затрат примет вид . Она имеет неотрицательные элементы и удовлетворяет критерию продуктивности, так как:

А это значит, для любого вектора конечного продукта Y можно найти необходимый объем валового выпуска Х по формуле:

Найдем матрицу полных затрат

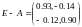
Определитель матрицы , отличен от нуля, то .

По условию вектор конечного продукта изменится и станет равным , тогда вычислим вектор валового выпуска