Литература:

1. Назаров М.Г., Варагин В.С. и др. // Статистика: учебно-практическое пособие. – М. КНОРУС, 2008. – 480 с.

2. Кремер Н.Ш. // Теория вероятностей и математическая статистика. – М.: ЮНИТИ-ДАНА, 2010. -551 с.

3. Майданюк Л.Н. //Статистика: сборник задач для практических занятий и методические рекомендации по их выполнению. – М.:МУПК, 1999. – 43 с.

Интернет – ресурсы:

1. Справочные материалы по высшей математике http://primat.at.ua

2. Электронные учебные пособия http://book.ru-deluxe.ru

Лекция №18:Статистические методы изучения взаимосвязей между социально-экономическими явлениями. Уравнения регрессии. План лекции.

1. Регрессионный анализ.

2. Виды регрессии.

3. Пример составления уравнения взаимосвязи в Excel.

4. Пример составления отчета.

Основная задача регрессионного анализа состоит в исследовании зависимости изучаемой переменной от различных факторов и отображении их взаимосвязи в виде регрессионной модели. Если объясняющий фактор один, то регрессия называется парной. Если объясняющих факторов больше, то регрессия называется множественной.

Величина Y называется объясняемой (зависимой) переменной, а X – объясняющей (независимой) переменной. Связь между переменными можно охарактеризовать как функцию регрессии.

Наиболее распространенной является линейная регрессия 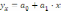, когда связь между переменными представлена в виде прямой линии. В качестве нелинейной регрессии может быть использована любая математическая функция.

Виды нелинейной регрессии:

1. Гипербола ;

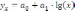2. Парабола 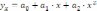(или другой ее степенью);

3. Степенная функция .

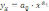Параметр показывает усредненное влияние на результативный признак неучтенных (не выделенных для исследования) факторов.

Параметр - коэффициент регрессии, показывает, на сколько измениться в среднем значение результирующего признака при увеличении независимого фактора на единицу.

Коэффициенты регрессии определяются методом наименьших квадратов. Для линейной связи составляется система уравнений:

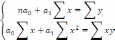
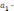Решив данную систему уравнений, найдем и для уравнения линейной регрессии .

Для степенной функции коэффициенты регрессии определяются так же методом наименьших квадратов. Система уравнений примет следующий вид:

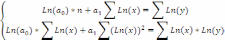
Решив систему уравнений, получим:

Приведем его в вид :

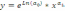
Пример 28.

По данным о стоимости основных производственных фондов и объеме валовой продукции определить уравнение связи и тесноту связи. Связь предполагается линейной.

Стоимость основных фондов	Объем валовой продукции
1	20
2	25
3	31
4	31
5	40
6	56
7	52
8	60
9	60
10	70

Решение.

Выполним по таблице следующие расчеты:

Стоимость основных фондов Х	Объем валовой продукции У	ХУ	Х^2
1	20	=B2*C2	=B2*B2
2	25	=B3*C3	=B3*B3
3	31	=B4*C4	=B4*B4
4	31	=B5*C5	=B5*B5
5	40	=B6*C6	=B6*B6
6	56	=B7*C7	=B7*B7
7	52	=B8*C8	=B8*B8
8	60	=B9*C9	=B9*B9
9	60	=B10*C10	=B10*B10
10	70	=B11*C11	=B11*B11
=СУММ(B2:B11)	=СУММ(C2:C11)	=СУММ(D2:D11)	=СУММ(E2:E11)

Найдем n как количество строк таблицы: =ЧСТРОК(B2:B11).

Все коэффициенты системы уравнений известны. Решим систему по формулам Крамера.

Запишем основную матрицу системы:

∆	=B14	=B12
	=B12	=E12

Найдем ее определитель:

∆	=B14	=B12	=МОПРЕД(B16:C17)
	=B12	=E12

Аналогично найдем ∆_х и ∆_у

∆х	=C12	=B12
	=D12	=E12	=МОПРЕД(B19:C20)
∆у	=B14	=C12
	=B12	=D12	=МОПРЕД(B22:C23)

Вычислим значения и :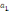

а0	=D20/D16
а1	=D23/D16

Получили коэффициенты уравнения связи .

Теперь можно рассчитать значения

Ун

=$B$25+$B$26*B2

=$B$25+$B$26*B3

=$B$25+$B$26*B4

=$B$25+$B$26*B5

=$B$25+$B$26*B6

=$B$25+$B$26*B7

=$B$25+$B$26*B8

=$B$25+$B$26*B9

=$B$25+$B$26*B10

=$B$25+$B$26*B11

=СУММ(F2:F11)

Теснота связи определяется по формуле корреляции:

Корреляция

=КОРРЕЛ(B2:B11;C2:C11)

Проверим правильность выполнения работы, воспользовавшись функцией =линеен, задав соответствующие параметры:

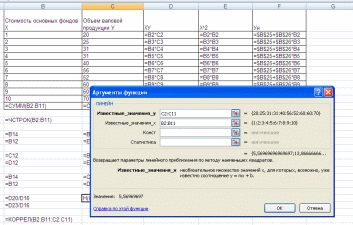
Важно.   Формулу в этом примере необходимо ввести как формулу массива. После введения формулы выделите диапазон из двух ячеек, начиная с ячейки, содержащей формулу. Нажмите клавишу F2, а затем — клавиши CTRL + SHIFT + ВВОД.

Получим те же самые результаты.