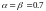Литература.

1. Исследование операций в экономике / п/р Н.Ш Кремера. – М.: ЮНИТИ, 2000. – 407с.

2. Орлова И.В., Половников В.А. Экономико-математические методы и модели: компьютерное моделирование: Учеб. Пособие – М., Вузовский учебник, 2007. – 365 с.

3. Просветов Г.И. Математические модели в экономике: Учебно-методическое пособие. - М.: Издательство РДЛ, 2005.

4. Интернет – ресурсы:

1. Справочные материалы по высшей математике http://primat.at.ua

2. Электронные учебные пособия http://book.ru-deluxe.ru

Лекция 13. Элементы теории игр. План.

1. Основные определения теории игр.

2. Парные игры.

3. Платежная матрица. Верхняя и нижняя цены игры.

4. Седловая точка.

5. Смешанные стратегии.

6. Решение игр в смешанных стратегиях.

До сих пор рассматривались модели, в которых были представлены интересы только одного субъекта. Но на практике часто возникают ситуации, когда две или более сторон преследуют различные цели, а результаты действий каждой из сторон зависят от мероприятий партнера. Так, например, знакомые всем игры в шашки, шахматы, карты относятся к конфликтным. Результат каждого хода игрока зависит не только от действий самого игрока, но и от ответного хода противника, цель игры для каждого - выигрыш.

В экономике конфликтные ситуации встречаются часто и имеют многообразный характер. К ним относятся, например, взаимоотношения между продавцами и покупателями, поставщиками и потребителями, банком и клиентом. Под конфликтными ситуациями будем понимать процессы, когда участники преследуют разные, зачастую противоположные цели.

Любой участник конфликта стремиться принимать оптимальное для себя решение, и при этом сталкивается не только со своими целями, но и с целями партнера, и зависит от решений, которые будет принимать партнер.

Методы для решения задач с конфликтной ситуацией разработаны в математической теории, которая называется теорией игр.

Основные понятия теории игр:

Игра - математическая модель конфликтной ситуации.

Игроки - стороны, участвующие в конфликте.

Выигрыш - исход конфликта.

Для любой формализованной игры вводятся правила, которые определяют:

1. варианты действия игроков;

2. объем информации каждого игрока о поведении партнера;

3. выигрыш, к которому приводит каждая совокупность действий.

В математических моделях выигрыш или проигрыш задается количественно.

Если выигрыш имеет качественный смысл, то ему в соответствие ставиться количественное значение. Например, игра в прятки. Выигрыш можно оценить как 1; проигрыш, как 0; а ничью, как 1/2.

Игра называется парной, если в ней участвуют два игрока. Игры с числом игроков больше двух называется множественными.

Мы будем рассматривать парные игры.

Пусть имеются два игрока: А и В и их интересы противоположны. Игра - это осуществлении ряда действий игроками А и В.

Игра называется игрой с нулевой суммой или антагонистической, если интересы партнеров противоположны, то есть выигрыш одного игрока равен проигрышу другого.

а - выигрыш игрока А;

в - выигрыш игрока В, тогда

а=-в.

В этом случае достаточно рассматривать только а, выигрыш игрока А, поскольку он же определяет проигрыш игрока В.

Ходом игрока называется выбор и осуществление одного из предусмотренных правилами действий.

Личный ход - это сознательный выбор игроком одного из возможных действий (например, ход в шахматах).

Случайный ход - случайно выбранное действие (например, выбор карты из колоды).

Стратегия игрока - это совокупность правил, определяющих выбор игрока при любом личном ходе, в зависимости от ситуации.

Бывает, что все решения игрока, в каждой сложившейся ситуации, приняты заранее. Это означает, что у игрока есть определенная стратегия, которая может быть задана в виде списка правил или программы. (Именно таким образом и пишутся многие компьютерные игры).

Игра называется конечной, если игрок имеет конечное число стратегий. В противном случае игра называется бесконечной.

Решение игры - это выбор каждым игроком стратегии, которая удовлетворяет условию оптимальности. Условие оптимальности означает что, если один игрок должен получить максимальный выигрыш, когда другой игрок придерживается своей стратегии, то в тоже время другой игрок должен иметь минимальный проигрыш, если первый придерживается своей стратегии. Такие стратегии называются оптимальными.

Условие устойчивости: каждому из игроков должно быть не выгодно отказаться от своей стратегии. Оптимальная стратегия должна удовлетворять условию устойчивости.

При многократно повторяющихся играх игроков интересует выигрыш или проигрыш в среднем.

Целью теории игр является определение оптимальной стратегии каждого игрока.

При выборе оптимальной стратегии предполагается, что оба игрока ведут себя разумно сточки зрения своих интересов. Важнейшее ограничение теории игр - единственность выигрыша, как показателя эффективности. Многие задачи в экономике имеют более одного показателя эффективности. Кроме того, в экономике, случаются ситуации, в которых интересы партнеров не антагонистические

Платежная матрица. Верхняя и нижняя цена игры.

Рассмотрим парную конечную игру. В этой игре игрок А имеет m стратегий A₁, A₂,…,A_m, а игрок В имеет n стратегий B₁, B₂,…,B_n.

Размерность такой игры будет mn.

В результате выбора игроками любой пары стратегий A_i и B_j (i=1,2,…m; j=1,2,…n) однозначно определяется исход игры, то есть выигрыш игрока А a_ij и проигрыш игрока В -a_ij.

Матрица P=(a_ij) (i=1,2,…m; j=1,2,…n), элементами которой являются выигрыши игрока А, которые соответствующие стратегиям A_i и B_j, называется платежной матрицей или матрицей игры. Платежная матрица имеет вид:

Таблица 15

	B1	B2	…	Bn
A1	a11	a12	…	a1n
A2	a21	a22	…	a2n
…	…	…	…	…
Am	am1	am2	…	amn

Строки платежной матрицы соответствуют стратегиям игрока А, а столбцы - стратегиям игрока В.

Пример 20

Игра "Поиск"

Игра заключается в том, что игрок А может спрятаться в одном из убежишь I или II, игрок В ищет игрока А. Если найдет, то получает от игрока А $1, если не найдет, то сам платит игроку А $1.

Игрок А имеет две стратегии:

А₁ - игрок А прячется в убежище I;

А₂ - игрок А прячется в убежище II.

Две стратегии имеет и игрок В:

В₁ - игрок В ищет в убежище I;

В₂ - игрок В ищет в убежище II.

Если игрок А в убежище I и В его обнаружил (стратегия A₁B₁), то игрок А платит игроку В $1 (а₁₁=-1). Аналогично для стратегии A₂B₂ а₂₂=-1.

Если А в убежище I, а В его не обнаружил (стратегия A₁B₂), то игрок А получает $1 (а₁₂=1). Аналогично для стратегии A₂B₁ а₂₁=1.

Размерность игры 22.

Платежная матрица игра, будет иметь тот же размер, что и игра 22:

-1	1
1	-1

Рассмотрим игру mn с платежной матрицей Р=(а_ij) размером mn.

Определим наилучшую стратегию игрока А среди стратегий A₁, A₂,…,A_m.

Выбирая стратегию А_i, игрок А рассчитывает, что В выберет стратегию В_j, для которой выигрыш игрока А будет минималным (игрок В вредит А).

Обозначим - минимальный выигрыш игрока А, при выборе им стратегии A_i, для всех возможных стратегиях В.

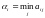- минимальное число в i-ой строке платежной матрицы.

Среди всех возможных выберем самое большое:

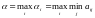
_{Полученный результат α назовем нижней ценой игры (максимин). Это} максимальный гарантированный выигрыш игрока А. Стратегия, соответствующая максимину называется максиминной стратегией.

Игрок В заинтересован в том, чтобы уменьшить свой проигрыш, равный выигрышу игрока А. Выбирая стратегию В_j, игрок В рассматривает при этом максимально возможный выигрыш игрока А. Обозначим его β_j.

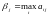- самый большой элемент в столбце j.

Среди всех возможных β_j игрок В будет стараться выбрать минимальный.

- верхняя цена игры (минимакс) - минимальный гарантированный проигрыш игрока В.

Стратегия, соответствующая минимаксу называется минимаксной стратегией.

Принцип, диктующий игрокам выбор "осторожных" минимаксных или максиминных стратегий называется принципом минимакса.

Найдем верхнюю и нижнюю цену игры "Поиск".

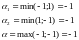
Следовательно, игрок А может выбирать любую стратегию А₁ или А₂, они обе масиминны. Нижняя цена игры равна -1.

Любая стратегия игрока В минимаксна и верхняя цена игры равна 1.

Если верхняя цена игры равна нижней цене игры, то 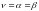- называется чистой ценой игры. Минимаксные стратегии, соответствующие чистой цене игры, называются оптимальными, а их совокупность - оптимальным решением или решением игры. Игрок А получает гарантированный, не зависящей от стратегии игрока В выигрыш , а игрок В добивается минимального гарантированного, не зависящего от выбора А, проигрыша .

Решение игры устойчиво: если один из игроков придерживается оптимальной стратегии, то для другого не может быть выгодным отклоняться от своей оптимальной стратегии.

Пара чистых стратегий A_i B_j дает оптимальное решение игры тогда и только тогда, когда a_ij - максимум в своем столбце и минимум в своей строке. Такая ситуация, если она существует, называется седловой точкой.

Пусть А^* В^* - пара чистых стратегий при которых достигается решение игры в задаче с седловой точкой. Введем функцию выигрыша игрока. P(A_i,B_j)=a_ij. Тогда, из условия оптимальности в седловой точке выполняется неравенство P(A_i,B^*) P(A^*,B^*) P(A^*,B_j), которое справедливо для всех i=1,2,…m; j=1,2,…n.

Пример 21

Найти верхнюю и нижнюю цену игры.

0,5	0,6	0,8
0,9	0,7	0,8
0,7	0,6	0,6

Имеет ли игра седловую точку?

Решение:

Найдем минимальные элементы в каждой строке и запиши их в столбец α_i. Найдем максимальные элементы в каждом столбце и запишем их в строку β_j.. Среди минимумов найдем максимум max(0,5;0,7;0,6)=0,7 Минимксная стратегия А₂. Среди максимумов найдем минимум min(0,9;0,7;0,8)=0,7 Максиминная стратегия В₂.

	В1	В2	В3
А1	0,5	0,6	0,8	0,5
А2	0,9	0,7	0,8	0,7
А3	0,7	0,6	0,6	0,6
	0,9	0,7	0,8

Таким образом , значит, игра имеет седловую точку а₂₂, и соответствующие ей стратегии А₂В₂ (решение игры) и чистая цена игры при этом .

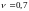Решение игр в смешанных стратегиях.

Если игра не имеет седловой точки, то применение чистых стратегий не дает оптимального решения игры. Оптимальное решение, в таком случае, можно получить, случайным образом чередуя чистые стратегии.

Смешанной стратегией S_A игрока А называется применение чистых стратегий А₁, А₂,…,А_i,…А_m с вероятностями p₁, p₂,…,p_i,…p_m, причем сумма вероятностей равна 1: .

Смешанные стратегии игрока записываются в виде матрицы:

,

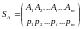или в виде строки .

Аналогично определяются смешанные стратегии игрока В. Они обозначаются:

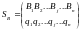или 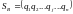, где сумма вероятностей появления стратегий игрока В равна 1: .

Чистые стратегии можно считать частным случаем смешанных стратегий и задавать строкой из нулей и единицы, причем единица должна стоять в позиции, соответствующей чистой стратегии. То есть одна чистая стратегия входит в смешанную с вероятностью 1, а остальные с вероятностью 0.

Оптимальное решение игры определяется на основании принципа минимакса: это пара оптимальных стратегий , в общем случае смешанных, которые обладают таким свойством, что один из игроков придерживается своей оптимальной стратегии, то другому не может быть выгодно отступать от своей оптимальной стратегии.

Выигрыш, соответствующей оптимальному решению, называется ценой игры . Цена игры удовлетворяет неравенству:

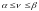, где - нижняя цена игры; - верхняя.

Теорема Неймана: каждая конечная игра имеет, по крайней мере, одно оптимальное решение, возможно, среди смешанных стратегий.

Активной называется чистая стратегия, которая входит в оптимальную смешанную стратегию с вероятностью, отличной от нуля.

Теорема об активных стратегиях: если один из игроков придерживается своей оптимальной смешанной стратегии, то выигрыш остается неизменным и равен цене игры , если второй игрок при этом не выходит за пределы своих активных стратегий.

Воспользуемся теорема об активных стратегиях и найдем оптимальные стратегии при отсутствии седловой точки.

Пусть задана платежная матрица игры:

Средний выигрыш игрока А, если он использует оптимальную смешанную стратегию

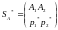, а игрок В чистую стратегию 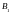(соответствует первому столбцу платежной матрицы Р), равен цене игры :

.

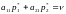Если игрок В выберет стратегию , то игрок А же получит средний выигрыш: 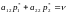. Учитывая, что 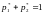, получим систему линейных уравнений, решив которую, определим оптимальную стратегию 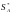и цены игра :

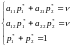
Решая эту систему методом исключения, получим оптимальную стратегию и цену игры:

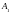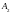Применив теорему об активных стратегиях для игрока В, получаем, что при любой чистой стратегии игрока А ( или ) средней проигрыш игрока В равен цене игры :

Получим систему линейных уравнений:

Решив ее, получим оптимальную стратегию игры (цена игры была определена при поиски оптимальной стратегии игрока А):

Пример 22

Игра "Поиск" задана платежной матрицей. Было показано, что эта матрица седловой точки не имеет:

Найдем решение игры «Поиск» в смешанных стратегиях; для игрока А средней выигрыш равен цене игры , для игрока В средний проигрыш равен цене игры . Системы уравнений имеет вид:

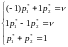
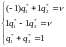
Решая эти системы получаем

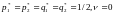
Это означает, что оптимальная стратегия каждого игрока состоит в том, чтобы чередовать свои чистые стратегии случайным образом, выбирая каждое из убежищ с вероятностью 1/2, при этом средней выигрыш равен 0.