
- •Оглавление
- •Введение
- •Лекция 1 Введение в математические методы. План.
- •Литература:
- •Интернет – ресурсы:
- •Лекция 2. Модель межотраслевого баланса в. Леонтьева. План.
- •Задание.
- •Литература.
- •Интернет – ресурсы:
- •Лекция 3. Предмет и задачи исследования операций. План.
- •Литература.
- •Интернет – ресурсы:
- •Лекция 4. Основные понятия линейного программирования. План.
- •Примеры задач линейного программирования.
- •1.Задача об использовании ресурсов.
- •Задача составления рациона (задача о диете, задача о смесях).
- •Общая задача линейного программирования.
- •Задания:
- •Интернет – ресурсы:
- •Лекция 5. Геометрический смысл решений неравенств и их систем неравенств. План.
- •Литература.
- •Интернет – ресурсы:
- •Лекция 6. Графический метод решения Задачи линейного программирования.
- •Литература.
- •Интернет – ресурсы:
- •Лекция 7. Особые случаи задач линейного программирования (графический метод). План.
- •Не единственность оптимального решения.
- •Лекция 8. Системы m линейных уравнений с n неизвестными.
- •Литература.
- •Интернет – ресурсы:
- •Лекция 9. Основы симплекс - метода линейного программирования План.
- •Алгоритм симплекс - метода:
- •Лекция 10. Метод искусственных переменных (м-метод).
- •Лекция 11. Теория двойственности.
- •Свойства взаимно двойственных задач.
- •Алгоритм составления двойственных задач.
- •Объективно обусловленные оценки и их смысл.
- •Лекция 12. Транспортная задача.
- •Определение транспортной модели
- •Пример транспортной модели
- •Приведение любой транспортная модель к сбалансированной.
- •Нахождение первоначального допустимого базисного решения.
- •I. Метод северо-западного угла
- •II.Метод минимальной стоимости.
- •Задания.
- •Литература.
- •Интернет – ресурсы:
- •Лекция 13. Элементы теории игр. План.
- •Задания:
- •Литература.
- •Интернет – ресурсы:
- •Лекция 14. Нелинейное программирование.
- •Лекция 15. Задача потребительского выбора.
- •Литература.
- •Интернет – ресурсы:
- •Лекция 16. Модели сетевого планирования и управления. План.
- •Задания.
- •Литература.
- •Интернет – ресурсы:
- •Лекция №17:Средние величины. Показатели вариации. План лекции.
- •Литература:
- •Интернет – ресурсы:
- •Лекция №18:Статистические методы изучения взаимосвязей между социально-экономическими явлениями. Уравнения регрессии. План лекции.
- •Литература:
- •Интернет – ресурсы:
- •Литература. Основная литература.
- •Дополнительная литература.
- •Интернет – ресурсы:
II.Метод минимальной стоимости.
Метод минимальной стоимости отличается от метода северо-западного угла тем, что на каждом шаге выбирается переменная не в верхней левой ячейке, а в ячейке, стоимость которой минимальна. Все дальнейшие действия осуществляются аналогично методу северо-западного угла.
Пример 19
|
5 |
15 |
15 |
10 |
||||
15 |
х11 |
10 |
х12 |
0 |
х13 |
20 |
х14 |
11 |
25 |
х21 |
12 |
х22 |
7 |
х23 |
9 |
х24 |
20 |
5 |
х31 |
0 |
х32 |
14 |
х33 |
10 |
х34 |
18 |
Найдем начальное базисное решение методом минимальной стоимости.
Ячеек с наименьшей стоимостью равной
0 несколько. Возьмем любую из них, например
(1, 2). Ей соответствует переменной
.
Присвоим переменной значение равное
min(15;15)=15. Поскольку объем
производства равен объему спроса, то
вычеркивается первая строка и второй
столбец. Так как вычеркнуты одновременно
строка и столбец, то из вычеркнутых на
этом шаге ячейках выбирается ячейка с
минимальной стоимостью и соответствующей
переменной присваивается значение 0,
 .
Далее, в оставшейся таблице выбираем
ячейку с минимальной стоимостью. Это
ячейка (3, 1). Переменная
.
Далее, в оставшейся таблице выбираем
ячейку с минимальной стоимостью. Это
ячейка (3, 1). Переменная
 .
Вычеркиваем первый столбец и третью
строку. Снова одновременно вычеркнули
и строку и столбец, тогда положим
.
Вычеркиваем первый столбец и третью
строку. Снова одновременно вычеркнули
и строку и столбец, тогда положим
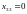 .
Осталось не вычеркнутыми две ячейки.
Соответственно присваиваем
.
Осталось не вычеркнутыми две ячейки.
Соответственно присваиваем
 .
Во втором пункте потребления остается
10 единиц. Переменной
.
Во втором пункте потребления остается
10 единиц. Переменной
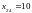 .
.
|
5 |
15 |
15 |
10 |
|
||||||||||
15 |
|
10 |
15 |
0 |
|
20 |
|
11 |
|
||||||
25 |
|
12 |
0 |
7 |
15 |
9 |
10 |
20 |
|||||||
5 |
5 |
0 |
|
14 |
0 |
10 |
|
18 |
|||||||
Получили начальное допустимое базисное решение:
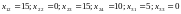
Целевая функция при этом будет равна:

Следует отметить, что значение целевой функции начального допустимого базисного решения найденного методом минимальной стоимости меньше, чем значение целевой функции начального допустимого базисного решения найденного методом северо-западного угла.
Критерий оптимальности и нахождение переменной вводимой в базис.
Метод потенциалов.
Метод потенциалов эквивалентен выражению целевой функции через небазисные переменные в обычном симплекс-методе.
Суть метода состоит в том, что каждому
столбцу i и каждой строке
j ставятся в соответствие
переменные
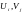 - потенциалы. Для потенциалов выполнено:
для всех базисных переменных
- потенциалы. Для потенциалов выполнено:
для всех базисных переменных
 .
Совокупность таких уравнений образует
систему m+n-1
уравнений с m+n
неизвестными. Значение потенциалов
определяется из этой системы, если
одному из потенциалов придается
произвольное значение. Обычно, потенциалу
U1 приписывается
значение 0. И из полученной системы
уравнений находят остальные потенциалы.
.
Совокупность таких уравнений образует
систему m+n-1
уравнений с m+n
неизвестными. Значение потенциалов
определяется из этой системы, если
одному из потенциалов придается
произвольное значение. Обычно, потенциалу
U1 приписывается
значение 0. И из полученной системы
уравнений находят остальные потенциалы.
Рассмотрим начальный допустимый план перевозок, найденный в примере 20:
|
V1 |
V2 |
V3 |
V4 |
||||
U1 |
5 |
10 |
10 |
0 |
|
20 |
|
11 |
U2 |
|
12 |
5 |
7 |
15 |
9 |
5 |
20 |
U3 |
|
0 |
|
14 |
|
10 |
5 |
18 |
Припишем каждой строке и каждому столбцу переменную – потенциал. Для ячеек с базисными переменными составим систему уравнений
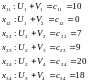
Найдем потенциалы. Положим
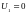 ,
тогда
,
тогда
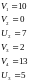
Далее, с помощью найденных потенциалов
получим оценки для небазисных переменных
по формуле:
 .
.
Получим оценки небазисных переменных для нашей задачи:

Критерий оптимальности: если все
оценки небазисных переменных
неположительные
 ,
то полученное решение оптимально.
,
то полученное решение оптимально.
Если критерий оптимальности не выполнен,
то переменная, имеющая самую большую
оценку, будет вводиться в базис. Если
таких несколько, то берем любую. В нашем
случае в базис должна быть введена
переменная
 .
.
Нахождение переменной, выводимой из базиса.
Этот шаг эквивалентен проверке условия допустимости в симплекс-методе. Увеличивать объем перевозки в клетке вводимой переменной (3;1) можно до тех пор, пока одна из базисных переменных не станет равной 0.
Распределительный метод (построение замкнутого цикла).
Для вводимой переменной строится замкнутый цикл (цикл начинается и заканчивается в ячейке вводимой переменной). Он состоит из вертикальных и горизонтальных перемещений по транспортной таблице, причем, смена направлений происходит только в ячейках с базисными переменными. Цикл всегда существует и всегда единственный.
|
5 |
15 |
15 |
10 |
||||
15 |
5 |
10 |
1 |
0 |
|
20 |
|
11 |
25 |
|
12 |
5(-) |
7 |
15 |
9 |
5(+) |
20 |
5 |
х31(+) |
0 |
|
14 |
|
10 |
5(-) |
18 |
Так как количество перевозимого груза
не измениться, то увеличение переменной
на 1 единицу эквивалентно уменьшению
переменной
 на 1 единицу, увеличению
на 1 единицу, увеличению
 на 1 единицу, уменьшению
на 1 единицу, уменьшению
 на 1 единицу, увеличению
на 1 единицу, увеличению
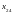 на 1 единицу, уменьшению
на 1 единицу, уменьшению
 на 1 единицу, то есть изменению всех
базисных переменных, стоящих в ячейках,
где цикл меняет направление.. Ячейки, в
которых перевозимая продукция увеличится,
пометим знаком "+", а в которых
уменьшиться - "-" (помечаются ячейки,
в которых меняется направление
построенного цикла). Начинаем с ячейки
вводимой переменной.
на 1 единицу, то есть изменению всех
базисных переменных, стоящих в ячейках,
где цикл меняет направление.. Ячейки, в
которых перевозимая продукция увеличится,
пометим знаком "+", а в которых
уменьшиться - "-" (помечаются ячейки,
в которых меняется направление
построенного цикла). Начинаем с ячейки
вводимой переменной.
Этот процесс всегда начинается на "+" и заканчивается на "-". Переменную, выводимую из базиса, будем искать в ячейках, помеченных знаком "-". Чтобы выполнилось условие допустимости выбирается переменная значение которой минимально. Эта переменная будет выводится из базиса.
После того как выводимая переменная найдена происходит переход к новой транспортной таблице. Он осуществляется по правилу: значение переменной, выводимой из базиса прибавляется ко всем значениям переменных, стоящих в ячейкам, помеченным знаком "+" и отнимается от значений переменных, стоящих в ячейках, помеченных "-".
В рассматриваемом примере min(5;5;5)=5. Следовательно, любую соответствующую переменную можно вывести из базиса. Возьмем переменную
|
5 |
15 |
15 |
10 |
||||
15 |
0 |
10 |
15 |
0 |
|
20 |
|
11 |
25 |
|
12 |
0 |
7 |
15 |
9 |
10 |
20 |
5 |
5 |
0 |
|
14 |
|
10 |
|
18 |
Значение целевой функции при этом уменьшилось на величину

После перехода к новой транспортной таблице, возвращаемся к шагу 2 и проверяем условие оптимальности с помощью метода потенциалов. Можно считать потенциалы по транспортной таблице, не выписывая отдельно систему. Оценки для небазисных переменных так же можно записать сразу в таблицу (они выделены жирным шрифтом).
|
V1=10 |
V2=0 |
V3=2 |
V4=13 |
||||
U1=0 |
0 |
10 |
15(+) |
0 |
-18 |
20 |
2 |
11 |
U2=7 |
х21(+) |
12 |
0(-) |
7 |
15 |
9 |
10 |
20 |
U3=-10 |
5 |
0 |
-24 |
14 |
-24 |
10 |
-15 |
18 |
Условие оптимальности снова не выполнено.
Находим переменную вводимую в базис.
Это х21, так как оценка 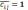 7
является наибольшей.
7
является наибольшей.
Построим замкнутый цикл и найдем переменную, выводимую из базиса. В ячейках, помеченных "-" обе переменные одинаковы и равны 0. Возьмем любую из них, например х11.
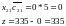
Значение целевой функции не изменилось. Продолжим решать задачу и перейдем к новой транспортной таблице:
|
V1=5 |
V2=0 |
V3=2 |
V4=13 |
||||
U1=0 |
-5 |
10 |
1 |
0 |
-18 |
20 |
х14(+) |
11 |
U2=7 |
0 |
12 |
0(+) |
7 |
15 |
9 |
10(-) |
20 |
U3=-5 |
5 |
0 |
-19 |
14 |
-13 |
10 |
-10 |
18 |
Критерий оптимальности вновь не выполнен.
В качестве вводимой переменной выбреем х14 , так оценка ячейки (1, 4) единственная положительная.
Построим замкнутый цикл, пометим ячейки смены направлений и выберем переменную, выводимую из базиса; ей будет х24.

Значение целевой функции уменьшиться. Продолжим решать задачу и перейдем к новой транспортной таблице:
|
V1=5 |
V2=0 |
V3=2 |
V4=11 |
||||
U1=0 |
-5 |
10 |
15 |
0 |
-18 |
20 |
10 |
11 |
U2=7 |
0 |
12 |
0 |
7 |
15 |
9 |
-2 |
20 |
U3=-5 |
5 |
0 |
-19 |
14 |
-13 |
10 |
-12 |
18 |
Во вновь полученной таблице критерий оптимальности выполнен. Транспортная задача решена. Ответ можно записать в форме таблицы.
|
5 |
15 |
15 |
10 |
15 |
х11=0 |
х12=15 |
х13=0 |
х14=10 |
25 |
х21=0 |
х22=0 |
х23=15 |
х24=0 |
5 |
х31=5 |
х32=0 |
х33=0 |
х34=0 |
Суммарная стоимость всех перевозок равна 315.
Примеры задач транспортной модели.
Модель производства за запасами
Рассмотрим применение транспортной модели в других социально-экономических сферах.
Пусть некоторая фирма переводит свой завод на производство определенного вида продукции, которая будет выпускаться в течение четырех месяцев. Планируемый спрос составит 100, 200, 180 и 300 единиц соответственно. В каждом месяце спрос может удовлетворяться за счет:
избытка производства в предыдущих месяцах;
производства в настоящее время;
избытка производства в последующем периоде в счет невыполненных заказов.
Стоимость производства единицы продукции составляет $4. Изделие, произведенное ранее, влечет затраты на хранение $0,5 в месяц. Штраф за невыполненный заказ составляет $2,8 в месяц. Объем производства составит 50, 180, 280, 270 изделий соответственно.
Задача заключается в составлении плана реализации и хранения товара, имеющего минимальную стоимость.
Проведем аналог с транспортной задачей:
Таблица 14
Транспортная задача |
Производство с запасами |
1. Исходный пункт i |
1. Период производства i |
2. Пункт потребления j |
2. Период реализации j |
3. Предложение в пункте i (ai) |
3. Объем производства в период i (ai) |
4. Спрос в пункте j (bj) |
4. Объем сбыта в период j (bj) |
5. Стоимость перевозок сij |
5. Стоимость производства и хранения сij |
Стоимость производства и хранения сij в модели производства с запасами равна:
затратам на производство в i-ом периоде (i=j);
затратам на производство в i-ом периоде и затратам на хранений в j-i периодах (j>i);
затратам на производство в i-ом периоде и штрафам в i-j периодах (j<i).
Составим транспортную таблицу задачи производства с запасами:
|
|
Потребление |
||||||||||
производство |
|
100 |
200 |
180 |
300 |
|||||||
50 |
х11 |
4 |
х12 |
4,5 |
х13 |
5 |
х14 |
5,5 |
||||
180 |
х21 |
6 |
х22 |
4 |
х23 |
4,5 |
х24 |
5 |
||||
280 |
х31 |
8 |
х32 |
6 |
х33 |
4 |
х34 |
4,5 |
||||
270 |
х41 |
10 |
х42 |
8 |
х43 |
6 |
х44 |
4 |
||||

 (-)
(-) 0(+)
0(+) (-)
(-) 5(-)
5(-)