Лекция 10. Метод искусственных переменных (м-метод).

План.

1. Невозможность нахождения первоначального базисного решения.

2. Искусственные переменные.

3. 2-х этапный симплекс метод.

Пример с использованием М-метода.

В рассматриваемой вычислительной схеме симплекс-метода для получения начального базисного решения используются дополнительные переменные. Допустимое базисное решение получается в случае, когда все ограничения вида "". В случае же, когда ограничений вида "" или "=" начальное базисное решение может быть недопустимым, то есть содержать отрицательные компоненты.

Существует специальный метод для получения системы в каноническом виде, обладающей допустимым базисным решением. Сначала задача линейного программирования приводится к канонической форме, все переменные в которой неотрицательные. Затем для каждого ограничения проверяется существование соответствующей допустимой базисной переменной (не отрицательной). Если ее нет, то вводится новая искусственная переменная y_j. Искусственная переменная вводится с тем же знаком, что и свободный член. Искусственных переменных столько, сколько ограничений дающих отрицательную компоненту в первоначальном базисе. Введенная искусственная переменная играет роль базисной переменной для данного ограничения. После проверки всех ограничений получается расширенная система в каноническом виде, которая имеет допустимое базисное решение, следовательно, можно заполнить начальную симплексную таблицу. Так как введенные переменные не имеют отношения к существу задачи линейного программирования в исходной постановке, то необходимо добиться обращения их в ноль. Для этого составим новую целевую функцию:

T=z-M(y₁+…+y_k), где

М – произвольное, большое по отношению к задаче число;

k – количество искусственных переменных, и ищем максимальное значение Т-функции.

Теорема:

1. Если в оптимальном решение Т-задачи все искусственные переменные равны 0, то соответствующие значения остальных переменных дают оптимальное решение исходной задачи линейного программирования.

2. Если имеется оптимальное решение Т-задачи, в котором хотя бы одна из искусственных переменных отлична от 0, то система ограничений исходной задачи линейного программировании несовместна.

3. Если максимум Т-функции равен бесконечности, то исходная задача неразрешима (либо система несовместна, либо максимум неограничен).

На практике, как правило, применяют двухэтапный симплекс-метод. Для этого Т-задачу разбивают на две задачи. Каждая из них решается на своем этапе.

1. Этап 1. Рассматривается искусственная целевая функция равная -M(y₁+…+y_k). Ее еще называют М-функция. При помощи симплекс-метода находят максимум М-функции. В результате поиска максимума производится исключение искусственных переменных. Если максимальное значение вспомогательной задачи равно нулю, то в ноль обращаются все искусственные переменные. Получается допустимое базисное решение начальной задачи линейного программирования, которая реализуется на этапе 2. Если минимальное значение вспомогательной задачи положительное, то по крайней мере одна из искусственных переменных также положительная. Это говорит о противоречивости начальной задачи, и решение прекращаются.

2. Этап 2. Допустимое базисное решение, найденное на первом этапе, улучшается с помощью алгоритма симплекс-метода. оптимальная таблица 1-го этапа становиться в начальной таблицей этапа 2.

Пример 13

Решить задачу линейного программирования:

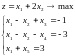
Базисное решение, получаемое на первом шаге X₁= (0; 0; -1; 3; 3) не является допустимым. В первое ограничение, дающее отрицательную компоненту, надо ввести искусственную переменную y₁. Переменная вводится с тем же знаком, что и свободный член. Получим систему:

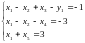
Преобразуем систему ограничений, так чтобы все свободные члены были неотрицательными. Для этого умножим первое и второе уравнение на –1. Получим:

Т-функция будет иметь вид: Т=x₁+2x₂-My₁max.

Заполним первую симплекс-таблицу:

Базис	Свободный член	Переменные						Оценочные отношения
		x1	x2	x3	x4	x5	y1
y1	1	-1	1	-1	0	0	1		1
x4	3	-1	1	0	1	0	0		3
x5	3	1	0	0	0	1	0		
z	0	-1	-2	0	0	0	0
Мф	-М	М	-М	М	0	0	0

Последняя строка таблицы – это (-М-функция), в нашем случае -My₁. Заполняется она путем выражения искусственных переменных через небазисные переменные. Строки, в которых присутствует искусственная переменная умножаются на –М и их соответствующие компоненты складываются (в нашем случае умножается первая строка). В качестве оценочной строки рассматривается строка М-функции, обозначенная М_ф. Критерий оптимальности проверяется по строке М-функции. Он не выполнен. Отрицательный коэффициент соответствует столбцу переменной х₂. Она вводится в базис. Считаем оценочные отношения и находим переменную, выводимую из базиса. Это переменная y₁. Переходим к новой симплекс таблице.

Базис	Свободный член	Переменные						Оценочные отношения
		x1	x2	x3	x4	x5	y1
х2	1	-1	1	-1	0	0	1
x4	2	0	0	1	1	0	1
x5	3	1	0	0	0	1	0
z	2	-3	0	-2	0	0	-2
Мф	0	0	0	0	0	0	М

По последней строке видно, что критерий оптимальности выполнен: максимальное значение М-функции равно нулю: max(-M_ф)=0. Искусственная переменная y₁. тоже равна нулю. Полученое базисное решение (0; 1; 0; 2; 3) является допустимым. Далее, переходим ко второму этапу. Отбросываем последнюю строку и столбец с искусственной переменной

Базис	Свободный член	Переменные					Оценочные отношения
		x1	x2	x3	x4	x5
х2	1	-1	1	-1	0	0
x4	2	0	0	1	1	0
x5	3	1	0	0	0	1
z	2	-3	0	-2	0	0

Задания.

Задачи 1-6 из раздела особые случаи симплекс-метода (графический метод) решить с помощью М-метода.

Литература.

1. Исследование операций в экономике / п/р Н.Ш Кремера. – М.: ЮНИТИ, 2000. – 407с.

2. Банди Б. Основы линейного программирования. – М.: Радио и связь, 1989.

3. Вентцель Е.С. Исследование операций. – М.: Сов. радио, 1972.

4. Горелик В.А., Ушаков И.А. Исследование операций. – М.: Машиностроение, 1986.

Интернет – ресурсы:

1. Справочные материалы по высшей математике http://primat.at.ua

2. Электронные учебные пособия http://book.ru-deluxe.ru