Лекция 8. Системы m линейных уравнений с n неизвестными.

План.

1. Системы с разным числом переменных и уравнений.

2. Базисные решения.

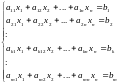
В задачах линейного программирования особый интерес вызывают системы линейных уравнений, в которых ранг (r) матрицы системы (A) меньше чем число переменных n.

В таких системах уравнений число переменных n больше числа независимых уравнений m (m<n).

Базисными или основными переменными системы уравнений с n переменными (m<n) называются любые m переменных, определитель матрицы коэффициентов которых отличен от нуля.

Неосновными или свободными называются остальные n-m переменных.

Максимально возможное число наборов базисных переменных равно .

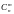Пример 9

Рассмотрим систему уравнений:

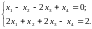
Так два уравнения, то и базисных переменных будет две. Максимально возможное число наборов базисных переменных равно:

Рассмотрим все возможные наборы базисных переменных: х₁х₂; х₁х₃; х₁х₄; х₂х₃; х₂х₄; х₃х₄.

Проверим, действительно ли все эти наборы переменных могут быть базисными.

Проверим набор переменных х₁х₂. Посчитаем определитель матрицы коэффициентов при этих перемен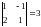ных: _. Определитель отличен от нуля, следовательно, переменные х₁х₂ можно выбрать в качестве базисных.

Проверим набор переменных х₄х₃. Посчитаем определитель матрицы коэффициентов при этих переменных: 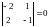_. Определитель равен нулю, а значит переменные х₂х₃ нельзя выбрать базисными.

Остальные наборы переменных проверьте самостоятельно.

Допустимым называется решение системы линейных уравнений X(x₁,x₂,…,x_n), у которого все компоненты неотрицательны ( ).

Если условие неотрицательности не выполнено хотя бы для одного компонента решения x_j, то решение системы называется недопустимым.

Базисным решением системы m линейных уравнений с n переменными называется такое решение, в котором неосновные переменные равны нулю.

Пример 10

Рассмотрим систему уравнений примера 9. Возьмем в качестве базисных переменных х₁х_2. Следовательно, в базисном решении переменные х₃х₄ будут равны 0. Получим:

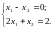
Решив полученную систему уравнений, найдем х₁=2/3, х₂=2/3.

А само базисное решение будет иметь вид: (2/3; 2/3; 0; 0).

Литература.

1. Исследование операций в экономике / п/р Н.Ш Кремера. – М.: ЮНИТИ, 2000. – 407с.

2. Высшая математика для экономистов / п/р Н.Ш Кремера. – М.: ЮНИТИ, 2002. – 471с.

Интернет – ресурсы:

1. Справочные материалы по высшей математике http://primat.at.ua

2. Электронные учебные пособия http://book.ru-deluxe.ru

Лекция 9. Основы симплекс - метода линейного программирования План.

1. Условия для применения симплекс- метода.

2. Пример решения задачи симплекс-методом.

3. Алгоритм симплекс-метода с использованием симплекс-таблицы.

4. Пример решения задачи табличным симплекс-методом.

Симплекс - метод представляет собой итеративную процедуру решения задач линейного программирования. Для решения задачи симплекс-методом она приводится к каноническому виду. Было доказано, что любую задачу линейного программирования можно привести к каноническому виду:

(1)

После приведения задачи к каноническому виду в ней будет n+m переменных.

В качестве базисных переменных на первом шаге выбирают дополнительные переменные. Их m штук и каждая из них входит с единичными коэффициентами только в одно уравнение системы и с нулевыми - в остальные (матрица коэффициентов – единичная матрица, ее определитель равен 1). В полученной канонической системе уравнений каждая базисная переменная входит только в одно уравнение (каждому уравнению системы соответствует ровно одна базисная переменная). Остальные n переменных называются небазисными переменными.

Будем считать, что решается задача на максимум (задачу на минимум можно свести к задаче на максимум, умножив целевую функцию на (-1))

Пример 11

Решим задачу симплекс-методом:

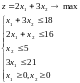
Приведем систему ограничений к каноническому виду и получим расширенную систему:

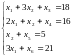
Для нахождения первоначального базисного решения разобьем переменные на основные и неосновные .Возьмем в качестве базисных переменных дополнительные переменные х₃, х₄ х₅ и х₆. Определитель матрицы коэффициентов при х₃, х₄ х₅ и х₆ отличен от нуля (каждая из этих переменных входит только в одно ограничение причем с коэффициентом 1, то есть матрица коэффициентов при них будет единичной). Переменные х₁ и х₂ будут неосновными.

Правило: на первом шаге в качестве основных переменных следует выбирать такие из них, которые входят только в одно из уравнений системы ограничений, при этом нет таких уравнений, в которое не входит ни одна их этих переменных.

Если дополнительные переменные имеют тот же знак что и свободные члены в правой части, то они удовлетворяют этом правилу.

1). Получим на первом шаге:

Базисные переменные	Не базисные переменные
х3, х4 х5 х6	х1 х2

Выразим небазисные переменные через базисные:

(*)

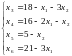Получим первое базисное решение системы ограничений Х₁=(0; 0; 18; 16; 5; 21). Если сравнить с графическим решением этой задачи, то Х₁ соответствует точке О(0;0) многоугольника ОАВСДЕ (см. рис. 1).

Это решение допустимое, поэтому нельзя исключать, что оно оптимальное.

Выразим целевую функцию через неосновные переменные: , z(X₁)=0.

Функцию z можно увеличить за счет неосновной переменной (обе они входят в уравнение с коэффициентом >0). Это можно осуществить, перейдя к новому допустимому базисному решению, в котором одна из этих переменных станет основной. Если новое решение будет вырожденным, то целевая функция сохранит свое значение. Геометрически это переход к другой соседней вершине, в которой целевая функция имеет по крайней мере не худшее. В рассматриваемой задаче можно переводить в базисные переменные как х₁ так и х₂, так как обе входят в целевую функцию со знаком «+».

Для определенности будем выбирать в такой ситуации переменную с наибольшим коэффициентом в целевой функции. В данной задаче это х₂.

Система ограничений (*) накладывает ограничения на рост х₂, так как необходимо сохранять допустимость решения (все переменные должны быть не меньше 0). Поэтому следующие неравенства должны быть выполнены при х₁=0:

Любое уравнение системы (*) (кроме последнего) определяет оценочное отношение – границу роста переменной х₂, сохраняющую неотрицательность соответствующей переменной. Эта граница определяется абсолютной величиной отношения свободного члена к коэффициенту при х₂, если они имеют разные знаки. Так как в последнее ограничение х₂ не входит (входит с коэффициентом 0), то рост х₂ не ограничен, х₂<∞. Будем так же считать, сто граница переменной х₂ равно ∞, если коэффициент перед х₂ и свободный член имеют одинаковые знаки. Нет ограничений на рост х₂ и в том случае, если свободные член равен 0. Но если при этом коэффициент при х₂ отрицательный, то рост этой переменной ограничен 0.

Так как неотрицательность должны сохранять все переменные, по новая базисная переменная х₂=min(6; 16; 5; ∞)=5. Уравнение, которое соответствует минимальной оценке, называется разрешающим. В этом примере – это третье уравнение

Следовательно, переменная х₅=0 и переходит в небазисные переменные.

2). Получим на втором шаге:

Базисные переменные	Не базисные переменные
х3, х4 х2 х6	х1 х5

Из третьего уравнения системы выразим :х₂:

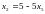
Подставляя правую часть равенства во все остальные уравнения вместо х₂ получим:

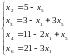
Получим новое базисное решение системы Х₂=(0; 5; 3; 11; 0; 21). Это соответствует точке А(0;5) многоугольника ОАВСДЕ (см. рис. 1).

Выразим целевую функцию через неосновные переменные: 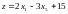, z(X₂)=15.

Аналогично рассуждениям, проведенным на первом шаге, сделаем вывод, что целевую функцию можно улучшить введя в базисные переменные х₁.

х₁=min(∞; 13; 11/2; ∞)=3, следовательно второе уравнение разрешающее и х₃ выводится из базиса.

3). Получим на третьем шаге:

Базисные переменные	Не базисные переменные
х1, х4 х2 х6	х3 х5

Из второго уравнения системы выразим :х₁:

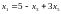
Подставляя правую часть равенства во все остальные уравнения вместо х₁ получим:

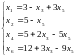
Получим новое базисное решение системы Х₃=(3; 5; 0; 5; 0; 12). Это соответствует точке В(3;5) многоугольника ОАВСДЕ (см. рис. 1).

Выразим целевую функцию через неосновные переменные: 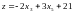, z(X₃)=21.

Аналогично первым двум шагам введем в базисные переменные х₅.

х₅=min(∞; 5; 1;4/3)=1, следовательно, третье уравнение разрешающее и х₄ выводится из базиса.

4). Получим на четвертом шаге:

Базисные переменные	Не базисные переменные
х1, х5 х2 х6	х3 х4

Из третьего уравнения системы выразим :х₅:

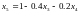
Подставляя правую часть равенства во все остальные уравнения, вместо х₅ получим:

Получим новое базисное решение системы Х₄=(6; 4; 0; 0; 1; 6). Это соответствует точке С(6;4) многоугольника ОАВСДЕ (см. рис. 1).

Выразим целевую функцию через неосновные переменные: , z(X₄)=24.

Целевую функцию нельзя улучшить переходя к другому базисному решению, так как все коэффициенты при небазисных переменных меньше 0, следовательно, задача решена. Максимальная прибыль при этом равна 24, а оптимальный план производства: 6 единиц первой продукции и 4 единицы второй продукции. Дополнительные переменные показывают разницу между затратами ресурсов каждого вида и их потреблением. х₃=х₄=0, следовательно ресурсы S₁ иS₂ расходуются полностью в процессе производства, а остатки S₃ иS₄ равны 1 и 3 соответственно.

На практике расчеты при решении задач симплекс-методом выполняются с помощью симплекс-таблиц. Рассмотрим алгоритм симплекс-метода с использованием симплекс-таблиц.