3 . Выпуклым многоугольником:

2x₁+x₂ ≥2

x₁+3х₂ ≥3

x₁-x₂ ≥-1

Зх₁-х₂ ≤ 6

x₁+x₂ ≤ 5

x₁≥0;х₂≥0

Рис. 1.6.5. ОДЗ — выпуклый многоугольник

4 . неограниченной выпуклой многоугольной областью:

Зх₁-2х₂ ≥-15

4х₁-х₂ ≥20

Зх₁+х₂ ≥30

x₁-2х₂ ≤20

х₁ ≥0;х₂ ≥0

Рис. 1.6.6. ОДЗ — неограниченная выпуклая многоугольная область

Н а втором этапе формируется графическое изображение целевой функции.

Уравнение: c₁x₁+c₂x₂ =L при фиксированном значении L определяет прямую, а при изменении L — семейство параллельных прямых с параметром L. Вектор С=(с₁ ,с₂), перпендикулярный всем этим прямым, показывает направление возрастания параметра L. Так, на рис. 1.6.7. показаны прямые, соответствующие уравнению 2x₁+3x₂=L при L= -3, 0, 3, 9.

Рис. 1.6.7. Графическое изображение целевой функции

Д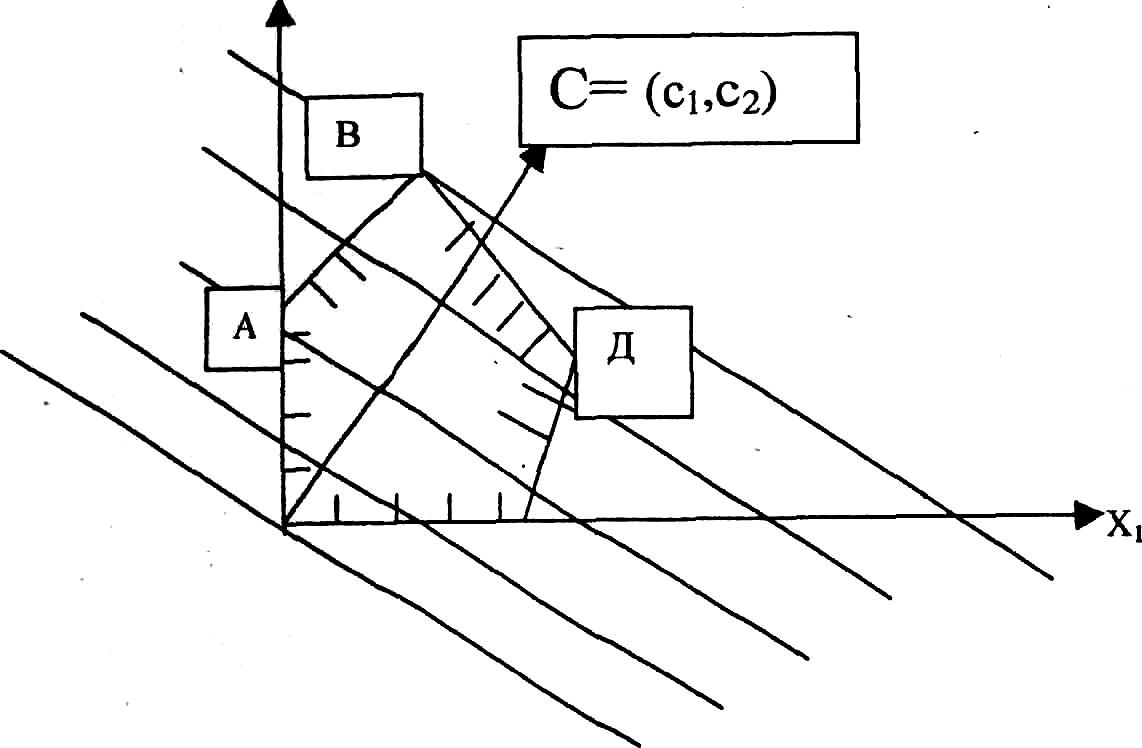 ля всех точек, лежащих на одной из этих прямых, функция F принимает одно определенное значение, равное соответствующему значению L. Поэтому рассматриваемые прямые называются линиями уровня для параметра L. Важное свойство линии уровня в том, что при их параллельном смещении в одном направлении уровень (значение L) только возрастает, а при смещении в другом — только убывает. Построим для рассмотренного примера линии уровня и определим направление их возрастания. Чтобы построить вектор C=(c₁, с₂), можно использовать следующий прием: по оси X₁ откладывается значение первой компоненты вектора C₁=2, а по оси Х₂ — значение второй компоненты С₂=3. По найденным координатам строим прямоугольник и находим направление возрастания вектора С. Затем перпендикулярно вектору С строим линии уровня.

Рис. 1.6.8. Определение оптимального решения графическим методом

Построив на одном рисунке (рис. 1.6.8) область допустимых решений, вектор С, и перпендикулярную ему одну из линий уровня, можно путем ее параллельного перемещения в направлении, указанном вектором С (или в противоположном), определить точку в области допустимых значений, которая доставляет максимум или минимум целевой функции. На рис. 1.6.8 видно, что в крайнем положении линия уровня проходит через (*)В. При дальнейшем ее перемещении она уже не будет иметь общих точек с областью допустимых решений. Таким образом, искомое оптимальное решение, которое графически соответствует координатам (*)В, можно найти путем совместного решения системы двух уравнений, соответствующих граничным прямым АВ и ВД. Если при тех же исходных данных требовалось бы достичь минимума функции F, то, очевидно, линию уровня пришлось бы перемещать в направлении, противоположном вектору С. В этом случае оптимальное решение, соответствующее минимуму функции F, определялось бы координатами точки (*)0.

В зависимости от вида области допустимых решений и положения линий уровня возможны следующие случаи:

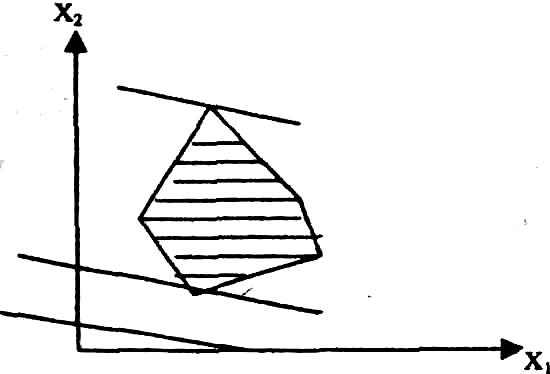
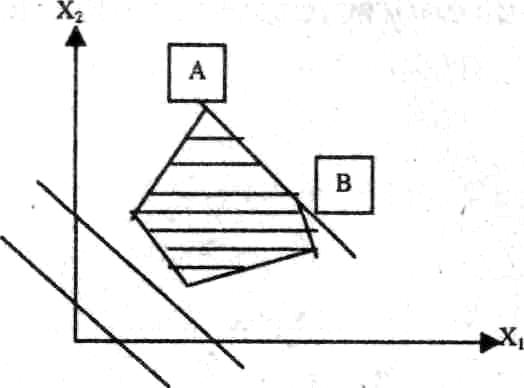
1.6.9. Злп имеет единственное решение 1.6.10. Злп имеет альтернат. Оптимум (а и в)

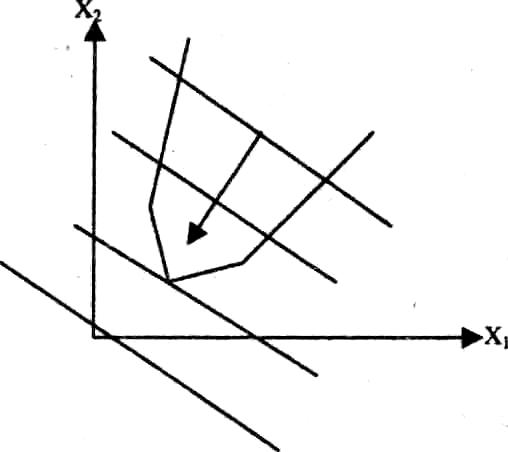
1.6.11. Злп имеет минимум и не имеет максимума 1.6.12. Злп не имеет решения

Область допустимых решений, изображенная на рис. 1.6.9 и 1.6.10, соответствует одной и той же системе неравенств:

2x₁+x₂ ≥2

х₁+3x₂ ≥3

х₁-х₂ ≥-1

3x₁-x₂ ≤6

х₁+х₂ ≤ 5

_Xl ≥0;x₂ ≥0, но функции, которые максимизируются, отличаются друг от друга:

• в первом случае — F=x₁+2x₂,

• во втором — F= х₁+x₂

Рассмотренные выше примеры показывают, что:

• оптимальное значение целевой функции в первом примере, графическое изображение которого представлено на рис. 1.6.9, достигается в одной единственной точке;

• оптимальное значение во втором примере, графическое изображение которого представлено на рис. 1.6.10, достигается в двух вершинах выпуклого многоугольника и, следовательно, в любой точке отрезка АВ, соединяющего эти две вершины. В этом случае задача имеет альтернативный оптимум, т.е. множество оптимальных решений. Произошло это потому, что линии уровня целевой функции оказались параллельны одной из сторон замкнутого выпуклого многоугольника, представляющего собой область допустимых решений;

• оптимальное значение целевой функции в третьем примере, графическое изображение которого представлено на рис. 1.6.11, где область допустимых решений представляет собой выпуклую неограниченную область, может существовать, если целевая функция стремится к минимуму, и не будет существовать, если целевая функция будет стремиться к максимуму;

• оптимальное значение целевой функции в четвертом примере, изображение которого представлено на рис. 1.6.12, где область допустимых решений представляет собой выпуклую неограниченную область, а целевая функция F оказывается не ограниченной ни сверху, ни снизу, — не существует.