6. Графический метод решения злп

Графический метод решения ЗЛП имеет ограниченную область применения. Как правило, этим методом решаются задачи, содержащие не более двух переменных.

Пример

Найти решение X*=(x*₁,x*₂), которое удовлетворяет системе неравенств:

a _llx₁+a₁₂x₂ ≤ b₁

a₂₁x₁+a₂₂x₂ ≤ b₂ (1.6.1)

а₃₁х₁+а₃₂х₂ ≤ b₃

_{…………………………………………}

a_m1х₁+а_m2х₂ ≤ b_m

условиям неотрицательности переменных:

х ₁ ≥ 0, х ₂ ≥ 0 (1.6.2)

и которое доставляет оптимальное значение целевой функции:

F = c₁x₁+c₂x₂ —>max(min). (1.6.3)

Применение геометрического метода предполагает использование нескольких этапов.

На первом из них в системе координат X₁OX₂ строится область допустимых решений задачи (ОДЗ). Для этого каждое из неравенств системы (1.6.1) заменяем равенством и строим соответствующие этим равенствам граничные прямые: a_ilx₁+a_i2x₂ = b_i (i=l,…, m).

Каждая из этих прямых делит плоскость Х₁ОХ₂ на две полуплоскости (рис. 1.6.1). Для точки (*) А, принадлежащей одной из этих полуплоскостей, выполняется неравенство: a_ilx₁+a_i2x₂ < b_i (i=l,…, m).

для любой (*)В, принадлежащей другой полуплоскости, — противоположное: a_ilx₁+a_i2x₂ > b_i (i=l...m),

а для любой из точек, лежащих на граничной прямой, — уравнение: a_ilx₁+a_i2x₂ = b_i (i=l.. .m).

Рис. 1.6.1. Построение ОДЗ

Чтобы графически определить, по какую сторону от граничной прямой располагается полуплоскость, содержащая решения, удовлетворяющие рассматриваемому неравенству, достаточно испытать одну какую-либо точку, например точку с координатами (0,0). Если при подстановке ее координат в левую часть неравенства оно удовлетворяется, значит, искомая полуплоскость содержит данную точку и штриховка, выделяющая искомую полуплоскость, обращена в сторону к испытуемой точке.

Если же неравенство не удовлетворяется, штриховка, выделяющая искомую полуплоскость, обращена в противоположную от данной точки сторону.

Неравенства x₁≥0 и х₂≥0 также соответствуют полуплоскостям, одна из которых расположена справа от оси ординат, а другая - над осью абсцисс (рис. 1.6.1).

Выделив полуплоскости, содержащие решения, удовлетворяющие неравенствам, входящим в рассматриваемую систему, мы определим область, в которой находятся решения, удовлетворяющие всем ограничениям, входящим в рассматриваемую систему неравенств. Именно эта область и есть область допустимых решений задачи.

Пример. Необходимо построить область допустимых решений, удовлетворяющую системе неравенств:

x₁+х₂≤ 1

x₁-x₂≤ -1

х ₁ ≥ 0, х ₂ ≥ 0

Для этого первое из неравенств обратим в равенство (x₁+х₂= 1) и построим соответствующую ему граничную прямую. Эта прямая проходит через две точки, координаты которых можно определить следующим образом. Положим, x₁=0, тогда получим 0+х₂= 1, т. е., х₂= 1,а если х₂=0, тогда x₁+0= 1, т. е.,x₁=l, следовательно, граничная прямая на рис. 1.6.2 проходит через точки с координатами (0,1) и (1,0).

Чтобы определить; в какой полуплоскости находят решения, удовлетворяющие первому неравенству, подставим точку с координатами (0,0) в первое неравенство 0+0≤ 1 и убедимся, что точка (0,0) ему удовлетворяет. Следовательно, все решения, удовлетворяющие данному неравенству, находятся в той же полуплоскости, что и точка 0, значит, штриховка, выделяющая полуплоскость, содержащую решения, удовлетворяющие первому неравенству, обращена к точке 0. Затем определим полуплоскость, в которой находятся решения, удовлетворяющие второму неравенству. Для этого второе из неравенств обратим в равенство и построим соответствующую этому равенству граничную прямую. С помощью приема, описанного выше, определим точки, через которые проходит граничная прямая; этими точками будут: (x₁=0, х₂=1) и (x₂=0, x₁=-l).

И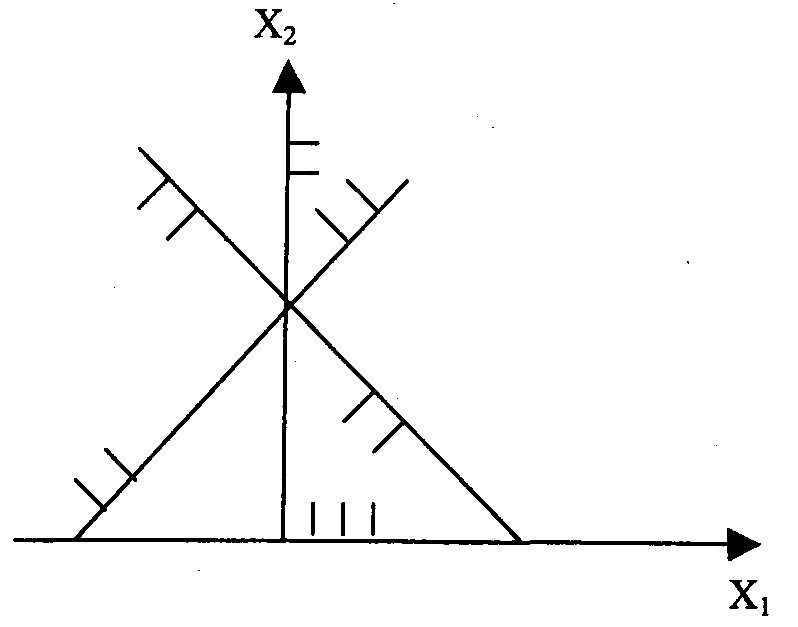 спытав точку 0, увидим, что штриховка, выделяющая полуплоскость, содержащую решения, удовлетворяющие первому неравенству, обращена в сторону, противоположную от 0.

Выделим полуплоскости, соответствующие неравенствам: x₁ ≥ 0 и х₂ ≥ 0. Полуплоскость справа от оси ординат будет соответствовать неравенству x₁ ≥ 0, а полуплоскость над осью абсцисс — неравенству х₂ ≥ 0. В рассматриваемом примере область допустимых решений состоит из одной точки с координатами (0,1). Рис. 1.6.2. ОДЗ —одна точка

В общем случае область допустимых решений систем неравенств (1.6.1) и (1.6.2) может быть:

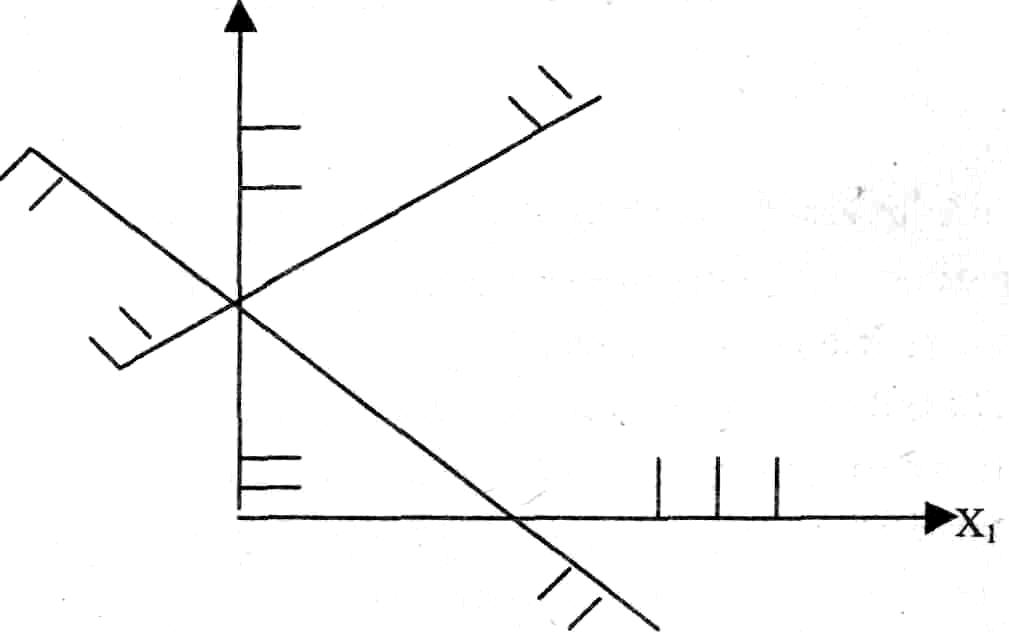
1. пустой, что означает несовместимость систем неравенств:

x ₁+x₂≤3

x₁-x₂≤4

x₁≥0; x₂≥0

Рис. 1.6.3. ОДЗ —пуста

2. одной точкой:

x₁+x₂ ≤l

x₁-x₂ ≤-1

x₁ ≥0; x₂ ≥0

Рис. 1.6.4. ОДЗ — одна точка