ДанныеСортировка…

Параметры сортировки задайте, как указано ниже на рисунке.

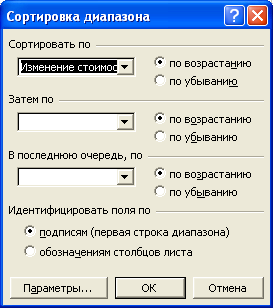
3. В ячейку B1 введите метку Ранг, а в ячейку B2 введите число 1. Выделите диапазон B2:B30 и выберите команду ПравкаЗаполнитьПрогрессия …В диалоговом окне установите опцию Шаг: равной 1 и щелкните на кнопке ОК.

4. Теперь определите значение медианы. Для этого сначала присвойте имя переменной n ячейке B30. В ячейке D1 задайте метку Ранг, а в ячейку D2 введите формулу =(n+1)/2. В ячейке D5 задайте метку Медиана. В ячейку D6 скопируйте из столбца процентного изменения стоимости акций значение, соответствующее вычисленному рангу медианы.

5. Постройте гистограмму процентных изменений стоимости акций для диапазона данных A1:A30, включая метку. Интервал входных значений задайте явно равным 2. Нижнюю границу диапазона входных значений примите равной –20, а верхнюю границу равной 0. Значения карманов вместе с меткой Карман расположите в ячейках F1:F12. Выведите гистограмму вместе с таблицей распределения частот в область H1:Р20. Можно ли считать, что распределение данных близко к нормальному?

6. В ячейке D9 задайте метку Среднее, а в ячейке D10 рассчитайте среднее значение процентного изменения. Уменьшите разрядность полученного значения до одного знака после запятой. Существенно ли отличаются друг от друга значения среднего и медианы?

Задание 6.

Определить медиану и среднее для служащих сферы общественного питания.

В таблице 4 содержатся данные о количестве служащих в 10 фирмах общественного питания.

Таблица 4. Количество служащих в фирмах общественного питания

Фирма	Количество служащих	Фирма	Количество служащих
1	471000	6	33000
2	183000	7	30000
3	133000	8	51700
4	90000	9	26170
5	44000	10	38000

1. В файле Описательная статистика.xls добавьте Лист4.

2. На Листе4 в ячейке A1 задайте метку Количество служащих, а в диапазон A2:A11 введите данные из Таблицы 4.

3. Постройте гистограмму для диапазона данных A1:A11, включая метку. Интервал входных значений задайте явно равным 20000. Нижнюю границу диапазона входных значений примите равной 26000, а верхнюю границу равной 486000. Значения карманов вместе с меткой Карман расположите в ячейках D1:D25. Расположите таблицу распределения частот в диапазоне F1:G26, а гистограмму – в диапазоне I1:M20. Какой характер распределения имеют данные?

4. В ячейку J25 введите метку Медиана. В ячейке J26 вычислите медиану, используя статистическую функцию МЕДИАНА.

5. В ячейку L25 введите метку Среднее. В ячейке L26 вычислите среднее, используя статистическую функцию СРЗНАЧ. Объясните причину отличия значений медианы и среднего.

Использование инструмента анализа Ранг и персентиль

Персентили – это характеристики набора данных, которые определяют ранги элементов в виде процентов таким образом, что наименьшему значению элемента данных соответствует персентиль, равный 0%, наибольшему – 100%, медиане – 50% и т.д. Промежуточные значения имеют персентили, расположенные с шагом 100/(n–1). Персентиль выражается в тех же единицах, что и набор данных. Например, 60-й персентиль эффективности продаж равен $385000 и характеризует деятельность определенного агента по продажам. Это означает, что приблизительно 60% других агентов имеют результаты ниже, чем у данного агента, а 40% агентов имеют более высокие результаты.

Персентили играют важную роль в качестве опорных характеристик данных. Чтобы обобщить основные черты распределения, достаточно знать пять базовых значений персентилей.

• Наименьшее значение данных (0-персентиль).

• Нижний квартиль (25-й персентиль, расположенный на расстоянии одной четверти от наименьшего значения).

• Медиана (50-персентиль).

• Верхний квартиль (75-й персентиль, расположенный на расстоянии одной четверти от наибольшего значения).

• Наибольшее значение данных (100-персентиль).

Нижний и верхний квартили определяют границы половины данных, расположенных в центре, а положение медианы относительно квартилей дает грубое представление о наличии или отсутствии ассиметрии. В инструменте Описательная статистика, как правило, опции К-ый наименьший задается ранг нижнего квартиля, а опции К-ый нибольший – ранг верхнего квартиля. Ранги квартилей определяются по следующим формулам:

Ранг нижнего квартиля = (1+Целое((n+1)/2))/2;

Ранг верхнего квартиля = (n+1) – Ранг нижнего квартиля,

где Целое означает функцию выделения целой части.

Задание 7.

Определить пять базовых показателей для набора данных о размерах выплат руководителям финансовых фирм.

В таблице 5 содержится список о размере выплат (заработная плата и премия) руководителям финансовых компаний (n=30).

Таблица 5. Выплаты руководителям финансовых компаний

Фирма	Зарплата и премия, дол.	Фирма	Зарплата и премия, дол.	Фирма	Зарплата и премия, дол.
1	1723000	11	1075000	21	1937000
2	1294000	12	1000000	22	3200000
3	1119000	13	901000	23	2063000
4	6910000	14	1936000	24	1726000
5	1960000	15	1458000	25	1393000
6	896000	16	3077000	26	1877000
7	746000	17	4840000	27	1674000
8	3273000	18	1190000	28	1537000
9	2101000	19	481000	29	743000
10	1384000	20	1040000	30	1242000

1. В файле Описательная статистика.xls добавьте Лист5.

2. На Листе5 в ячейке A1 задайте метку Выплаты, а в диапазон A2:A31 введите данные из Таблицы 5.

3. Выберите команду СервисАнализ данныхРанг и персентиль и задайте параметры как указано ниже на рисунке. Щелкните на кнопке ОК.

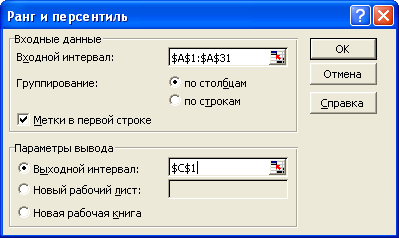
В полученной таблице выделите столбец со значениями персентилей (диапазон F2:F31) и уменьшите разрядность до одного знака после запятой.

4. Объедините диапазон ячеек H1:N1 и введите метку Базовые показатели.

5. В ячейку H2 введите метку Наименьшее значение, а в ячейку H3 скопируйте значение из ячейки D31.

6. В ячейку K2 введите метку Наибольшее значение, а в ячейку K3 скопируйте значение из ячейки D2.

7. В ячейке N2 задайте метку Медиана. В ячейке N3, используя функцию СРЗНАЧ, вычислите медиану как среднее двух значений с рангами 15 и 16 (ячейки D16:D17).

8. В ячейках H6 и L6 задайте метки Нижний квартиль и Верхний квартиль соответственно.

9. В ячейку H7 скопируйте значение из ячейки D24, что соответствует нижнему 24,1-персентилю (это число самое близкое к 25%) с рангом 23.

10. В ячейку L7 скопируйте значение из ячейки D9, что соответствует верхнему 75,8-персентилю (это число самое близкое к 75%) с рангом 8.

11. Чтобы сделать выводы о симметричности распределения, надо сравнить три значения: медиану и квартили. Проведем визуальное сравнение. Для этого постройте для соответствующих значений (выделив ячейки N3, H7, L7) точечную диаграмму, проставьте значения точек и удалите все надписи. Вид диаграммы показан на рисунке.

Как видим из диаграммы, значение медианы находится приблизительно посередине между квартилями, что соответствует симметричному распределению данных.