Частина друга

Розв’яжіть завдання 2.1. – 2.4. Запишіть відповідь у бланк відповідей.

1. Спростіть вираз .

2. Розв’яжіть нерівність .

3. Знайдіть похідну функції .

4. Основою прямого паралелепіпеда є ромб з периметром 20 см і діагоналлю 6 см. Більша діагональ паралелепіпеда дорівнює 10 см. Знайдіть об’єм паралелепіпеда.

Варіант 10

Частина друга

Розв’яжіть завдання 2.1. – 2.4. Запишіть відповідь у бланк відповідей.

1. Обчисліть інтеграл .

2. Знайдіть корені рівняння .

3. Тіло рухається прямолінійно за законом (м/с). У який момент часу швидкість тіла буде дорівнювати 8 м/с?

4. Діагональ осьового перерізу циліндра дорівнює 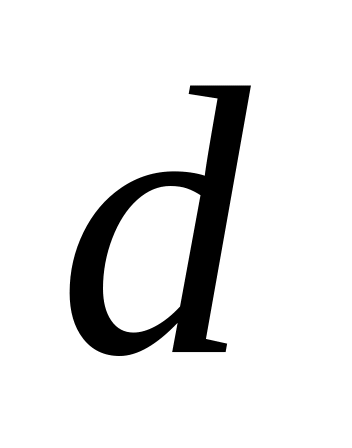і нахилена до площини основи під кутом . Знайдіть об’єм циліндра.

Варіант 11

Частина друга

Розв’яжіть завдання 2.1. – 2.4. Запишіть відповідь у бланк відповідей.

1. Розв’яжіть рівняння .

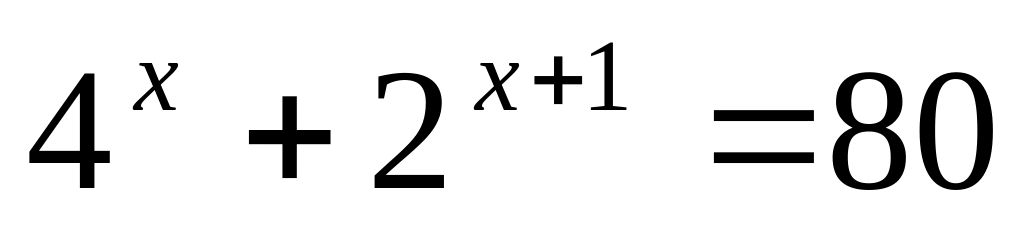2. У ящику лежать 12 білих кульок і кілька чорних. Скільки чорних кульок у ящику, якщо ймовірність витягнути навмання чорну кульку дорівнює .

3. Знайдіть проміжки спадання функції .

4. Катет прямокутного трикутника дорівнює a, а прилеглий кут - . Знайти площу бічної поверхні конуса, утвореного обертанням цього трикутника навколо катета.

Варіант 12

Частина друга

Розв’яжіть завдання 2.1. – 2.4. Запишіть відповідь у бланк відповідей.

1. Спростіть вираз .

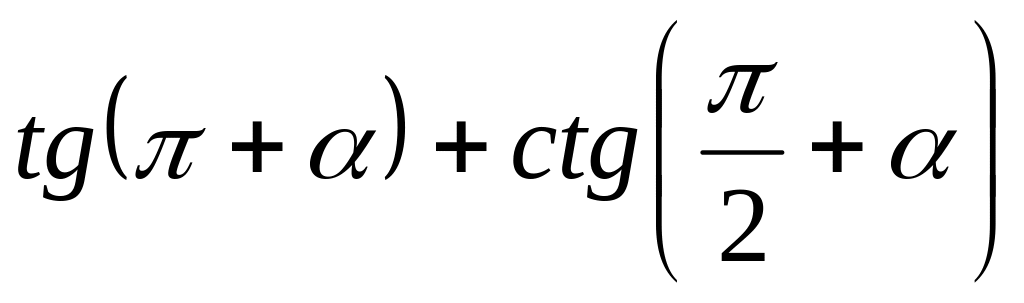2. Розв’яжіть рівняння .

3. Обчисліть інтеграл .

4. У кулі, об’єм якої 36π см³, проведено переріз. Радіус кулі, один з кінців якого належить перерізу, утворює з площиною перерізу кут 45º. Знайдіть площу перерізу.

Варіант 13

Частина друга

Розв’яжіть завдання 2.1. – 2.4. Запишіть відповідь у бланк відповідей.

1. Відомо, що ; . Виразіть через а і b .

2. Розв’яжіть нерівність .

3. Знайдіть корені рівняння .

4. З точки до площини проведено дві похилі, проекції яких на площину дорівнюють 9 см і 16 см. Знайдіть відстань від даної точки до площини, якщо одна з похилих на 5 см довша за другу.

Варіант 14

Частина друга

Розв’яжіть завдання 2.1. – 2.4. Запишіть відповідь у бланк відповідей.

1. Спростіть вираз .

2. Розв’яжіть рівняння: .

3. Обчисліть інтеграл .

4. У трикутнику АВС , , АВ=3. Знайдіть об’єм тіла, утвореного обертанням даного трикутника навколо прямої ВС.

Варіант 15

Частина друга

Розв’яжіть завдання 2.1. – 2.4. Запишіть відповідь у бланк відповідей.

1. Розв’яжіть рівняння: .

2. Розв’яжіть нерівність .

3. На графіку функції 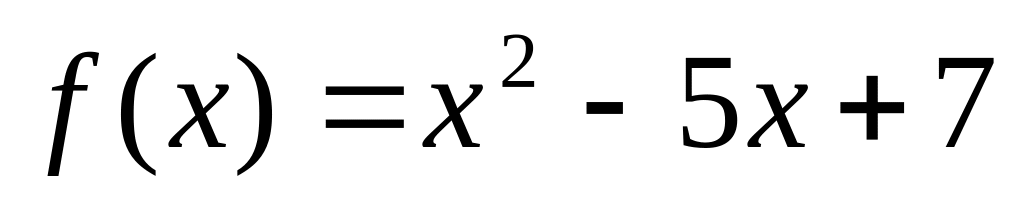знайдіть точку, в якій дотична утворює кут 45° із додатним напрямом осі абсцис.

4. Хорду, що лежить в основі конуса, з його вершини видно під кутом 60°, а з центра основи – під прямим кутом. Знайдіть площу бічної поверхні конуса, якщо його твірна дорівнює 4 см.

Варіант 16

Частина друга

Розв’яжіть завдання 2.1. – 2.4. Запишіть відповідь у бланк відповідей.

1. Розв’яжіть рівняння .

2. Знайдіть значення похідної функції у точці .

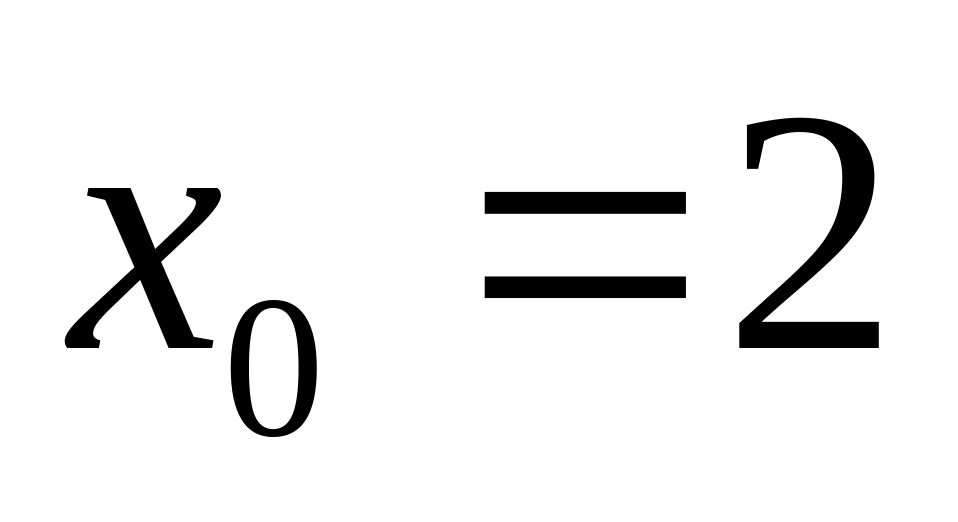3. Розв’яжіть рівняння .

4. Знайдіть об’єм правильної чотирикутної піраміди, сторона основи якої дорівнює 6 см, а діагональний переріз є рівностороннім трикутником.

Варіант 17

Частина друга

Розв’яжіть завдання 2.1. – 2.4. Запишіть відповідь у бланк відповідей.

1. Знайдіть , якщо і .

2. Розв’яжіть рівняння .

3. Обчисліть інтеграл .

4. Знайдіть площу повної поверхні прямокутного паралелепіпеда, якщо його діагональ більша за лінійні виміри відповідно на 1 см, 9 см і 10 см.

Варіант 18

Частина друга

Розв’яжіть завдання 2.1. – 2.4. Запишіть відповідь у бланк відповідей.

1. Знайдіть значення , якщо .

2. Розв’яжіть рівняння .

3. Швидкість руху точки задається рівнянням (м/с). Знайдіть рівняння руху , якщо м.

4. Радіус основи конуса дорівнює , а його осьовий переріз – прямокутний трикутник. Знайдіть об’єм конуса.

Варіант 19

Частина друга

Розв’яжіть завдання 2.1. – 2.4. Запишіть відповідь у бланк відповідей.

1. Спростіть вираз .

2. Розв’яжіть нерівність .

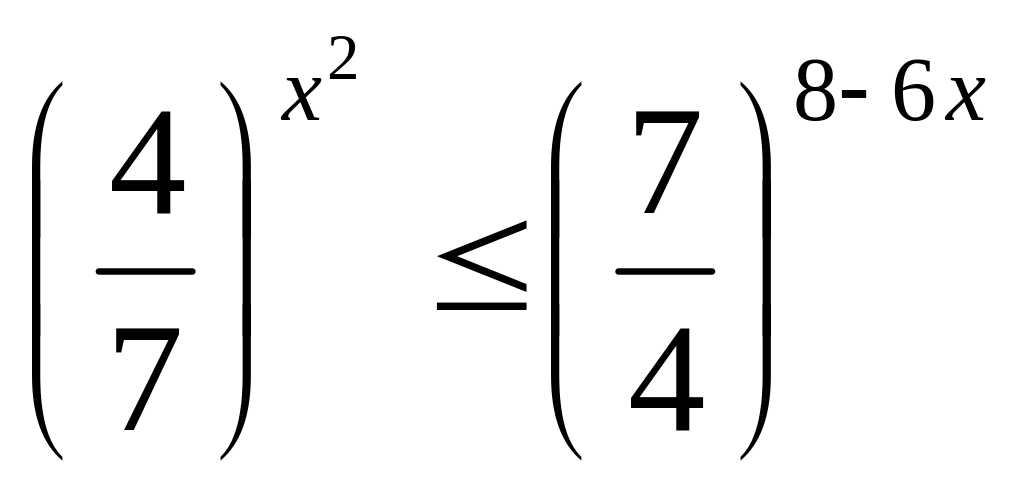3. Укажіть область визначення функції .

4. У нижній основі циліндра проведено хорду завдовжки 8 см, яка знаходиться на відстані 3 см від центра цієї основи. Знайдіть площу осьового перерізу циліндра, якщо його висота дорівнює 6 см.

Варіант 20