Тема 1.15. Работа и мощность. Кпд.

1.15.1. Работа силы на прямолинейном участке пути.

1.15.2. Работа переменной силы на криволинейном пути. Графическое изображение работы.

1.15.3. Теорема о работе равнодействующей .

1.15.4. Мощность. Коэффициент полезного действия.

1.15.5. Работа и мощность силы, приложенной к твёрдому телу, вращающемуся вокруг неподвижной оси.

1 .15.1. Пусть точка М тела, к которой приложена постоянная по модулю и по направлению сила , перемещается прямолинейно из положения М в положение М' (рис. 1.15.1.), причем угол между направлением силы и направлением перемещения точки равен , а путь, проходимый точкой, равен S.

Силу можно разложить на две составляющие: нормальную не совершающую работы, и касательную , модуль которой .

Так как работу совершает только вторая составляю­щая, то работа силы будет равна

. (1.15.1.)

Работа постоянной силы при прямолинейном перемеще­нии ее точки приложения равна произведению модуля силы на длину пути, пройденного ее точкой приложения, и на косинус уела между направлением силы и направлением движения ее точки приложения.

Работа силы есть скалярная величина, т. е. вполне определяется ее численным значением и знаком.

Из формулы (1.15.1.) видно, что

1. если , то (силы, направление которых составляет острый угол с направлением дви­жения их точки приложения, совершают положительную работу);

2. если , то (силы, направление которых составляет тупой угол с направлением движения их точки приложения, совершают отрицательную работу);

3. если или , то .

За единицу работы в Международной системе единиц (СИ) принимается работа силы в 1 Н при перемещении ею тела на расстояние в 1 м в направлении действия силы. Эта единица называется джоулем (сокращенно—Дж).

Установленное в механике понятие работы (называемой иногда механической работой) возникло из повседневного опыта. Однако нужно заметить, что оно не всегда совпа­дает с тем, что понимают под работой с физиологической точки зрения. Так, человек, неподвижно держащий тяже­лый груз на вытянутых руках, не совершает, очевидно, никакой механической работы (S=0), в физиологической же точки зрения он совершает, конечно, определенную (при большом весе груза и весьма значительную) работу.

1.15.2. Пользуясь установленным в предыдущем пункте по­нятием работы постоянной силы на прямолинейном пути, перейдем к вычислению работы си­лы в самом общем случае.

П усть точка приложения М переменной по модулю и по нап­равлению силы перемещается из положения А в положение В, опи­сывая при этом некоторую криво­линейную траекторию (рис. 1.15.2.). Разобьем путь , пройден­ный точкой, на очень большое чис­ло n столь малых участков, что без большой погрешности можно счи­тать каждый такой участок пря­молинейным, а силу, действующую на данном участке,— постоянной и по модулю, и по направлению. Обозначим через постоянные для данных участков пути значения модуля переменной силы , через - длины соответствующих (прямоли­нейных) участков пути и через —углы между соответствующими направлениями силы и ско­рости точки ее приложения.

Полная работа А переменной силы на конечном пути АВ будет, очевидно, равна сумме работ на всех его отдель­ных участках:

.

Ясно, что чем на большее число участков n мы разобьем путь, пройденный точкой приложения переменной силы , тем точнее вычисляется работа этой силы на данном пути. В пределе, когда число участков n станет бесконечно большим, длина каждого из них станет бесконечно малой величиной.

Работа силы на бесконечно малом перемещении ее точки приложения называется элементарной работой. Обозначая элементарную работу силы через и длину бесконечно малого элемента пути через dS, будем иметь

. (1.15.2.)

Тогда работа на всём конечном пути

. (1.15.3.)

Работа переменной силы на конечном пути равна интегралу от элементарной работы данной силы, вычислен­ному в пределах изменения пути точки приложения силы.

С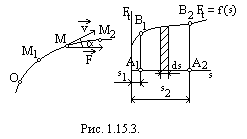 ейчас же, заметив, что вычисление данного интеграла во многих случаях представляет значительные трудности, перейдем к более простому и часто применяемому в тех­нике графическому способу вычисления работы перемен­ной силы.

Пусть точка М приложения переменной по модулю и по направлению силы перемещается из положения в положение , которые определяются на ее траектории соответствующими расстояниями и отсчитываемыми от некоторого начала О (рис. 1.15.3.).

Возьмем прямоугольную систему координат (рис. 1.15.3.) и в выбранных масштабах будем откладывать: по оси абсцисс расстояние s точки от начала отсчета, а по оси ординат—соответствующую величину проекции силы на направление скорости точки М ее приложения, т. е. алгеб­раическое значение касательной составляющей данной силы .

Соединяя точки с данными координатами s и F_t непре­рывной кривой, получим график зависимости .

Работа силы на ее пути S будет изображаться в соответствующем масштабе площадью фигуры (рис. 1.15.3.), ограниченной осью абсцисс, кривой и двумя ординатами, соответствующими начальному и ко­нечному положению точки приложения силы .

При вычислении работы силы графическим способом нужно, конечно, учитывать масштабы, в которых откла­дывались на графике расстояния s и соответ­ствующие им значения модуля силы F_t.

1.15.3. Теорема. Работа равнодействующей нескольких сил на некотором пути равна алгебраической сумме работ составляющих сил на том же пути:

,

где = - равнодействующая сил .

1.15.4. Мощностью силы называется величина, характеризующая быстроту, с которой этой силой совершается работа в данный момент времени.

Средняя мощность силы за некоторый промежуток времени t равна отношению совершённой ею за это время работы А к данному промежутку времени:

.

Мощность Р силы в данный момент времени t равна отношению элементарной работы dА силы за бесконечно малый промежуток времени, начинающийся в момент t, к величине dt этого промежутка времени:

. (1.15.4.)

В СИ за единицу мощности принимается мощность, при которой работа в 1 джоуль совершается в 1 секунду. Эта единица мощности называется ваттом (сокра­щенно—Вт)

1 Вт=1 Дж/с.

Формуле (1.15.4.) мощности в данный момент можно при­дать другой вид, если подставить в нее установленное ранее [формула (1.15.2.)] выражение элементарной работы:

Мощность силы в данный момент равна произведению соот­ветствующих этому моменту времени модуля данной силы, модуля скорости точки ее приложения и косинуса угла между направлениями силы и скорости точки ее прило-окения.

При работе любой машины часть потребляемой ею мощ­ности тратится не на совершение полезной работы, а на преодоление так называемых вредных сопротивлений, не­избежно возникающих при работе машины. Так, например, мощность, потребляемая токарным станком, тратится не только на совершение полезной работы—снятие стружки, но и на преодоление трения в движущихся частях машин и сопротивления их движению со стороны воздуха.

Отношение полезной мощности Р_П машины к потреб­ляемой ею мощности Р или отношение полезной работы за некоторый определенный промежуток времени ко всей затраченной работе А за тот же промежуток вре­мени называется механическим коэффициентом полезного действия.

Обозначая, как это обычно принято, коэффициент по­лезного действия (сокращенно КПД) греческой буквой (эта), будем иметь

. (1.15.5.)

КПД является одной из важнейших характеристик машины, показывающей, насколько рационально исполь­зуется потребляемая ею мощность.

Полностью вредные сопротивления никогда не могут быть устранены, и потому КПД всегда меньше единицы.

1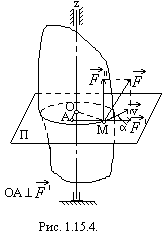 .15.5. Пусть в некоторой точке М твердого тела, вращающе­гося вокруг неподвижной оси z (рис. 1.15.4.), приложена сила . Разложим эту силу на две взаимно перпендику­лярные составляющие: , лежащую в плоскости П, пер­пендикулярной к оси z вращения тела, и , перпенди­кулярную к этой плоскости, т. е. параллельную оси z.

Тогда элементарная работа dА силы равна элементарной работе составляющей

,

где .

Так как , то .

Работа силы при повороте тела на конечный угол будет равна

.

В случае, когда , будем иметь

.

Работа А при постоянном вращающем моменте равна произведению этого момента на угол поворота тела.

Найдём теперь мощность силы, приложенной к вращающемуся телу:

.

Мощность Р силы, приложенной к вращающемуся телу, равна произведению вращающего момента этой силы на угловую скорость тела.