Тема 1.2. Плоская система сходящихся сил.

1.2.1. Система сходящихся сил.

1.2.2. Геометрические способы сложения сходящихся сил.

1.2.3. Аналитический метод сложения сходящихся сил.

1.2.4. Условия равновесия плоской системы сходящихся сил.

1.2.5. Разложение силы на две сходящиеся составляющие.

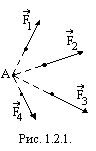
1.2.1. Система сил, линии действия которых лежат в одной плоскости и пересекаются в одной точке (рис. 1.2.1.), называется плоской системой сходящихся сил. Используя следствие 1 из аксиом статики , любую систему сходящихся сил можно заменить эквивалентной системой сил, приложенных к одной точке (рис. 1.2.2.).

1.2.2. Наиболее просто решается задача о сложении двух сил, приложенных в одной точке. Для этого надо воспользоваться третьей аксиомой статики (рис. 1.2.3.).

; ;

(1.2.1)

.

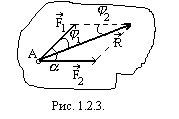
П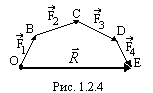 ри сложении нескольких сил (рис. 1.2.1.) можно воспользоваться правилом многоугольника (рис. 1.2.4.): от произвольной точки откладываем вектор, равный силе ; от конца откладываем вектор, равный силе ; от конца откладываем вектор, равный силе и т.д. Затем, соединяя начало вектора (точка О) с концом последнего (точка Е), получаем главный вектор данной системы сил. Построенная фигура называется силовым многоугольником. Для сходящейся системы сил понятие главного вектора эквивалентно понятию равнодействующей силы.

Таким образом, равнодействующая плоской системы сходящихся сил равна их геометрической сумме: .

1.2.3. Аналитическое определение равнодействующей системы сходящихся сил, т.е. определение модуля и направления искомого вектора путём вычисления, основано на применении метода проекции.

Проекция равнодействующей системы сходящихся сил на какую-либо ось равна алгебраической сумме проекций составляющих сил на эту ось:

(1.2.2.)

г де - проекции, соответственно, сил на ось Ox; - проекции, соответственно, сил на ось Oy (рис. 1.2.5.).

Модуль равнодействующей плоской системы сходящихся сил определяется формулой

(1.2.3.)

Углы между равнодействующей и координатными осями, а следовательно, и направление равнодействующей определяется формулами

(1.2.4.)

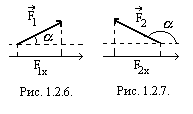Примечание. Проекцией точки на ось называется основание перпендикуляра, опущенного из данной точки на данную ось. Длина отрезка оси ( ), заключённого между проекциями на ось начала и конца данного вектора ( ), взятого с определённым знаком, называется проекцией этого вектора на данную ось (рис. 1.2.6.). Проекция вектора на ось считается положительной, если вектор составляет острый угол с положительным направлением оси (рис. 1.2.6.), и отрицательной, когда вектор составляет с направлением оси проекции тупой угол (рис. 1.2.7.).

Проекция вектора на ось равна модулю этого вектора, умноженному на косинус угла между вектором и положительным направлением оси проекции (рис. 1.2.6.):

(1.2.5.)

Проекция вектора на ось представляет собой не векторную, а скалярную алгебраическую величину.

1.2.4. Из выше сказанного следует, что всякая система сходящихся сил может быть заменена равнодействующей. Ясно, что если такая система сходящихся сил находится в равновесии, то равнодействующая должна равняться нулю.

Равенство нулю равнодействующей – необходимое и достаточное условие равновесия системы сходящихся сил.

Соответственно двум способам определения равнодействующей условие равновесия плоской системы сходящихся сил может быть выражено в двух формах.

1) Условие равновесия в геометрической форме. Геометрически равнодействующая сходящихся сил определяется как замыкающая сторона силового многоугольника, построенного на этих силах. Если равнодействующая равна нулю, то нужно, чтобы равнялась нулю и замыкающая сторона и, следовательно, силовой многоугольник замыкался сам по себе. С другой стороны, замыкание силового многоугольника означает, что равнодействующая сходящихся сил равна нулю. Отсюда получается следующее условие: для равновесия системы сходящихся сил необходимо и достаточно, чтобы силовой многоугольник, построенный для этой системы сил, был замкнут.

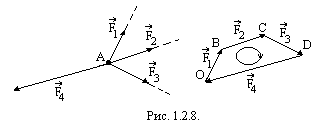На рис. 1.2.8. построен замкнутый силовой многоугольник для находящейся в равновесии плоской системы сил . Необходимо заметить, что в замкнутом силовом многоугольнике конец вектора последней силы совпадает с началом вектора первой, а стрелки векторов всех сил указывают одну и ту же сторону обхода периметра многоугольника.

2) Условие равновесия в аналитической форме. Условием равновесия системы сходящихся сил является равенство нулю модуля равнодействующей ( ), т. е. проекции ( ) равнодействующей силы на оси координат (на каждую из двух любых взаимно перпендикулярных осей) должны быть равны нулю. Отсюда для плоской системы сходящихся сил получим два уравнения равновесия этих сил:

и . (1.2.6.)

Таким образом, для равновесия плоской системы сходящихся сил необходимо и достаточно, чтобы порознь равнялись нулю суммы проекций всех сил на каждую из двух любых взаимно перпендикулярных осей, лежащих в плоскости действия сил.

1.2.5. Разложить силу на составляющие – это значит найти такую систему двух или нескольких сил, которая бы производила на тело то же самое действие, что и одна данная сила. Другими словами, разложить силу, например, на две составляющие – это значит найти такие две силы, равнодействующая которых была бы равна данной силе. Решений у такой задачи может быть сколько угодно много. Чтобы решение было определённым, необходимо задать дополнительные условия, например: 1) задание двух направлений, по которым должны действовать составляющие; 2) задание модуля и направления одной из составляющих сил; 3) задание модуля обеих составляющих; 4) задание модуля одной составляющей силы и направления другой.

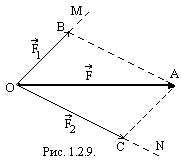Рассмотрим первый, наиболее часто встречающиеся, случай. Данную силу требуется разложить на две сходящиеся составляющие силы, направления которых ОМ и ON заданы (рис. 1.2.9.)

Для решения задачи из конца А вектора силы проводим прямые АВ и АС, соответственно параллельно прямым ОN и ОМ. Получается параллелограмм OABC, для которого сила является диагональю. Векторы и дают в том же масштабе, что и заданная сила , искомые составляющие и .