Тема 1.9. Простейшие виды движения твёрдого тела.

1. Поступательное движение твёрдого тела.

2. Вращательное движение твёрдого тела относительно неподвижной оси.

3. Траектории, скорости и ускорения точек вращающегося твёрдого тела.

4. Передачи вращательного движения.

1.9.1. Поступательным движением твердого тела называется такое движение, при котором всякая прямая, неизменно связанная с этим телом, движется, оставаясь параллель­ной своему натлыному положению.

Примерами поступательного движения тела могут слу­жить: движение кузова автомашины, движущейся по пря­молинейному пути, движение поршня двигателя и т. д. Неправильно, однако, ду­мать, что при поступа –тельном движении тела траектории его точек должны быть непре­менно прямыми линиями. Так, например, спарник АВ (рис. 1.9.1.), соединяющий кривошипы и двух соседних колее паровоза, совершает поступательное дви­жение, хотя его точки и будут двигаться по окружностям. В самом деле, при вращении кривошипов и во­круг их осей и положение спарника АВ будет изме­няться. Но при равенстве длин кривошипов и при длине спарника, равной расстоянию между осями , четырех­угольник будет всегда оставаться параллелограм­мом, следовательно, спарник АВ будет всегда параллельным основанию , т. е. движется, оставаясь параллельным своему начальному положению. В то же время точки А и В спарника, а следовательно, и все остальные его точки движутся по окружностям, радиус которых равен длине кривошипа.

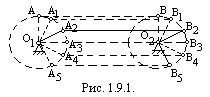
Траекториями точек тела при его поступательном дви­жении могут быть какие угодно кривые: прямолинейное движение тела есть только частный случай поступатель­ного движения.

Заметим также, что термин «поступательное движение» применим только к движению тела, но не к движению одной точки. Понятие «движется, оставаясь параллельной своему начальному положению» никак не применимо к точке, не имеющей размеров.

Теорема. При поступательном движении твердого тела все его точки движутся по одинаковым (при наложении совпадающим) траекториям и имеют в каждый данный момент равные скорости и равные ускорения.

Из теоремы следует, что поступательное движение тела вполне определяется движением какой-либо одной его точки. Таким образом, задача изучения поступательного движения твёрдого тела сводится к уже рассмотренным ранее задачам кинематики точки.

Скорость и ускорение, общие для всех точек поступательно движущегося тела, называются скоростью и ускорением этого тела.

Заметим, что говорить о скорости и ускорении тела можно только в случае его поступательного движения. Во всех остальных случаях различные точки тела имеют различные скорости и различные ускорения.

1 .9.2. Вращательным движением называется такое движение твердого тела, при котором все его точки, лежащие на некоторой прямой, называемой осью вращения, остаются неподвижными. ( Вращающееся тело может и не иметь своих точек на геомет­рической оси вращения, т. е. не иметь само неподвижных точек. Например, колесо, надетое на материальную ось, или человек, сидя­щий на карусели. Но если точки, расположенные на геометрической оси вращения, неизменно присоединить к вращающемуся телу, то они будут оставаться неподвижными при вращении тела.)

Для того чтобы осуществить вращательное движение тела, достаточно закрепить неподвижно две какие-нибудь его точки (например, при помощи под­шипника А и подпятника В, рис. 1.9.2.), тогда прямая, проходящая через эти две точки, будет осью вращения тела. При вращательном движении тела различные его точки движутся, вообще говоря, по-разному. Однако и для вра­щательного движения можно отыскать такие кинематические характеристики, которые были бы общими для всех точек тела.

Пусть какое-нибудь твердое тело (изображенное для простоты на рис. 1.9.2. в виде цилиндра) вращается вокруг неподвижной оси г. Проведем через ось вращения z неподвижную полуплос­кость 1 и полуплоскость 11, неизменно связанную с вра­щающимся телом.

Угол между двумя полуплоскостями, проходящими через ось вращения тела, неподвижную и неизменно связанную с вращающимся телом, называется углом поворота тела.

Установим на оси вращения z положительное направ­ление и условимся считать угол поворота тела положи­тельным, когда он отсчитывается от неподвижной плос­кости 1 в сторону, противоположную вращению часовой стрелки, если смотреть на него с положительного конца оси вращения. Заданием величины и знака угла поворота вполне определяется положение полуплоскости 11 и неизменно связанного с ней вращающегося тела.

При вращении тела вокруг оси г угол поворота тела изменяется с течением времени, следовательно, он явля­ется некоторой функцией времени:

. (1.9.1.)

Уравнение (1.9.1.), устанавливающее зависимость между углом поворота тела и временем его движения, назы­вается уравнением вращательного движения тела. Этим уравнением вполне определяется вращательное движение тела, так как для каждого момента времени t можно найти соответствующее ему значение угла пово­рота тела и тем самым определить положение тела в этот момент.

Угол поворота в механике обычно измеряют в радианах. Иногда в практичес­ких задачах угол поворота выражают числом оборотов тела. Принимая во внимание, что один оборот тела, т. е. его поворот на 360°, соответствует радиан, мы получаем зависимость между углом поворота тела в радианах и числом его оборотов:

.

Пусть за некоторый промежуток времени угол получил приращение . Величина называется средней угловой скоростью тела за данный промежуток времени. Предел, к которому стремится средняя угловая скорость при стремящимся к нулю, называется угловой скоростью тела в данный момент времени ,

. (1.9.2.)

Значение угловой скорости тела для данного момента времени может быть положительным или отрицательным в зависимости от того, в какую сторону вращается тело. Когда тело вращается против часовой стрелки, если смот­реть с положительного конца оси вращения, то и угловая скорость положительна. Если тело вращается по часовой стрелке, то угловая скорость отри­цательна. Следовательно, знак угловой скорости указыва­ет, в какую сторону в данный момент вращается тело.

Исходя из определения угловой скорости, можно найти и ее размерность:

.

Так как угол в механике измеряется в радианах, а время — в секундах, то угловая скорость измеряется в радианах в секунду ( ).

На практике часто угловую скорость тела выражают не в радианах в секунду, а так называемой частотой вращения, выраженной числом оборотов в минуту, обо­значая ее буквой . Нетрудно найти зависимость между и .

Так как один оборот тела соответствует его повороту на угол в радиан, то

Таким образом, получаем важную для практики зави­симость между угловой скоростью тела в радианах в секунду и его угловой скоростью п в оборотах в минуту:

(1.9.3.)

Нужно помнить, что в этой формуле всегда выра­жается в рад/с, а п — в об/мин.

Если тело вращается неравномерно, т. е. если прира­щения угла поворота тела за равные промежутки вре­мени не равны, то его угловая скорость изменяется с течением времени и будет являться, следовательно, также некоторой функцией времени:

.

Величина, характеризующая быстроту изменения угло­вой скорости тела, называется его угловым ускорением.

Пусть за некоторый промежуток времени угловая скорость получила приращение . Величина называется средним угловым ускорением тела за данный промежуток времени . Предел, к которому стремится среднее угловое ускорение при стремящемся к нулю, называется угловым ускорением тела в данный момент времени ,

. (1.9.4.)

Учитывая формулу (1.9.2.), получим для углового ускорения:

. (1.9.5.)

Единица углового ускорения в Международной системе единиц (СИ) – радиан в секунду в квадрате ( ).

Если , то , если , то . В том случае, когда знаки угловой скорости и углового ускорения совпадают, вращательное движение называется ускоренным, когда противоположны – замедленным.

1.9.3. При вращении тела вокруг неподвижной оси все его точки описывают окружности, лежащие в плоскостях, перпендикулярных к оси вращения z. Центры этих окружностей лежат на оси вращения и, следовательно, радиус каждой из них равен расстоянию соответствующей точки тела от оси вращения.

О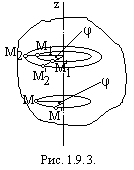 чевидно, что радиусы всех данных окружностей по­ворачиваются за один и тот же промежуток времени на один и тот же угол , равный приращению угла поворота тела за этот промежуток времени, однако точки, лежащие на разных расстояниях от оси вращения (точки и на рис. 1.9.3.), опишут при этом дуги различной длины.

Зная угловую скорость тела и расстояние какой-нибудь точки М тела от оси вращения, можно найти и скорость этой точки (Скорость точки вращающегося тела, характеризующую своим модулем быстроту ее движения по дуге траектории (измеряемой в линейных единицах), иногда называют линейной скоростью в отличие от угловой скорости тела, характеризующей быстроту изменения угла его поворота.):

Численное значение скорости точки вращающегося тела равно произведению угловой скорости тела на расстояние данной точки от оси вращения:

(1.9.6.)

Направлен вектор скорости точки по касательной к траектории точки, следовательно, перпендикулярно к ее радиусу вращения, в сторону движения точки. Из фор­мулы (1.9.6.) следует, что скорости точек вращающегося тела пропорциональны расстояниям этих точек от оси вращения.

Учитывая формулу (1.9.3.) ,получим для линейной скорости:

, (1.9.7.)

где d—диаметр вращающегося цилиндрического тела, п— число оборотов тела в минуту.

При любом вращательном движении тела скорость v его точек непременно изменяется (только по направлению при равномерном вращательном движении или по направ­лению и по модулю при неравномерном вращательном движении), следовательно, точки вращающегося тела всегда движутся с некоторым ускорением.

Ускорение точки вращающегося тела, как и ускорение всякого криволинейного движения, может быть разложено на касательное ускорение и нормальное ускорение :

, (1.9.8.)

(1.9.9.)

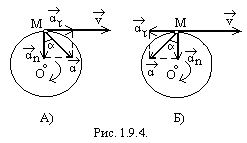
Направление вектора касательного ускорения точки совпадает с направлением вектора ее скорости при ускоренном вращении тела (рис. 1.9.4., А) и противоположно скорости в случае замедленного вращения (рис. 1.9.3., Б). Вектор же нормального ускоре­ния точки всегда направлен по ра­диусу окружности, описываемой точ­кой, к центру этой окружности (рис. 1.9.4.).

Зная касательное и нормальное ускорения точки, всегда можно (при необходимости) найти модуль и на­правление ускорения , являющего­ся диагональю прямоугольника, по­строенного на векторах и (рис. 1.9.4.):

. (1.9.10.)

1.9.4. Передача вращательного движения от одной машины к другой или внутри машины от одного ее вала к другому осуществляется разнообразными механизмами, носящими название передач.

Передачи могут быть разделены на передачи гибкой связью (ременную, канатную, цепную) и передачи, осу­ществляемые путем непосредственного соприкосновения (фрикционную, зубчатую и др.).

Валы и закрепленные на них шкивы и колеса называются ведущими, когда они передают движение, и ведомыми, когда они его воспринимают.

Отношение угловых скоростей двух валов (шкивов или колес) называется передаточным отношением.

Так как угловая скорость тела в рад/с пропорцио­нальна (формула (1.9.3.) ) его угловой скорости n в об/мин, то, обозначая передаточное отношение буквой и с соответ­ствующим двойным индексом, будем иметь

или .

1. Передаточное отношение ременной передачи равно об­ратному отношению радиусов (или диаметров) шкивов.

.

2. Передаточное отношение цилин­дрической фрикционной передачи равно обратному отноше­нию радиусов (или диаметров) колес:

.

3. Передаточное отношение двух находящихся в зацепле­нии зубчатых колес равно обратному отношению их чисел зубьев.

Многоступенчатой передачей называется механизм, состоящий из ряда соеди­ненных между собой простых передач.

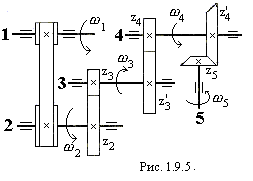
На рис. 1.9.5. изображена в качестве примера схема многоступенчатой передачи от вала 1 к валу 5, состоящей из ременной передачи, двух пар цилиндрических зубчатых колес и одной пары конических зубчатых колес.

Шкивы и колёса жёстко закреплены на соответствующих валах (это обозначено на схеме крестиками). Диаметры шкивов и . Числа зубьев колёс обозначены буквой z с соответствующими индексами.

Передаточное отношение данной передачи .

Передаточные отношения простых передач, входящих в состав данной многоступенчатой передачи,

, , , .

Перемножив почленно передаточные отношения, найдём

.

Таким образом, передаточное отношение многоступенчатой передачи равно произведению передаточных отношений всех входящих в её состав простых передач:

.

Передаточное отношение многоступенчатой передачи можно вычислить, зная, как определяются передаточные отношения простых передач, входящих в её состав.

Для двухступенчатой передачи цилиндрическими зуб­чатыми колесами от вала 2 к валу 4, изображенной на рис. 1.9.5, передаточное отношение

.

Для всей многоступенчатой передачи от вала 1 к ва­лу 5 абсолютное значение передаточного отношения

.

П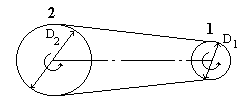 ример 1. Шкив 2 приводит­ся в движение из состояния покоя бесконечным ремнем от шкива 1 дви­гателя. Диаметры шкивов: , ; угловое ускорение шкива 1 в период пуска двигателя постоянно и равно рад/с². Определить частоту вра­щения шкива 2 через 15 с после начала движения.

Решение. Так как угловое ускорение постоянно, то угловая скорость шкива 1 через 15 с после пуска двигателя рад/с.

Передаточное отношение между шкивами

.

Отсюда угловая скорость шкива 2 через 15 секунд

рад/с

и тогда его частота

об/мин.

Данную задачу можно было бы решить и иначе. Отношение угловых ускорений двух валов также равно передаточному отношению между ними: . Пользуясь этим, можно было бы, не определяя угловой скорости шкива 1, определить по передаточному отношению угловое ускорение шкива 2, а затем его угловую скорость по формуле .