
- •Технической механике теоретическая механика
- •Пояснительная записка.
- •Тема 1.1. Основные понятия и аксиомы статики.
- •Вопросы для самопроверки.
- •Для заметок.
- •Тема 1.2. Плоская система сходящихся сил.
- •Вопросы для самопроверки.
- •Задачи.
- •Тема 1.3. Момент силы относительно точки. Пара сил.
- •Вопросы для самопроверки.
- •Задачи.
- •Для заметок.
- •Тема 1.4. Плоская система произвольно расположенных сил.
- •Вопросы для самопроверки.
- •Задачи.
- •Для заметок.
- •Тема 1. 5. Произвольная пространственная система сил.
- •Вопросы для самопроверки.
- •Задачи.
- •Для заметок
- •Тема 1.6. Центр тяжести тела.
- •Вопросы для самопроверки.
- •Задачи.
- •Для заметок.
- •Тема 1.7. Основные понятия кинематики.
- •Тангенсальная составляющая ускорения
- •Вопросы для самопроверки.
- •Задачи.
- •Тема 1.8. Частные случаи движения точки.
- •Задачи.
- •Для заметок
- •Тема 1.9. Простейшие виды движения твёрдого тела.
- •Вопросы для самопроверки.
- •Задачи.
- •Для заметок.
- •Тема 1.10. Сложное движение точки.
- •Вопросы для самопроверки.
- •Задачи.
- •Для заметок.
- •Тема 1.11. Сложное движение твёрдого тела.
- •Вопросы для самопроверки.
- •Задачи.
- •Для заметок.
- •Тема 1.12. Основные понятия и законы динамики.
- •Вопросы для самопроверки.
- •Задачи.
- •Тема 1.13. Основы кинетостатики.
- •Вопросы для самопроверки.
- •Задачи.
- •Для заметок.
- •Тема 1.14. Трение.
- •Вопросы для самопроверки.
- •Задачи.
- •Для заметок.
- •Тема 1.15. Работа и мощность. Кпд.
- •Вопросы для самопроверки.
- •Задачи.
- •Для заметок.
- •Тема 1.16. Общие теоремы динамики.
- •Вопросы для самопроверки.
- •Задачи.
- •Для заметок.
- •Вопросы для подготовки к зачёту по теоретичесой механике.
- •Список литературы.
Тангенсальная составляющая ускорения
![]() (1.7.5.)
(1.7.5.)
т.е. равна первой производной по времени от модуля скорости, определяя тем самым быстроту изменения скорости по модулю.
Найдём вторую составляющую
ускорения. Можно доказать, что при
![]() векторы
и
оказываются взаимно перпендикулярными.
Так как вектор скорости
направлен по касательной к траектории,
то вектор
,
перпендикулярный вектору скорости,
направлен к центру её кривизны. Вторая
составляющая ускорения, равная
векторы
и
оказываются взаимно перпендикулярными.
Так как вектор скорости
направлен по касательной к траектории,
то вектор
,
перпендикулярный вектору скорости,
направлен к центру её кривизны. Вторая
составляющая ускорения, равная
![]() ,
(1.7.6.)
,
(1.7.6.)
называется нормальной составляющей ускорения и направлена по нормали к траектории к центру её кривизны (поэтому её называют также центростремительным ускорением).
П олное
ускорение тела есть
геометрическая сумма тангенсальной и
нормальной составляющих (рис. 1.7.6.):
олное
ускорение тела есть
геометрическая сумма тангенсальной и
нормальной составляющих (рис. 1.7.6.):
![]() .
(1.7.7.)
.
(1.7.7.)
В зависимости от тангенсальной и нормальной составляющих ускорения движение можно классифицировать следующим образом:
 ,
,
 - прямолинейное равномерное движение;
- прямолинейное равномерное движение;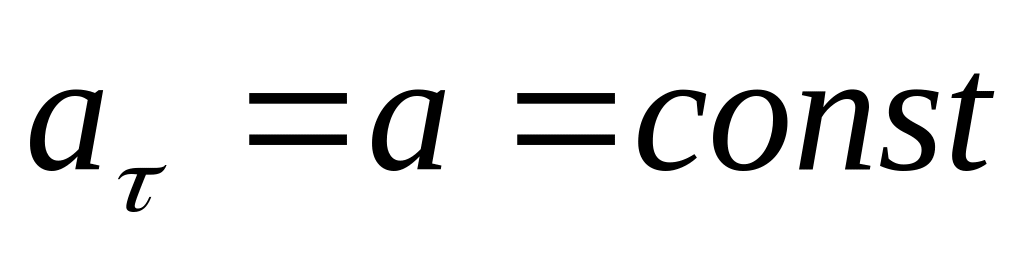 ,
-
прямолинейное равнопеременное движение;
,
-
прямолинейное равнопеременное движение; ,
-
прямолинейное движение с переменным
ускорением;
,
-
прямолинейное движение с переменным
ускорением;,
 - равномерное движение по окружности;
- равномерное движение по окружности;,
 -
равномерное криволинейное движение;
-
равномерное криволинейное движение; ,
-
криволинейное равнопеременное движение;
,
-
криволинейное равнопеременное движение;, - криволинейное движение с переменным ускорением.
Вопросы для самопроверки.
Что называется материальной точкой? Почему в механике вводят такую модель?
Что такое система отсчёта?
Что такое вектор перемещения? Всегда ли модуль вектора перемещения равен отрезку пути, пройденному точкой?
Дать определение векторов средней скорости и среднего ускорения, мгновенной скорости и мгновенного ускорения.
Что характеризует тангенсальная составляющая ускорения? Нормальная составляющая ускорения? Каковы их модули?
Возможны ли движения, при которых отсутствует нормальное ускорение? Тангенсальное ускорение? Приведите примеры.
Задачи.
Определить характер прямолинейного движения точки по заданному закону движения:
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() .
.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
По данным предыдущего вопроса вычислите все кинематические характеристики движения точки для момента времени t = 2 c , приняв s в метрах.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Точка движется по окружности радиуса r = 4 м по закону
 (s
– в
метрах, t
– в секундах). Найти модуль
ускорения точки и угол
(s
– в
метрах, t
– в секундах). Найти модуль
ускорения точки и угол
 между вектором ускорения и вектором
скорости в тот момент
,
когда скорость равна 6 м /с.
между вектором ускорения и вектором
скорости в тот момент
,
когда скорость равна 6 м /с.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4.
Точка движется по окружности, радиус
которой
![]() =200
м, с касательным ускорением
=200
м, с касательным ускорением
![]() .
Определить угол в градусах между
векторами скорости и полного ускорения
точки в момент времени, когда её скорость
.
Определить угол в градусах между
векторами скорости и полного ускорения
точки в момент времени, когда её скорость
![]() .
.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5. По окружности радиуса
![]() движется точка согласно уравнению
движется точка согласно уравнению
![]() .
Определить полное ускорение точки в
момент времени
.
Определить полное ускорение точки в
момент времени
![]() .
.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
