Тема 1. 5. Произвольная пространственная система сил.

1.5.1. Пространственная система сходящихся сил.

1.5.2. Момент силы относительно оси.

1.5.3. Условия равновесия системы сил, как угодно расположенных в пространстве.

1.5.1. Система сил, линии действия которых расположены в различных плоскостях, называется пространственной системой сил. Пространственная система сил называется сходящейся, если линии действия всех сил системы пересекаются в одной точке. Аналогично плоской системе (см. стр. 15, п. 1.4.2.) сил её можно свести к системе сил, приложенных в одной точке и сложить по правилу многоугольника. Следует отметить, что силовой многоугольник пространственной системы сил не лежит в одной плоскости, поэтому для нахождения равнодействующей чаще применяется аналитический метод, а не графический.

Аналитическое определение равнодействующей системы сходящихся сил, т.е. определение модуля и направления искомого вектора путём вычисления, основано на применении метода проекции.

Проекция равнодействующей системы сходящихся сил на какую-либо ось равна алгебраической сумме проекций составляющих сил на эту ось:

(1.5.1.)

где - проекции, соответственно, сил на ось Ox; - проекции, соответственно, сил на ось Oy, - проекции, соответственно, сил на ось Oz.

Модуль равнодействующей пространственной системы сходящихся сил определяется формулой

(1.5.2.)

Углы между равнодействующей и координатными осями, а следовательно, и направление равнодействующей определяется формулами

(1.5.3.)

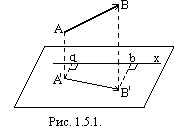
Примечание. Для нахождения проекции вектора (вектора ) на ось (ось х ), не лежащую с ним в одной плоскости, иногда бывает удобнее спроецировать сначала этот вектор на плоскость (рис. 1.5.1.), в которой лежит данная ось, а затем уже найденную проекцию (проекция ) вектора на плоскость спроецировать на данную ось (способ двойного проецирования). Проекция вектора (проекция ) на ось есть скалярная алгебраическая величина. Проекция же вектора на плоскость есть величина векторная и, следовательно характеризуется не только своим значением, но и направлением на плоскости проекции.

Если пространственная система сходящихся сил находится в равновесии, то равнодействующая этой системы сил равна нулю, а следовательно, равны нулю и проекции равнодействующей

Отсюда вытекают следующие условия равновесия пространственной системы сходящихся сил: для равновесия пространственной системы сходящихся сил необходимо и достаточно, чтобы алгебраическая сумма проекций всех сил на каждую из трёх координатных осей равнялась нулю.

1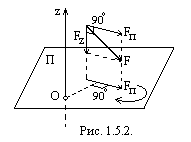 .5.2. Прежде чем перейти к рассмотрению условий равновесия пространственной системы произвольно расположенных сил, дадим определение момента силы относительно оси.

Моментом силы относительно какой-либо оси называется величина, характеризующая вращательный эффект данной силы относительно этой оси. Момент силы относительно оси равен моменту проекции этой силы на плоскость (рис. 1.5.2.), перпендикулярную к данной оси, относительно точки пересечения оси с плоскостью:

.

Тот или иной знак в этой формуле определяется по следующему правилу: если для наблюдателя, смотрящего на плоскость П с положительной стороны оси z, проекция силы на плоскость П представляется вращающейся вокруг оси z против часовой стрелки, то момент считается положительным (рис. 1.5.2.); в противном случае его считают отрицательным.

Заметим, что

1. момент силы относительно данной оси не изменяется при перенесении силы вдоль её линии действия;

2. момент силы относительно оси равен нулю, если линия действия силы и ось лежат в одной плоскости.

1.5.3. Способ приведения сил к одному центру, рассмотренный в п. 1.4.2. (стр. 18) для плоской системы сил, вполне применим и для системы сил, расположенных как угодно в пространстве. Используя теорему Пуансо, можно любую пространственную систему сил заменить одной силой, равной главному вектору системы и приложенной в произвольной точке О, и парой, момент которой равен главному моменту данной системы сил относительно той же точки:

Для равновесия системы сил, расположенных как угодно в пространстве, необходимо и достаточно, чтобы равнялись нулю как главный вектор этой системы, так и её главный момент относительно произвольно выбранного центра приведения. Этим условиям можно придать и более удобную для практических целей аналитическую форму:

Для равновесия пространственной системы произвольно расположенных сил необходимо и достаточно, чтобы алгебраическая сумма проекций всех сил на каждую из трёх осей координат была равна нулю и чтобы алгебраическая сумма моментов всех сил относительно каждой из осей была равна нулю.

Заметим, что при составлении уравнений моментов нет необходимости в том, чтобы оси, относительно которых берутся моменты сил, совпадали с осями проекций. Для простоты решения уравнений рекомендуется ось проекций располагать перпендикулярно к линии действия одной из неизвестных сил, вследствие чего проекции этой силы исключаются из соответствующего уравнения проекций. Ось моментов рекомендуется выбирать лежащей в плоскости одной из неизвестных сил. Тогда момент этой силы относительно данной оси равен нулю. Одним словом, оси всегда нужно выбирать так, чтобы в каждое из шести уравнений равновесия вошло возможно меньшее число неизвестных.