МагнитнОе поле в Веществе. Задача 1
В ОМП с индукцией
помещена бесконечная плоскопараллельная
пластина из однородного и изотропного
магнетика с проницаемостью μ.
Пластина расположена перпендикулярно
к линиям
.
Определить магнитную индукцию
и напряженность магнитного поля
в магнетике.
[
,
,
где
- напряженность внешнего магнитного
поля]
Указания по решению.
Запишем условие соленоидальности магнитного поля:
.
В качестве замкнутой поверхности S выберем цилиндр, образующие которого параллельны силовым линиям поля (рис. ). Тогда интеграл можно представить в виде суммы 3-х интегралов (по боковой поверхноти и по каждому из оснований):
.
Отсюда ясно, что магнитная индукция поля в магнетике равна магнитной индукции внешнего поля:
.
Напряженность магнитного поля в магнетике найдем через ее связь с магнитной индукцией:
и
отсюда
.
Задача 2
В тонком тороидальном соленоиде с радиусом средней линии R и числом витков N сделан тонкий воздушный зазор толщиной d<<R. Магнитная проницаемость сердечника равна μ. Найдите напряженность и индукцию магнитного поля в сердечнике и зазоре, если по обмотке протекает ток I.
Указания по решению.
В этой задаче мы
имеем дело с неоднородной средой
«сердечник-зазор», поэтому вместо
теоремы о циркуляции вектора
необходимо применять закон полного
тока:
,
где L – средняя линия тора, охватывающая N токов I.
Разложим записанный интеграл на сумму двух интегралов по каждой из областей (сердечник и зазор) в отдельности:
.
Т.к. соленоид по условию тонкий, то можно принять, что поле внутри него однородно, тогда закон полного тока запишется в виде
,
здесь мы учли, что
выбранный контур совпадает с силовой
линией, а значит в любой точке векторы
напряженности поля и элемента длины
сонаправлены (
).
Для получения второго независимого равенства, рассмотрим границу раздела сред и воспольземся условием соленоидальности магнитного поля:
.
Запишем связь между индукцией и напряженностью поля:
или
т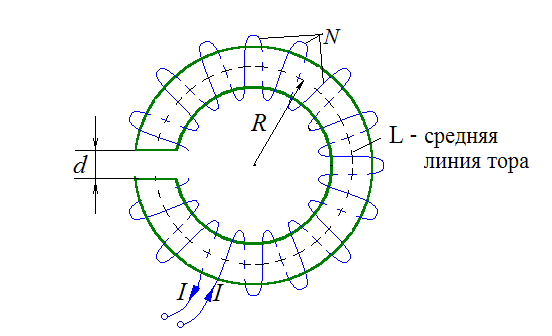
.к.
в зазоре
.
Подставляем в закон полного тока:
,
.
Значения же магнитной индукции будут одинаковыми и в сердечнике и в зазоре:
.
Задача 3
Соленоид длиной l=20 см, площадью поперечного сечения S=10 см2 и общим числом витков N=400 находится в диамагнитной среде. Определить силу тока I в обмотке соленоида, если его индуктивность L=1 мГн и намагниченность Рm= 20 А/м внутри соленоида. [2,09 А]
Указания по решению.
Намагниченность вещества пропорциональна величине намагничивающего поля:
,
где
- магнитная восприимчивость вещества,
т.е. для диамагнетика
.
Учитывая, что
,
запишем
.
По закону полного тока имеем
.
Отсюда сила тока с учетом выражения для напряженности будет равна
.
Осталось найти магнитную проницаемость вещества. Для этого воспользуемся выражением для индуктивности соленоида:
.
Завершите решение задачи самостоятельно и сравните ответ.
Задача 4
В ОМП вносится длинный вольфрамовый стержень (магнитная проницаемость вольфрама μ=1,017). Найдите, какая доля суммарного магнитного поля в этом стержне определяется молекулярными токами. [1,7 %]
Указания по решению.
Поле в стержне
складывается из внешнего поля
и поля микротоков
:
,
тогда искомая доля запишется так:
.
Для получения доли в процентах необходимо последнее выражение еще умножить на 100%.