Постановка задачи 4

1. Нахождение Y теоретического. Преобразование формулы и решение ее с помощью Метода Эйлера. 6

2. Моделирование метода оптимизации. 10

МЕТОД ПОКООРДИНАТНОГО СПУСКА 10

2.1. Описание метода поиска 10

2.2. Результаты работы программы: 11

3. Шум. 18

4. Целевая функция. 24

Список использованных источников 28

ПРИЛОЖЕНИЕ 29

Содержание

Постановка задачи 4

1. Нахождение y теоретического. Преобразование формулы и решение ее с помощью Метода Эйлера. 6

2. Моделирование метода оптимизации. 10

2.1. Описание метода поиска 10

2.2. Результаты работы программы: 11

3. Шум. 18

4. Целевая функция. 24

Список использованных источников 28

ПРИЛОЖЕНИЕ 29

Постановка задачи

В нашей работе нам нужно создать модель, которая будет удовлетворять исходным данным и сможет найти оптимальные параметры для идентификации исходной функции. Результатом работы должны быть графики поиска минимума значения функции, гистограмма распределения точек генератора случайных чисел, а также график Y теоретического, Y экспериментального от времени.

Моделирование используется, если эксперимент с реальным объектом:

1. опасный

2. дорогой

3. долговременный/краткосрочный

4. невозможный/трудный

Условная схема моделирования:

Т. к. у нас отсутствует объект, то мы заменяем его на Y теор. + шум

Y эксп. = Y теор. + шум

1. Нахождение y теоретического. Преобразование формулы и решение ее с помощью Метода Эйлера.

Здесь нам нужно найти значения функции Y теоретического, для того, чтобы потом получить Y экспериментально, с помощью шума.

Используя метод введения дополнительной переменной, получим:

Перейдём в вещественную форму:

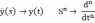
Обозначим:

Получим систему уравнений в канонической форме:

Далее решаем систему методом Эйлера. Начальные условия:

А также, на каждом шаге подставив полученные значения, рассчитываем

Выберем шаг h=0.5, выполним необходимые вычисления и построим график функции.

Полученный график представлен на рис.1. По графику видно, что функция

y(t)-> к числу чуть больше 0. А выходит она из точки ~ -1500. Узнаем точные значения этих точек. Для этого вычислим пределы:

= 30

= -1500

Некоторые значения y представлена в таблице 1 “ Зависимость значения функции от времени”.

Наилучший период наблюдения t=1...300, шаг h=0.5.

Взято 300 точек, т.к. уже на этом периоде наблюдения видно как график функции сходится к положительному числу около 0. График функции искажается при шаге больше 0.5 (при шаге больше 0,8 - расходится). А при меньшем шаге сходимость получим за большее число шагов. Поэтому выбран шаг h=0.5.

(рис.1)

Таблица 1

“Зависимость значения функции от времени”

t	y(t)
1	-1500,000
11	1130,336
21	-407,472
31	-131,811
41	546,368
51	-554,815
61	465,039
71	-156,678
81	-15,510
91	218,653
101	-192,945
111	201,441
121	-48,697
131	18,974
141	98,544
151	-54,763
161	97,352
171	-2,843
181	28,262
191	54,751
201	-2,138
211	56,381
221	16,410
231	30,295
241	38,875
251	17,849
261	40,304
271	24,418
281	30,484
291	33,157