16. Что называется зарядной мощностью линии и как она определяется?

Под действием приложенного к линии переменного напряжения в емкости линии возникает переменное электрическое поле и возникает реактивный ток. Этот ток называется емкостным или зарядным током линии.

(2.1.1)

Зная емкостной ток линии, можно определить емкостную или зарядную мощность линии.

(2.1.2)

где U – рабочее линейное напряжение, кВ.

17 Как определяются потери мощности и энергии в линиях?

(a)Потери мощности и энергии в линиях

1. Как известно из ТОЭ, потери активной и реактивной мощностей в линиях трехфазного переменного тока, если пренебречь проводимостями,

где R и X — активное и индуктивное сопротивление; Iа и Iр— значения активной и реактивной составляющих пол­ного тока I.

где U— линейное напряжение сети.

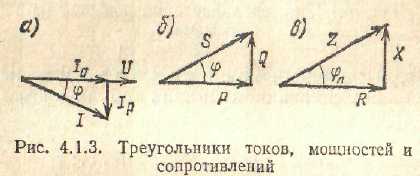
Треугольники токов, мощностей и сопротивлений изображены на рис. 2.2.1, а, б, в. Известно также, что активная и реактивная мощ­ности

Если выразить значение тока через его активную Iа и реактивную Ip составляющие (рис. 2.2.1, а) и заменить в (2.2.2) и , а затем выразить значения

Iа и Iр через мощности Р и Q и подставить найденные вы­ражения в (2.2.1), то получим одно из важнейших выра­жений для электрических сетей:

где S — полная мощность согласно рис. 2.2.1,6.

Рассмотрим физическую сущность этих выражений и сделаем основные выводы.

А. Потери как активной, так а реактивной мощности зависят и от Р, и от Q

Б. Потери обратно пропорциональны квадрату напря­жения. Поэтому даже незначительное повышение напряже­ния дает значительное снижение потерь мощности. Однако повышение напряжения вызывает дополнительный расход средств. Например, линии 500 кВ значительно дороже линий 220 кВ. Чтобы повысить напряжение специальными устройствами, требуются также дополнительные средства. Поэтому напряжение выбирается экономическим сравне­нием вариантов.

2. Потери мощности при нескольких нагрузках находятся суммированием потерь на каждом участке (рис.2.2.2), т. е.

3. Потери мощности при равномерно распределенной нагрузке в 3 раза меньше, чем при той же нагрузке, сосре­доточенной в конце линии.

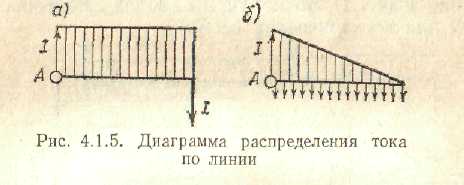
Рассмотрим график тока при нагрузке в конце линии (рис. 2.2.3, а) и при равномерно-распределенной нагрузке (рис. 2.2.3, б). Как видно из рисунков, ток при равномерно распределенной нагрузке снижается. Естественно, что и потери мощности в этом случае будут меньше.

4. Наиболее распространенной является трехфазная система. Она применяется для создания вращающегося магнитного поля, т. е. для возможности применения про­стых электродвигателей. Кроме того, в трехфазной системе меньшие потери мощности. Потери мощности в однофазной системе при тех же мощности S и напряжении U больше в 2 раза. Однако в однофазной системе два про­вода, в то время как в трехфазной — три. Для того чтобы расход металла был тем же, нужно уменьшить сечение про­водов трехфазной линии по сравнению с однофазной в 1,5 ра­за. Во столько же раз будет больше сопротивление, т. е. . Подставляя это значение в выражение для DP₁ , получим

т. е. потери активной мощности в однофазной линии в 2/1,5—1,33 раза больше, чем в трехфазной.

2.2.(б) Потери энергии в линиях.

Так как мощность — это есть энергия в единицу времени, то потери энергии ДЗ — это потери мощности, умноженные на время:

Однако потери мощности ЛР остаются постоянными только в том случае, если ток не меняется. В действитель­ности, как указывалось, ток меняется всегда для каждого объекта.

Если изобразить годовой график нагрузок отвлеченного потребителя, как показано на рис. 2.2.4., то годовые потери энергии будут пропорциональными площади графика квадратичных нагрузок и могут быть выражены как

где Т — время включения потребителя

В данном случае потребитель включен в течение всего года, т. е. T=8760 ч. Однако ток I от времени Т математи­чески выразить нельзя. Поэтому используют различные ис­кусственные способы.

Каждая группа потребителей (машиностроительные по­требители, текстильные фабрики и т. д.) имеет характерные графики нагрузок. Нагрузки отдельных подстанций и ли­ний складываются из нагрузок потребителей и также име­ют характерные графики.

Чтобы определить площадь какого-либо графика, надо заменить его группой прямоугольников, примерно состав­ляющих фактический график потребителя, а затем способами, изложенными далее, определить площадь этих графиков и соответственно потери энергии.

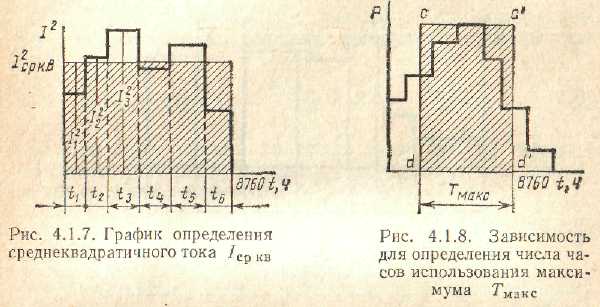
Среднеквадратичный ток. Одним из при­меров определения потерь энергии потребителя является определение среднеквадратичного тока Iср кв (рис. 2.2.5), т. е. такого тока, который, все время протекая по линии, даст те же потери, что и действительные токи, иначе пря­моугольник, очерченный линиями, должен быть равен дей­ствительной площади данного графика. Тогда

Найдя величину , потери энергии можно определить по выражению

Число часов использования макси­мума Тмакс и время максимальных потерь t. Наиболее распространенным методом определения потерь

энергии является метод с использованием времени мак­симальных потерь t.

На рис. 2.2.6 показана зависимость передаваемой мощ­ности Р от времени t. Известно, что потребитель какую-то

часть времени работает с максимальной нагрузкой Pмакс. Время, в течение которого, работая с максимальной нагруз­кой , он взял бы из сети энергию, равную энергии действительно полученной потребителем за год, и называ­ется числом часов использования максимума Тмакс. Эта энергия определяется площадью прямоугольника cc'd'dc, т. е.

Аналогично (рис, 2.2.7), время, в течение которого потре­битель, работая с максимальными потерями , вы­зовет такие же потери энергии, которые имеют место в дей­ствительности, называется временем максимальных потерь т. Эти потери определяются площадью прямоугольника ee'f'fe, т. е.

Значения Тмакс и t зависят только от графика нагрузок.

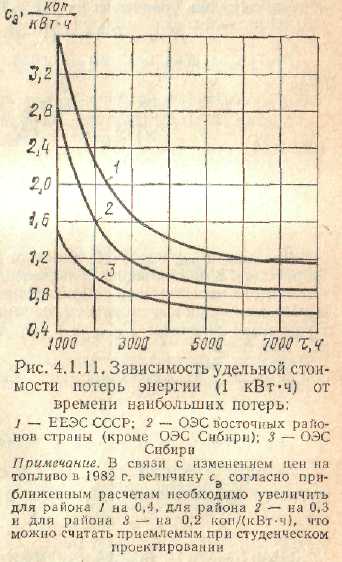
Время потерь t так­же зависит от характера потребителя. Поэтому для типовых графиков нагрузок можно устано­вить зависимость f(Tмакс), которая при­ведена на рис. 2.2.8. Таким образом, для ти­повых графиков нагру­зок, зная величину Тмакс (усредненную или фак­тическую потребителя), можно найти значение т по рис. 2.2.8 и потери энергии по (2.2.15), а также удельную стои­мость потерь энергии с_э , в зависимости от t. (рис. 2.2.9).

18 Как проводится расчет сетей со стальными проводами? Очень часто в сельских сетях, питающих небольшие населенные пункты или железнодорожные объекты (например, линии автоблокировки), а также в сетях местного назначения с малой плотностью нагрузки провода из цветного металла используются недостаточно. Это получается, когда сечение медного или алюминиевого провода выбирают не по потере напряжения или допустимому току нагрузки, а по механической прочности и завышают до минимального разрешаемого сечения для воздушных линий.Так, для воздушных линий напряжением 6 кВ ПУЭ допускают минимальное сечение алюминиевых проводов А-25 (см. табл. 1). Предположим, например, что по линии напряжением 6 кВ необходимо передать на расстояние 12 км мощность P=50 кВт при cosф=0.8 ( Q=37.5 квар). При r0= 1.14 Ом/км и x0=0.377 Ом/км для провода А-25 получаем потерю напряжения, выраженную в процентах:

,

что значительно меньше 10%, допустимых для сетей сельского назначения. Видно, что принятый минимально возможный по механическим соображениям провод А-25 использован весьма мало, так как в данном случае по допустимой потере напряжения мог бы быть применен алюминиевый провод сечением 6 мм2. Так как это невозможно, то в подобных случаях целесообразно алюминиевые провода заменять стальными, имеющими большую механическую прочность, но более низкие электрические характеристики. Применение стальных проводов позволяет снизить затраты на сооружение линии и, главное, заменить дефицитный провод из цветного металла стальным, менее дефицитным.

Расчет сетей со стальными проводами выполняют в такой последовательности: определяют расчетные токи участков линии, затем намечают для каждого участка один или два возможных варианта сечений проводов (однопроволочных или многопроволочных), выбирая их по таблицам допустимых токов по нагреву. Далее определяют сопротивления и для каждого участка. Активное сопротивление и внутреннее реактивное сопротивление определяют в зависимости от величины тока, протекающего по данному участку, а внешнее реактивное сопротивление - в зависимости от геометрических размеров линии. После этого определяют потерю напряжения по формуле:

(1)

и ответ сравнивают с допустимой потерей.

Следует отметить, сечения стальных проводов, выбранные по допустимым токам нагрузки, приводят, как правило, к чрезмерно большим потерям напряжения. Убедившись в этом, увеличивают намеченные сечения и вновь проверяют потери напряжения. Окончательный выбор сечения проводов достигается рядом последовательных приближений.

Выбор стальных проводов по экономической плотности тока не практикуется.