
Содержание
Практическая часть 3
Задача №1 3
Задача №2 7
Задача №3 9
Задача №4 12
Задача №5 13
Задача №6 14
Список литературы 16
Практическая часть Задача №1
Имеются следующие выборочные данные (выборка 10%-ная, механическая) о выпуске продукции и сумме прибыли, млн.руб.:
№ Предприятия |
Выпуск продукции |
Прибыль |
№ Предприятия |
Выпуск продукции |
Прибыль |
1. |
65,0 |
15,7 |
16 |
52,0 |
14,6 |
2. |
78.0 |
18,0 |
17 |
62,0 |
14,8 |
3. |
41,0 |
12,1 |
18 |
69,0 |
16,1 |
4. |
54,0 |
13,8 |
19 |
85,0 |
16,7 |
5. |
66,0 |
15,5 |
20 |
70,0 |
15,8 |
6. |
80,0 |
17,9 |
21 |
.71,0 |
16,4 |
7. |
45,0 |
12,8 |
22 |
64,0 |
15,0 |
8. |
57,0 |
14,2 |
23 |
72,0 |
16,5 |
9. |
67,0 |
15,9 |
24 |
88,0 |
18,5 |
10. |
81,0 |
17,6 |
25 |
73,0 |
16,4 |
П. |
92,0 |
18,2 |
26 |
74,0 |
16,0 |
12. |
48,0 |
13,0 |
27 |
96,0 |
19,1 |
13. |
59,0 |
16,5 |
28 |
75,0 |
16,3 |
14. |
68,0 |
16,2 |
29 |
101,0 |
19,6 |
15. |
83,0 |
16,7 |
30 |
76,0 |
17,2 |
По исходным данным:
1. Постройте статистический ряд распределения предприятий по сумме прибыли, образовав пять групп с равными интервалами. Постройте графики ряда распределения. .
2. Рассчитайте характеристики ряда распределения предприятий по сумме прибыли: среднюю арифметическую, среднее квадратическое отклонение, дисперсию, коэффициент вариации. Сделайте выводы.
3. С вероятностью 0,954 определите ошибку выборки для средней суммы прибыли на одно предприятие и границы, в которых будет находиться сумма прибыли одного предприятия в генеральной совокупности.
4. С вероятностью 0,954 определите ошибку выборки для доли предприятий со средней прибылью свыше 16,6 млн. руб. и границы, в которых будет находиться генеральная доля.
Решение
Шаг интервала
![]() = (19,6-12,1)/5=1,5 млн.руб.
= (19,6-12,1)/5=1,5 млн.руб.
Результаты группировки представим в виде таблицы 1
Таблица 1
Группы предприятий по сумме прибыли, млн.руб. |
12,1-13,6 |
13,6-15,1 |
15,1-16,6 |
16,6-18,1 |
18,1-19,6 |
Центры интервалов |
12,85 |
14,35 |
15,85 |
17,35 |
18,85 |
Число предприятий |
3 |
5 |
12 |
6 |
4 |
Накопленные частоты |
3 |
8 |
20 |
26 |
30 |
Далее построим графики ряда распределения:
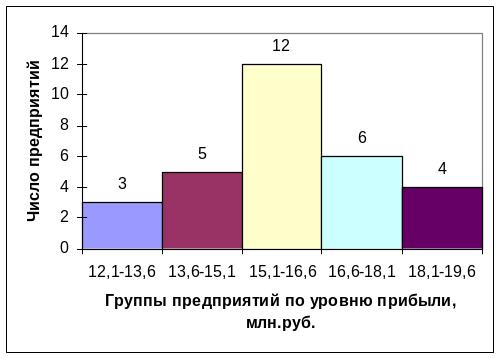
Рис. 1 Гистограмма

Рис.2 Полигон распределения

Рис. 3 Кумулята
С помощью статистических функций программы Excel рассчитаем характеристики ряда распределения предприятий по сумме прибыли:
Среднее |
16,10333333 |
Стандартная ошибка |
0,329069861 |
Медиана |
16,25 |
Мода |
16,5 |
Стандартное отклонение |
1,802389857 |
Дисперсия выборки |
3,248609195 |
Эксцесс |
0,007645016 |
Асимметричность |
-0,289843568 |
Интервал |
7,5 |
Минимум |
12,1 |
Максимум |
19,6 |
Сумма |
483,1 |
Счет |
30 |
Уровень надежности(95,4%) |
0,68604848 |
Коэффициента
вариации:
![]()
Вывод: в рассматриваемой выборочной совокупности предприятий средний размер прибыли составляет 16 млн.руб., стандартное отклонение от среднего значения индивидуальных значений составляет 1,8 млн.руб. Коэффициент вариации меньше 35%, что свидетельствует о том, что рассматриваемая совокупность предприятий весьма однородна и среднее значение прибыли является типичным для данной совокупности.
3. Определим ошибку выборки для средней суммы прибыли на одно предприятие:
а) средняя ошибка выборки:
![]()
б) предельная ошибка выборки
![]() млн.руб.
млн.руб.
Границы, в которых будет находиться сумма прибыли одного предприятия в генеральной совокупности:
![]() ,
,
16-0,58≤![]() ≤16+0,58
≤16+0,58
15,42≤ ≤16,58 млн.руб.
4. Определим долю предприятий со средней прибылью свыше 16,6 млн.руб.:
w=(4+6)/30=0,33
Средняя ошибка выборки для доли:
![]()
Предельная ошибка выборки для доли с вероятностью 0,954:
![]()
Доля предприятий со средней прибылью свыше 16,6 млн.руб. в генеральной совокупности будет находиться в следующих пределах:
w-Δ≤p≤w+Δ,
0,33-0,18≤p≤0,33+0,18
0,15≤p≤0,51.
