
Оглавление
1.Решение методом Лагранжа . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3
1.1.Седловая точка функции Лагранжа . . . . . . . . . . . . . . . . . . . . . . 7
1.2.Решение задачи квадрат. программирования методом седловой точки . . 7
1.3.Численный метод решения . . . . . . . . . . . . . . . . . . . . . . . . . . . 9
2.Теоретические вопросы . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 10
2.1.Активные и пассивные ограничения . . . . . . . . . . . . . . . . . . . . . . 10
2.2. |
Теорема Куна-Таккера . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 10 |
2.3.Достаточные условия минимума . . . . . . . . . . . . . . . . . . . . . . . . 10
2.4. |
Седловая точка . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
10 |
2.5. |
Метод седловой точки для задачи квадратичного программирования . . |
11 |
1.Решение методом Лагранжа
Дана задача минимизации L и ограничения G. |
|
|||||||||||||||
L : F (x1; x2) = min |
|
(x1 |
10)2 + 100 (x2 |
10)2 |
|
|||||||||||
|
|
1 + 3 2 6 |
|
|
|
|
||||||||||
|
82x1 |
+ 5x2 |
6 30; |
|
|
|
||||||||||
|
> |
|
x |
|
|
x |
|
|
|
12; |
|
|
|
|||
|
> |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
>3x1 + 2x2 6 22; |
|
|
|
||||||||||||
|
> |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
> |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
G : |
>x |
1 |
|
|
3x |
2 6 |
0; |
|
|
|
|
|
|
|||
|
> |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
> |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
> |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
> |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1) |
|
> |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
<2x1 + 5x2 |
|
|
10; |
|
|
|
|||||||||
|
>5x1 + x2 >>5; |
|
|
|
|
|
|
|||||||||
|
> |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
> |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
> |
|
|
|
|
0; |
|
x2 |
|
|
|
0 |
|
|
|
|
|
>x1 |
> |
|
> |
|
|
|
|||||||||
|
> |
|
|
|
|
|
|
|
|
|
|
|||||
>
>
>
>
>
:
Для наглядности далее приводится график функции.
Рис. 1: График функции
3
Представим ограничения в виде системы неравенств, где левая часть будет представлять собой x2
8
>1
|
> |
x |
|
6 |
|
|
x |
+ 4; |
|
||||||
|
|
|
|
|
|||||||||||
|
|
2 |
3 |
|
1 |
2 |
x1; |
|
|||||||
|
>x2 6 6 |
|
|
|
|
|
|||||||||
|
> |
|
|
|
|
|
5 |
|
|
|
|
|
|||
|
> |
|
|
|
|
|
|
|
|
|
|
||||
|
> |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
> |
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
> |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
> |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
>x2 |
|
11 |
|
|
|
|
x1; |
|
||||||
|
> |
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|||
|
> |
|
|
|
|
|
|
|
|
|
|
||||
|
> |
|
|
|
|
|
|
|
|
|
|
|
|||
G : |
> |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
> |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
> |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
> |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
>x2 |
> |
|
|
x1; |
|
|
|
|
|
|||||
|
3 |
|
|
|
|
|
|||||||||
|
< |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
>x |
|
> |
2 |
|
|
|
2 |
x |
|
; |
|
|||
|
2 |
|
|
|
|
|
|||||||||
|
> |
|
|
|
|
|
|
|
1 |
|
|
||||
|
> |
|
|
|
|
|
5 |
|
|
|
|
|
|||
|
> |
|
|
|
|
|
|
|
|
|
|
||||
|
> |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
> |
|
|
|
5 |
|
|
5x1; |
|
||||||
|
>x2 |
> |
|
|
|
||||||||||
|
> |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
> |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
> |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
> |
|
|
|
0; |
|
|
x2 |
|
|
0 |
||||
|
>x1 |
> |
|
|
> |
||||||||||
|
> |
|
|
|
|
|
|
|
|
|
|
|
|||
|
> |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
>
>
>
>
:
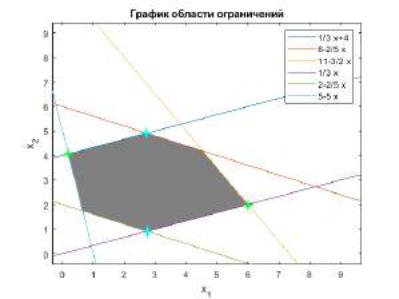
Построим графики и увидим область ограничений. На графике зелёными точками выделены ограничения на x1, синими на x2.
Приведём область ограничений к виду gi 6 0, где i = 1; : : : ; 8; так как x1 > 0 и x2 > 0, можно избавиться от этих ограничений в дальнейшем, так как остальные ограничения уже определены так же
|
82x1 + 5x2 |
|
|
30 |
6 0; |
||||||
|
> |
x1 + 3x2 |
12 |
6 |
0; |
||||||
|
|
|
|
|
|
|
22 |
|
0; |
||
|
>3x1 + 2x2 |
|
|
6 |
|||||||
M : |
> |
|
|
|
|
|
|
|
|
||
> |
|
|
|
|
|
|
|
|
|||
|
> |
|
|
|
|
|
|
|
|
|
|
|
> |
|
|
|
3x2 |
|
|
|
|
0; |
|
|
>x1 |
|
|
|
|
6 |
|||||
|
> |
|
|
|
|
|
|
|
|
|
|
|
< |
|
|
|
|
|
|
|
|
6 0; |
|
|
> 2x1 5x2 + 10 |
||||||||||
|
> |
|
5x1 |
|
x2 + 5 |
6 0 |
|||||
|
> |
|
|
||||||||
|
> |
|
|
|
|
|
|
|
|
|
|
|
> |
|
|
|
|
|
|
|
|
||
>
>
>
:
4
Функция Лагранжа выглядит следующим образом
= 0 (x1 10)2 + 100 (x2 10)2 + 1 ( x1 + 3x2 12) + 2 (2x1 + 5x2 30)+
(2)
+ 3 (3x1 + 2x2 22) + 4 (x1 3x2) + 5 ( 2x1 5x2 + 10) + 6 ( 5x1 x2 + 5)
Выписываем условия стационарности, дополняющей нежёсткости и неотрицательности
8200 0 |
(x2 |
|
|
10) + 3 1 + 5 2 |
+ 2 3 |
|
|
3 4 |
|
5 5 |
6 = 0; |
||||||||||||||
> |
2 0 |
(x1 |
|
10) |
|
1 + 2 2 |
+ 3 3 + 4 |
|
2 5 |
|
5 6 |
= 0; |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
> |
|
|
|
x1 + 3x2 |
|
|
12) = 0; |
|
|
|
|
|
|
|
|
|
|
||||||||
> 1 ( |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
> |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
> |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
> |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
> |
|
|
|
|
|
|
|
|
|
|
|
|
|
30) = 0; |
|
|
|
|
|
|
|
|
|
|
|
> 2 (2x1 + 5x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
> |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
> |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
> |
|
(3x |
+ 2x |
|
|
|
22) = 0; |
|
|
|
|
|
|
|
|
|
|
||||||||
> |
2 |
|
|
|
|
|
|
|
|
|
|
|
(3) |
||||||||||||
> |
3 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
> |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
> |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
> |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
< 4 (x1 |
|
|
3x2) = 0; |
|
|
|
|
|
|
|
|
|
|
||||||||||||
> 5 |
( |
|
2x1 |
|
|
|
5x2 + 10) = 0; |
|
|
|
|
|
|
|
|
|
|||||||||
> |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
> |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
> |
|
|
|
|
|
|
|
|
|
x2 + 5) = 0; |
|
|
|
|
|
|
|
|
|
|
|||||
> 6 ( 5x1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
> |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
> |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
> |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
> |
|
|
|
|
|
|
|
|
1 > 0; 2 > 0; |
3 > 0; |
|
4 > 0; |
5 > 0; 6 > 0 |
||||||||||||
> 0 > 0; |
|
|
|
|
|||||||||||||||||||||
> |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
>
>
>
>
>
:
Задача Куна-Таккера выглядит следующим образом; так как градиенты функции Лагранжа линейно независимы, выполняется условие регулярности, поэтому 0 = 0:5.
8100x2 |
+ 3 1 |
+ 5 2 + 2 3 |
|
3 4 |
|
|
5 5 |
6 |
|
1000 = 0; |
|
||||||||||||||||||||||
> |
x1 |
|
1 |
+ 2 2 |
|
+ 3 3 + 4 |
2 5 |
|
5 6 |
10 = 0; |
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
x1 + 3x2 |
|
|
|
12) = 0; |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
> 1 ( |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
> |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
> |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
> |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
> |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
30) = 0; |
|
|
|
|
|
|
|
|
|
|
|
|
|||
> 2 (2x1 + 5x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
> |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
> |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
> |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
> |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
22) = 0; |
|
|
|
|
|
|
|
|
|
|
|
|
|||
> 3 (3x1 + 2x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
> |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
> |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
> |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
> |
|
|
|
|
|
|
|
|
|
3x2) = 0; |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
> 4 (x1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
> |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
> |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
> |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
> |
|
|
|
|
|
|
2x1 |
|
|
|
5x2 + 10) = 0; |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
> 5 ( |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
> |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
> |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
> |
|
|
( 5x |
|
|
|
|
x |
|
+ 5) = 0; |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
> |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(4) |
|||||||||||||||
> |
6 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
> |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
> |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
> |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
< x1 + 3x2 12 6 0; |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
>2x1 + 5x2 |
|
30 6 0; |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
> |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
> |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
> |
|
|
|
|
|
|
|
|
|
|
|
|
|
22 |
|
|
|
0; |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
>3x1 + 2x2 |
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
> |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
> |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
> |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
> |
|
|
|
|
|
3x2 6 0; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
>x1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
> |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
> |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
> |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
> |
|
2x1 |
|
|
5x2 + 10 6 0; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
> |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
> |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
> |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
> |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
> |
|
5x |
1 |
|
|
x |
|
+ 5 |
6 |
0; |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
> |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
> |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
> |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
> |
|
|
|
|
|
|
0; |
|
|
2 |
|
|
|
0; 3 |
|
0; |
4 |
|
|
0; |
5 |
|
0; |
6 |
|
0 |
|||||||
> 1 |
> |
|
|
|
> |
> |
> |
> |
> |
||||||||||||||||||||||||
> |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
>
>
>
>
>
:
5
Для решения этой системы была составлена таблица в Excel. |
|
|||||||||
|
A |
B |
C |
D |
E |
F |
G |
H |
|
I |
1 |
|
Переменные |
|
|
|
Коэффициенты |
|
|||
2 |
x1 |
x2 |
0 |
1 |
2 |
3 |
4 |
5 |
|
6 |
3 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
0 |
4 |
Условия стационарности |
|
|
|
Ограничения |
|
||||
5 |
f1 |
f2 |
|
g1 |
g2 |
g3 |
g4 |
g5 |
|
g6 |
6 |
A6 |
B6 |
|
D6 |
E6 |
F6 |
G6 |
H6 |
|
I6 |
7 |
|
|
|
Условия дополняющей нежёсткости |
||||||
8 |
|
|
|
a1 |
a2 |
a3 |
a4 |
a5 |
|
a6 |
9 |
A9 |
1 |
|
D9 |
E9 |
F9 |
G9 |
H9 |
|
I9 |
Втаблице в ячейках обозначены следующие формулы:
A6: =2*C3*(A3-10)-1*D3+2*E3+3*F3+G3-2*H3-5*I3
B6: =200*C3*(B3-10)+3*D3+5*E3+2*F3-3*G3-5*H3-I3
D6: =-1*A3+3*B3-12 |
I6: =-5*A3-B3+5 |
G9: =G3*G6 |
E6: =2*A3+5*B3-30 |
A9: =B9 |
|
F6: =3*A3+2*B3-22 |
D9: =D3*D6 |
H9: =H3*H6 |
G6: =A3-3*B3 |
E9: =E3*E6 |
|
H6: =-2*A3-5*B3+10 |
F9: =F3*F6 |
I9: =I3*I6 |
Настройки поиска решения.
оптимизировать целевую функцию $A$9 до значения 1
изменяя ячейки переменных $A$2; $B$2; $D$2; $E$2; $F$2; $G$2; $H$2; $I$2
ограничения: $A$6:$B$6 = 0, $D$6:$I$6 6 0, $D$9:$I$9 = 0
сделать переменные без ограничений неотрицательными
метод: поиск решения нелинейных задач методом ОПГ
Решение: x |
* |
= |
|
2:727 4:909 |
|
|
* |
= |
89:256 |
48:264 . Найденная точка x |
* |
имеет активные |
|||
|
|
|
, |
|
|
||||||||||
ограничения |
g1 |
и |
g2 |
стационарности в данном случае выполнено, так как изначаль- |
|||||||||||
|
|
|
|
. Условие |
|
|
|
|
|
|
|
|
|
||
но присутствовало в системе. Количество ограничений соответствует количеству переменных,1;2 6= 0 выполнено условие минимума первого порядка. dg1;2 = 0; dg3;4;5;6 6 0 выполнено условие минимума второго порядка. из всего вышесказанного следует, что x * точка локального минимума.
6
