1.Нахождение экстремумов

Определение оптимума функции.

•находим первые частные производные функции

fx01 = 4x31 4x1x2 + 200x1 200 fx02 = 2x2 2x21

•приравниваем их к нулю, чтобы найти стационарные точки

• сокращаем первое уравнение на 4, второе на 2

• из второго уравнения видно, что x2 = x21, заменяем в первом уравнении x31 x31 + 50x1 50 = 0;

50x1 = 50; x1 = 1; x2 = 1

•стационарная точка найдена: (1; 1);

•находим Гессиан функции

fx001x1 = 12x21 4x2 + 200; fx001x2 = 4x1;

fx002x2 = 2; fx001x1 (1; 1) = 208;

fx001x2 (1; 1) = 4; fx002x2 (1; 1) = 2;

•определяем знак угловых миноров: 1 > 0, 2 > 0 ) гессиан положительно определён ) стационарная точка является точкой минимума;

•значение функции в точке минимума: f(1; 1) = 0.

3

Определение вогнутости и выпуклости функции.

•функция нескольких переменных выпукла вниз, когда для любой точки выполнены следующие неравнества

• составляем систему неравенств и решаем её

•очевидно, выпуклое вниз подмножество функции: x2 < x21 + 50;

•функция нескольких переменных выпукла вниз, когда для любой точки выполнены следующие неравнества

• составляем систему неравенств и решаем её

• очевидно, функция не имеет выпуклого вверх подмножества.

4

Определение овражности.

• Находим собственные числа гессиана в точке 1 1

(208 ) (2 ) = 0;

2 210 + 416 = 0; p

210 2102 4 416

• очевидно, cond H > 10 функция в окрестности точки 1 1 является овражной.

5

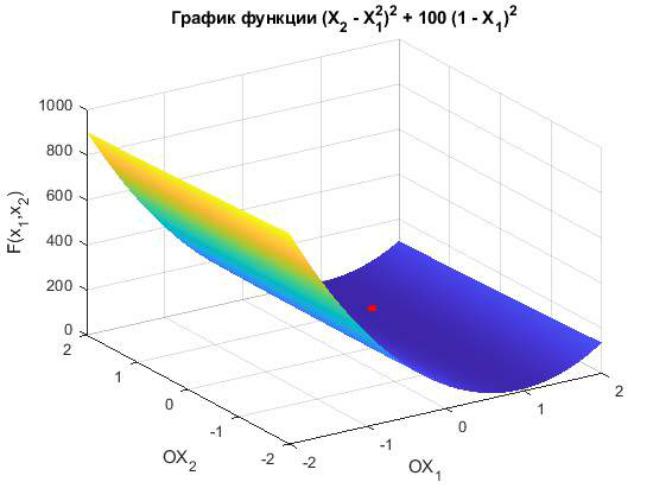
2.Построение графика

Для построения графика функции был выбран математический пакет MATLAB. Получившийся результат на рисунке 1. Красной точкой на рисунке обозначен минимум функции 1 1 . В приложении A описан скрипт для генерации такого графика.

Рис. 1: График функции 1 с точкой минимума

6