Лабораторная работа №4 Модель схемы компенсатора в LabView

1. Цель работы: изучить компенсационный метод с учетом погрешностей применяемых технических средств измерения.

2. Теория

Компенсационная схема имеет два источника питания: изменяемое напряжение U_x и опорное (образцовое) напряжение U₀ (рис.4.1).

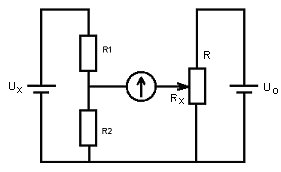
Рисунок 4.1 – Схема измерения напряжения компенсационным методом

Измеряемое напряжение, измененное делителем напряжения, будет равно

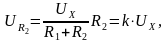
где k – коэффициент делителя напряжения, k = R₂/(R₁ + R₂).

Напряжение, снимаемое с потенциометра R, будет равно

где R_x – сопротивление между движком и нижним выводом потенциометра; R – полное сопротивление потенциометра.

Токи от двух источников питания направлены встречно. Следовательно, изменяя сопротивление R_x потенциометра, можно добиться равенства токов, а это возможно при условии

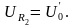
Тогда

(4.1)

Потенциометр (рис.4.2) состоит из кар­каса 1, на который намотан провод 2, изготовленный из материала с высоким удельным сопротивлением, и токосъемного движка 3, укреп­ленного на оси . Движок касается провода 2. В показанной конструкции контакт с подвижным движком осуществ­ляется с помощью неподвижного токосъемного кольца 4.

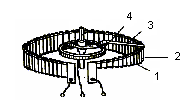
Рисунок 4.2 – Внешний вид потенциометра без корпуса

Для намотки используется проволока малого диаметра (константан, сплав платины, золота), так как чем меньше диаметр, тем меньше ступенчатость статической характеристики (рис.4.3).

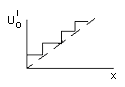
Рисунок 4.3 – Зависимость напряжения выхода потенциометра

от перемещения движка

Погрешность потенциометра обусловлена скачкообразным изменением сопротивления ΔR при переходе движка с одного витка на другой. Если в качестве номинальной функции преобразования принять функцию, проходящую посредине "ступенек", то максимальное значение приведенной погрешности, обусловленное дискретностью

δ_R = ±ΔR/(2R), (4.2)

где R - полное сопротивление преобразователя.

3. Порядок выполнения работы

1). Запустить программу LabVIEW и после открытия файла (Компенсационный метод.vi) должно появиться модель схемы (рис.4.4).

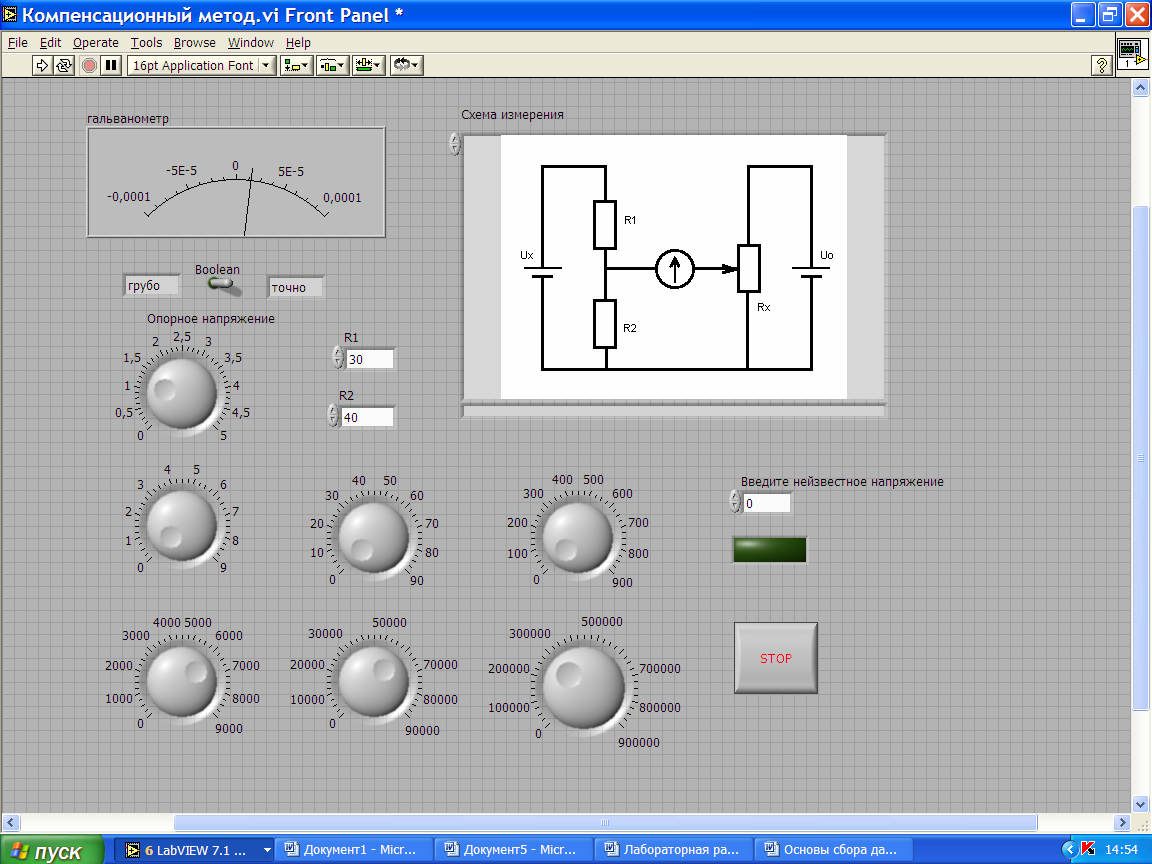
Рисунок 4.4 – Лицевая панель модели компенсатора

На схеме приведены: шкала гальванометра; переключатель с двумя положениями «грубо» (слева) и «точно» (справа), регулятор опорного напряжения, блок для ввода значений сопротивлений R₁ и R₂, кнопка «STOP». Кнопка «STOP» служит для выключения виртуального прибора.

2). Сопротивление потенциометра равно R = 1кОм. Набрать следующие данные: R₁ = 500 Ом и R₂ = 500 Ом (к = 0,5); U₀ = 5B и U_x = 4В.

3). Установить переключатель в положение «грубо» (влево) и изменяя сопротивление потенциометра R_x – магазин сопротивлений, добиться нулевого положения стрелки гальванометра. После чего необходимо перевести переключатель в положение «точно» (вправо) и произвести действия повторно.

Если компенсация достигнута, то загорается лампочка «Верно».

4. Задание

Рассчитать по формуле (4.1) неизвестное напряжение U_x с учетом того, что приведенная погрешность сопротивления потенциометра R = 1кОм равна δ_R = ±0,01%.

5. Содержание отчета

- цель работы;

- схема компенсатора;

- расчет напряжения U_x;

- выводы.

6. Контрольные вопросы

1) В чем заключается метод компенсации?

2) От чего зависит точность измерения компенсатора?

3) Какие достоинства компенсационного метода?

4) Какие основные недостатки?

5) Можно ли использовать потенциометр в качестве датчика угла?

6) Какие основные недостатки потенциометра?