3.1. Следы прямой

Прямая общего положения пересекает все три плоскости проекций.

Точку пересечения (встречи) прямой с плоскостью проекции называют следом прямой. Точка пересечения прямой 1 с горизонтальной плоскостью проекций называется горизонтальным следом прямой l_h, с фронтальной - фронтальным следом прямой l_v, с профильной - профильным следом прямой l_w (рис.3.1.).

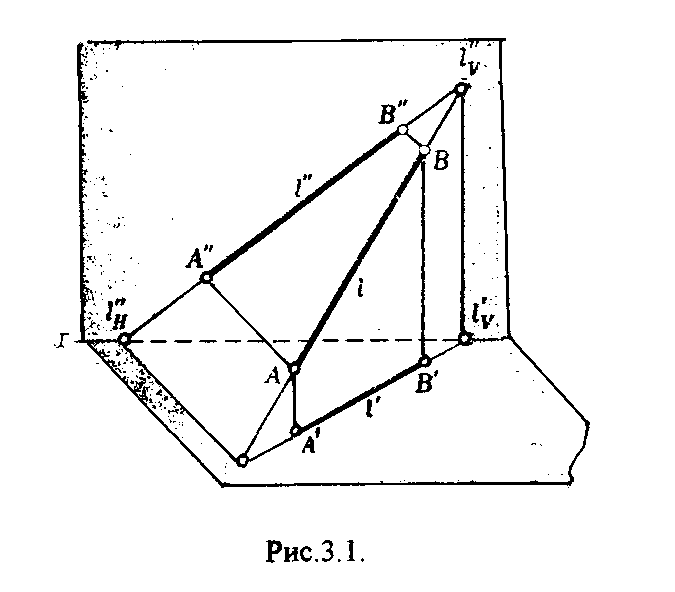
l_H, 1_H", 1_H, lv', lv", lv'", l_W', lw", lw'" - соответственно горизонтальная, фронтальная, профильная проекции следов 1_H, lv , lw. Очевидно, что 1_Н'= 1_H", lv"= lv , lw'"= l_W.

Чтобы построить на чертеже горизонтальный след прямой 1 (рис.3.2.), надо продолжить фронтальную проекцию прямой 1 до пересечения с осью х в точке 1н", затем, используя принцип принадлежности точки прямой достроить 1_Н'.

Для построения фронтального следа прямой 1 надо продлить горизонтальную проекцию прямой 1 до пересечения с осью х в точке lv' и достроить по соответствующим линиям связи l_V".

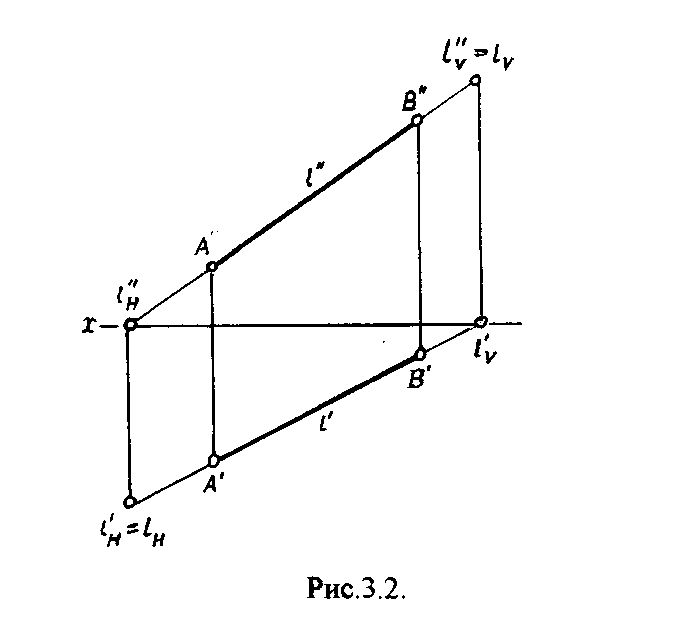
Аналогично строится профильный след прямой 1. Для этого продолжают либо фронтальную проекцию прямой I до пересечения с осью z в точке l_W", либо горизонтальную проекцию 1 до пересечения с осью у в точке l_W' и по соответствующим линиям связи достраивают недостающие проекции.

3.2. Прямые частного положения

Прямая может занимать по отношению плоскостям проекций частное положение:

а) параллельное плоскости проекции;

б) перпендикулярное плоскости проекции;

в) принадлежность плоскости проекции.

3.2.1. Прямые уровня

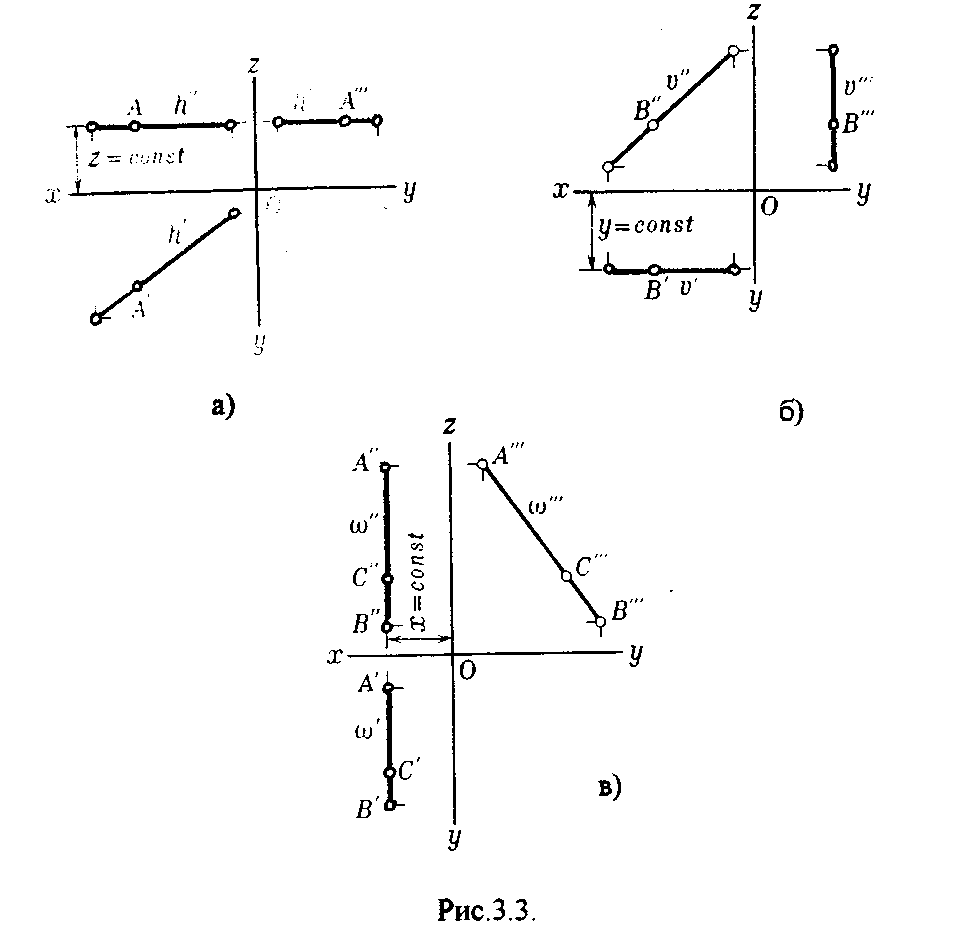
Прямые, параллельные плоскости проекций, называются прямыми уровня (рис.3.3.).

Горизонталь - прямая, параллельная горизонтальной плоскости проекций (рис.3.3.а.).

Фронталь - прямая, параллельная фронтальной плоскости проекций (рис.3.3.б.).

Профильная прямая - прямая, параллельная профильной плоскости проекций (рис.3.3.в.).

3.2.2. Проецирующие прямые

Прямые, перпендикулярные какой-либо плоскости проекции, называются проецирующими прямыми (рис.3.4.).

Прямые, перпендикулярные горизонтальной плоскости проекций, называются горизонтально — проецирующими прямыми (рис.ЗАа.).

Прямые, перпендикулярные фронтальной плоскости проекции, называются фронтально-проецирующими прямыми (рис.3.4.6.),

Прямые, перпендикулярные профильной плоскости проекций, называются профильно - проецирующими прямыми (рис.3.4.в.).

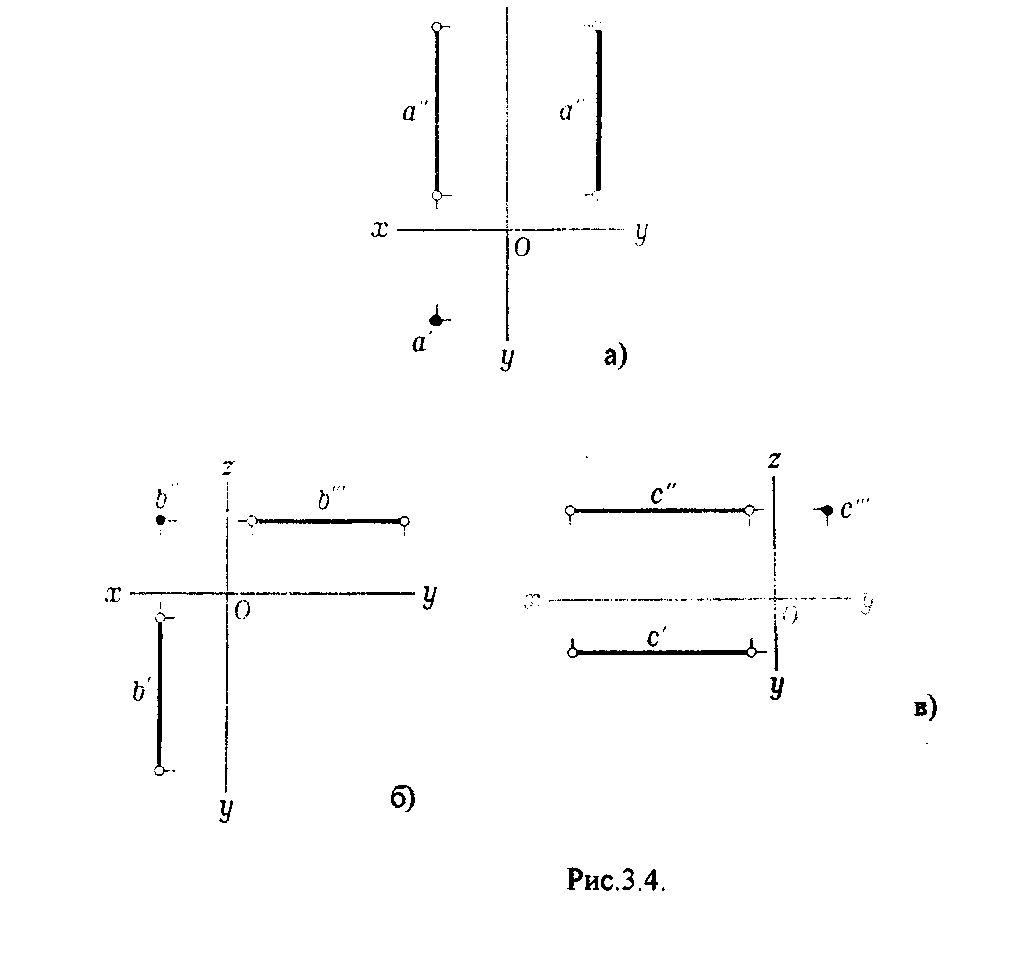
Октанты	Знаки координат
	X	У	z
I	+	+	+
II	+	—	+
III	+	-	—
IV	+	+	—
V	—	+	+
VI	-	-	+
VII	_	-	—
vni	-	+	-

3.2.3. Прямые, принадлежащие плоскости проекции

Это частный случай прямых уровня.

Характерным признаком таких прямых является принад-лежность двух проекций прямой координатным осям. На рис.3.5. показаны проекции прямых 1, т, п. Прямая 1 принадлежит горизонтальной плоскости проекции (рис.3.5.а.), прямая m –фрон-тальной плоскости проекции (рис.3.5.б.), прямая n -профильной плоскости проекции (рис. З.5.в.).