Цифровые сигналы Логические сигналы Логические функции Логические элементы И-НЕ, ИЛИ — НЕ, исключающие ИЛИ Основные законы и тождества алгебры логики Минимальный базис И — НЕ (ИЛИ — НЕ) Входы и выходы цифровых микросхем

Тема 6. Логические устройства. Цифровые сигналы

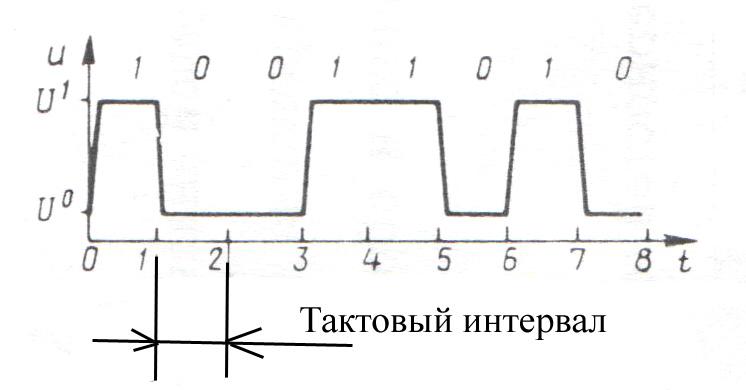
Цифровые устройства работают с цифровыми сигналами, которые могут принимать только два значения: от 0 до 0,5 В — уровень нуля или от 2,5 до 5 В — уровень единицы.  В отличие от аналоговых, цифровые сигналы, имеющие только два разращенных значения, защищены от действия шумов, наводок и помех. Небольшие отклонения от разращенных значений не искажают цифровой сигнал, так как существуют зоны допустимых отклонений. Кроме того, цифровые устройства проще проектировать и отлаживать.  Цифровым сигналом представляются двоичные числа, поэтому он состоит из элементов только двух различных значений. Одним из них представляется 1, а другим — 0. По установившейся терминологии эти элементы сигнала называют соответственно единицей и нулём.  Цифровой сигнал может быть потенциальным или импульсным.  Элементами потенциального цифрового сигнала являются потенциалы двух уровней. Каждый уровень остаётся неизменным в течении так называемого тактового интервала; на его границе уровень потенциала изменяется, если следующая цифра двоичного числа отличается от предыдущей. На рисунке изображён потенциальный цифровой сигнал, представляющий написанное сверху число; высоким потенциалом отображается 1, а низким — 0. 

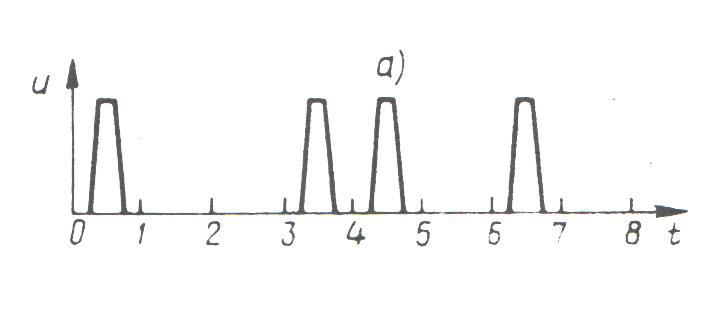
Элементами импульсного цифрового сигнала являются импульсы неизменной амплитуды и их отсутствие. На рисунке положительный импульс представляет 1, а отсутствие импульса представляет 0 написанного сверху двоичного числа. 

Логические сигналы

Наряду с цифровыми сигналами в цифровых устройствах действуют сигналы, появление которых связано с наступлением или не наступлением какого — либо события. Наличие или отсутствие таких сигналов и порождающие их условия связаны выражениями типа «если..., то ....» и другими логическими связями.  Поэтому такие сигналы называются логическими. Это название связано с тем, что аналогичные условия между причиной и следствием являются предметом обсуждения и изучения в логике.  Формальная логика — наука о законах и формах человеческого мышления — оперирует с высказываниями вне зависимости от их содержания, учитывая только их истинность или ложность. Истинные высказывания: «Электрический ток существует только в замкнутой цепи», «Архангельск расположен в северном полушарии», ложные: «Кит — теплолюбивое растение» «Ангара — приток волги».  Высказывания могут быть простыми и сложными. Простое содержит только один факт, не зависящий от других фактов, т. е. сам о себе может быть истинным или ложным. В приведенных выше примерах высказывания — простые. Сложные высказывание содержит несколько простых высказываний, например: «Я пойду в кино, если не будет дождя и со мной пойдёт приятель». Введения в формальную логику ограниченного числа логических связок (они будут далее), допускающих строго определённое толкование, позволило однозначно представлять сложное высказывание совокупностью простых, а введением символов, обозначающих простые высказывания, — решать логические задачи математическими средствами. Их совокупность составляет содержание алгебры и логики, или булевой алгебры, названной так в честь её создателя — английского математика Джорджа Буля. В соответствии с ней истинному высказыванию (наступления события) приписывается, ставится в соответствии символ 1 (логическая 1), а ложному (ненаступлению событий) — символ 0 (логический 0). Необходимо отметить, что символы 0 и 1никакого отношения к числовому сигналу не имеют. Они лишь описывают качественное состояние события, и поэтому к ним неприменимы арифметические операции. В электрических цепях эти символы обычно представляются также, как аналогичные в цифровом сигнале: логическая 1 — высоким, а логический 0 низким уровнем потенциала. Рассмотрим высказывание: Автомат сработает когда будут нажаты кнопки К1 и К2 или нажата кнопка К3 и не нажата кнопка К4«. Здесь простые высказывания (состояния кнопок) внедрены в сложные высказывания (срабатывания автомата) с помощью союзов — связок И, ИЛИ, НЕ; состояние кнопок играют роль аргументов (переменных), над ними эти союзы осуществляют такие функциональные преобразования, которые формируют функцию — условие срабатывания автомата.  Далее простое высказывание (событие) будем обозначать символом х, а сложное событие, являются функцией простых, — символом у.  Из изложенного ранее следует, что булева алгебра оперирует с переменными, принимающие только два значения: 0 и 1, т.е. с двоичными переменными. Функция двоичных переменных, принимающая те же два значения, называется логической функцией (переключательной функцией, функцией алгебры логики).  Логическая функция может быть выражена словесно, в алгебраической форме и таблицей, называемой переключательной таблицей или таблицей истинности.