Лінійні оператори і лінійні функціонали

Нехай є два лінійних простори і . Якщо кожному елементу x простору поставлено у відповідність цілком певний елемент y із простору , то кажуть, що заданий оператор , який діє у просторі із значеннями в .

Означення. Оператор A називається лінійним, якщо для і для будь-яких чисел α₁ і α₂ виконується рівність .

Приклад.

.

Оператор діє в просторі . Будемо вважати, що K і φ – неперервні. Перевіримо умову лінійності:

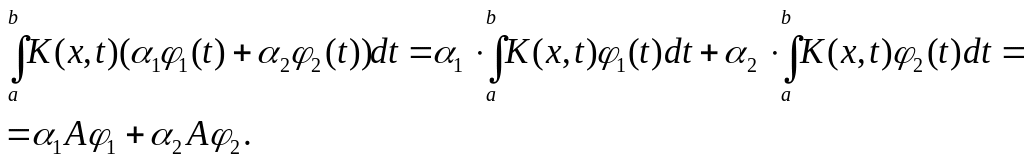
З лінійності оператора випливають властивості:

1. ;

2. .

Означення. Лінійний оператор називається неперервним в точці x₀, якщо із збіжності будь-якої послідовності випливає, що відповідна послідовність значень оператора .Тут збіжність розуміється за нормою даного простору, тобто якщо при , то .

Теорема. Якщо лінійний оператор неперервний в точці x₀, то він неперервний і в довільній точці довільного простору.

Доведення. Розглянемо довільну послідовність і покажемо, що . Розглянемо довільний елемент . Тоді в силу неперервності в x₀ . Використаємо лінійність: , тоді (при ).

Означення. Лінійний оператор, який діє в лінійному просторі із значеннями в лінійному просторі називається обмеженим, якщо існує таке число , що для .

Теорема. Для того, щоб лінійний оператор був неперервним у будь-якій точці x, необхідно і достатньо, щоб він був обмеженим.

Доведення. Необхідність. Дано: – неперервний оператор. Доведемо обмеженість, тобто що , . Припустимо протилежне, що оператор необмежений. Це означає, що для .

Розглянемо елемент і оцінимо за нормою:

, ; , , . Тоді, в силу неперервності, .

З іншого боку , не прямує до нуля, . Отримали суперечність.

Достатність. Дано, що оператор обмежений, тобто , . Доведемо, що для , .

; .

Теорему доведено.

Норма оператора.

Нехай маємо лінійний обмежений оператор: , .

Означення. Найменша з компонент , яка фігурує в умові обмеженості зветься нормою оператора A і позначається , .

По-іншому, число зветься нормою оператора, якщо для , , .

Приклад. Маємо відображення ,

.

– фіксований вектор.

– змінний вектор.

Знайдемо норму оператора

,

.

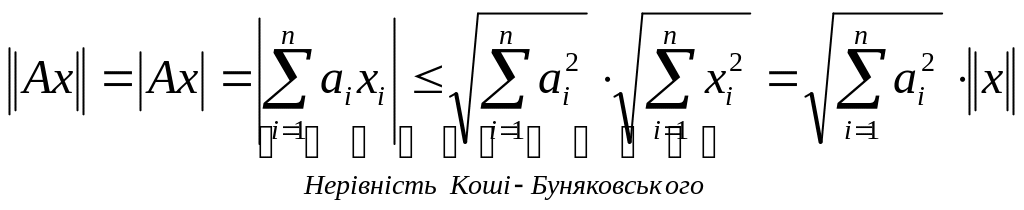Покажемо, що насправді рівна правій частині. Для цього достатньо знайти елемент x, щоб нерівність перетворювалася б в рівність. Розглянемо елемент 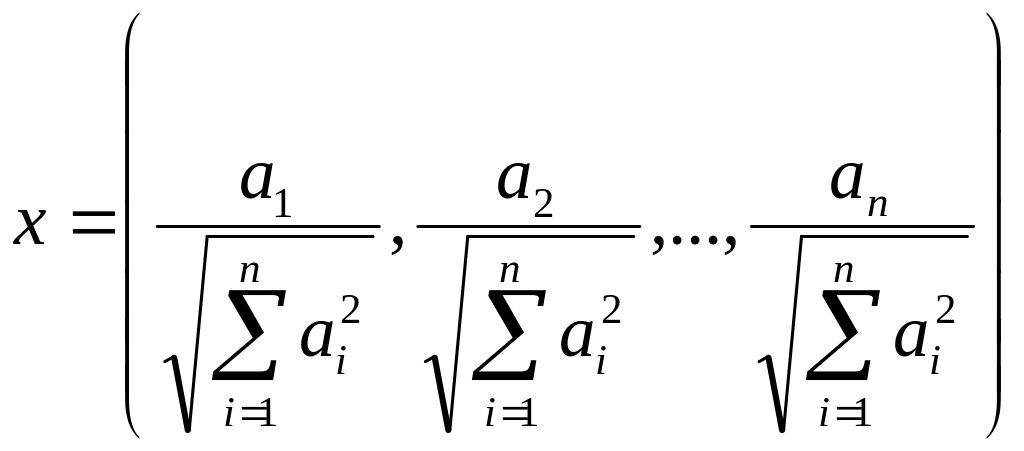, тоді:

.

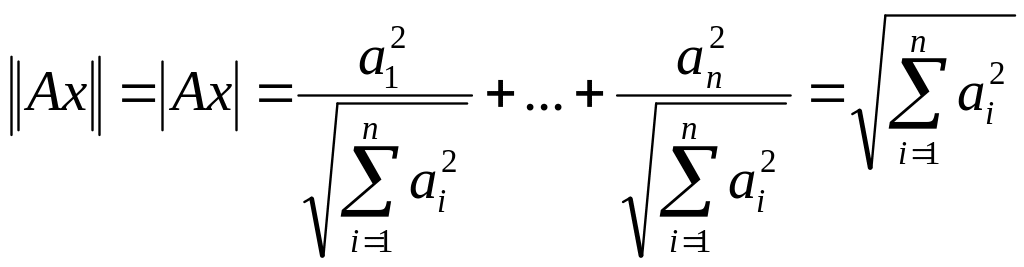Контрольні запитання.

1. Дати означення лінійного оператора.

2. Дати означення неперервності лінійного оператора.

3. Який оператор називається обмеженим?

4. Що називається нормою оператора?

5. Дати означення лінійного функціоналу. Навести приклади.

6. Який загальний вигляд лінійних функціоналів у просторах 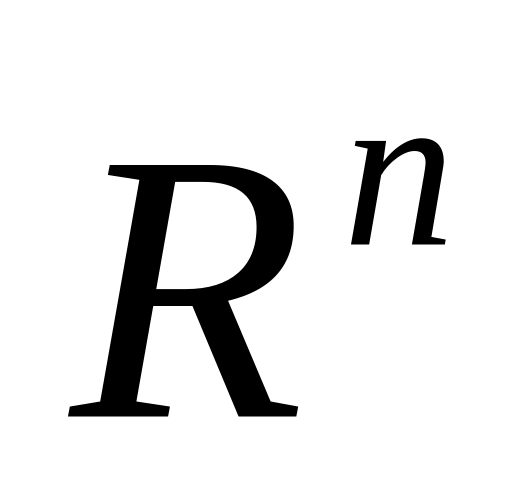і ?

7. Який оператор називається оборотним?