Конспект часть 2

Пример:

Код способный исправлять 3-х кратные ошибки при n=15, S=3

1. определяем кодовое расстояние d=2S+1=23+1=7

2. r  m(d-1) / 2 = 4(7-1) / 2 = 12

m = log2(n+1) = log2 (15+1) = 4

3. Из таблицы находим минимальные полиномы для m = 4

Таблица значений минимальных полиномов

m1(x) = 10011

m2(x) = 11111

m5(x) = 111 d-2=5

Образующий полином Р(х) определяется как произведенпие минимальных полиномов:

Р(х) = 1001111111111=10100110111=

Степень Р(х) равна 10. Уточненные числа проверочных разрядов = 10

х=n-к=15-10 =5

На основе образующего полинома строится матрица кода (15,5) сдвиг влево на (r-1), так что бы число строк было = r = 5. Образующая матрица:

первые кодовые комбинации кода БЧ

Остальные комбинации получают суммированием строк по модулю 2.(всего = 32 комбинаций образующей матрицы)

Методы инженерного проектирования системы управления. Синтез су. Методы синтеза.

Задача синтеза в том, чтобы выбрать структуру, параметрические характеристики систе6мы и технические средства реализации, так, чтобы удовлетворить совокупности заданных требований.

При проектировании из-за многоплановости и разнохарактерности сформировать единый критерий невозможно, поэтому общая задача синтеза разбивается на ряд задач:

1. определение структуры и параметров задачи;

2. формирование функциональной и принципиальной схемы;

3. выбор средств технической реализации системы;

4. конструирование аппаратуры, разработка программного обеспечения

Наиболее характерным при синтезе является задание объекта управления с исполнительными устройствами предоставляющими неизменную часть.

Выбору и расчёту подлежат усилительные , преобразующие и корректирующие устройства, составляющие изменяемую часть схемы. В ряде случаев к неизменяемым частям схемы относят усилительные и преобразующие устройства.

Заданная точность СУ обеспечивается соответствующим выбором коэффициентов передачи разомкнутой системы К>= А (заданный коэффициент передачи).

Для статистической системы стабилизации и программного управления при постоянных задающей g(t)=g0 , и возмущающих f(t), составляющих воздействие:

где Wi(0) - передаточная функция разомкнутой системы по возмущающему воздействию

Хмах - максимально допустимое значение ошибки системы без учёта ошибки чувствительного элемента.

Программная система с неединичной ОС связью или с масштабированием

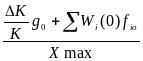, где DK возможные относительные изменения коэффициента передачи разомкнутой системы.

Астатическая система по одному или нескольким возмущающим воздействиям -

,где bi - коэффициенты пропорциональности между возмущением и скоростью изменения управляемой величины; n - число таких возмущений. m=1, 2 ... и т.д.

Следует учитывать, что полученное значение коэффициента передачи по соотношениям, в ряде случаев настолько велико, что ухудшает свойства системы.

Для обеспечения приемлемости уменьшают значение коэффициента передачи, а для достижения точности при меньших значениях К, следует повысить порядок астатизма системы на единицу по одному или нескольким возмущающим воздействиям. Последнее достигается введением в схему интегрирующего звена. но это может также привести к увеличению ошибки в системе и для уменьшения ошибки следует вводить управление по первой и второй производной ошибке системы.

При одновременном воздействии на систему полезного (задающего постоянными, медленно меняющимися возмущающими и помехами) надо решать задачу минимизации ошибок системы.

Коррекция су.

Осуществляется при помощи корректирующих устройств изменение м коэффициента передачи, постоянных времени - параметрическая оптимизация.

Для улучшения параметров качества системы - запас устойчивости.

Для коррекции структуры СУ вводится дополнительное корректирующее устройство, представляющее собой динамические звенья со специально выбранным передаточными функциями.

W(p)

Wk(p)

W(p)

+

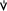
Wk(p)

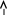
W(p)

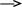
Wk(p)

Составляющие пропорциональные интеграла и производной от сигнала ошибки могут быть введены как параллельной и последовательной коррекцией. С их помощью могут реализовываться сложные законы. Составляющие пропорциональный закон чувствительности системы к помехам.

Составляющие пропорциональных интегралов повышают точность на уменьшают запас устойчивости.

Отрицательные корректирующие ОС изменяют динамические свойства системы, уменьшают влияние нелинейности звеньев, повышают стабильность коэффициента усиления при воздействии дестабилизирующих факторов.

Простейшими корректирующими устройствами являются пассивные 4-х полюсники, реализующие передаточные функции реальных дифференцирующих инерционных и интегро-диффиренциональных звеньев.

Активное корректирующее устройство реализуется на операционных усилителях. Также широко используются нелинейные корректирующие устройства и дискретные корректирующие у-ва реализованные на цифровых ЭВМ или аппаратно на линиях задержки.

Нелинейные корректирующие устройства при больших сигналах рассогласования уменьшают демпфирование системы , что расширяет её полосу пропускания и делает её более резкой.

При уменьшении сигнала рассогласования дифференцирования увеличивается , что снижает полосу пропускания, замедляет реакцию системы, уменьшая значение перегруппирования.

Предварительный выбор структуры корректирующего устройства может быть сделан на основе передаточной функции неизменяемой части системы.

Если п.ф. системы имеет вид :

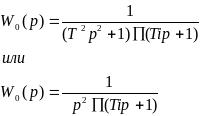
то в области частоты среза имеется отрицательный запас по фазе . для обеспечения необходимых динамических качеств такие системы надо вводить корректирующие устройства опережающие по фазе. Если неизменная часть системы содержит слабо демпферированные консервативные звенья, то могут быть использованы устройства подавляющие высокие и средние частоты, создающие отрицательный фазовый сдвиг без изменения амплитудной характеристики.

Один из самых наглядных методов построен на основе требований предъявляемых к системе по точности, запасу устойчивости и быстродействию.

Процесс синтеза по методу ЛАЧХ включает этапы:

1. построение ЛАЧХ на основе требований по точности, запасу устойчивости и быстродействию;

2. определение вида и параметров корректирующего устройства;

3. техническая реализация устройства;

4. проверочный расчёт и построение п.п.;

Использование метода Солодовникова и Бессекерского:

В основе - временные качества системы:

перегруппирование, время п.п. коэффициенты ошибок.

В основе метода Бессекерского положены частотные качества:

• ошибка при воспроизведении гармонического входного сигнала;

• показатель колебательности замкнутой системы, характеризующий её запас устойчивости.

Задача синтеза упрощается, при использовании метода стандартных коэффициентов. Сущность метода: в соответствии астатизма системы и передаточной функции её неизменяемой части с помощью значений стандартных коэффициентов выбирается приемлемый п.п. и соответствующая ему передаточная функция.

Основной недостаток - наличие большого числа варьируемых параметров.

В случаях, когда структура корректирующего устройства известна и надо выбрать некоторые параметры при известных остальных - реализуют метод квадратичных интегральных оценок.

Для систем невысокого порядка существуют готовые формулы, выражающие интегральные квадратичные оценки через коэффициенты передаточной функции.

Для выбора систем 3-го порядка используют диаграмму Виногородского с нанесёнными линиями равной степени устойчивости, затуханий и значений квадратичной интегральной оценки.