Лекция 14. Тема 8. «Плоский изгиб статически определимых стержней (балок)»

Цель лекции – рассмотреть определение перемещений сечений при деформациях изгибаемых стержней, условия жесткости изгибаемых стержней (балок), дать основные направления углубленного их изучения.

План лекции (курсивом – материалы для СРС)

1. Перемещения сечений при деформациях изгибаемых стержней.

2. Условия жесткости изгибаемых стержней.

3. Метод начальных параметров.

8.7. Перемещения сечений при деформациях изгибаемых стержней

При деформациях изгиба стержня (балки) происходят в основном два перемещения поперечных сечений:

- линейное перемещение в направлении, перпендикулярном продольной оси стержня, обычно называемое прогибом ;

- угловое перемещение (угол поворота сечения) .

Соотношение между функциями угла поворота и прогиба сечения при деформации прямого плоского изгиба стержня:

.

Приближенное выражение кривизны К (единицы измерения – 1/м) деформированной оси элемента конструкции (балки) при прямом плоском изгибе

,

где ρ – радиус кривизны деформированной оси элемента конструкции;

M_и(z) – функция от z внутренних изгибающих моментов в сечениях изгибаемого элемента конструкции (z – координата сечения, ориентированная вдоль центральной оси элемента конструкции).

Дифференциальное уравнение плоской кривой, известное из курса аналитической геометрии,

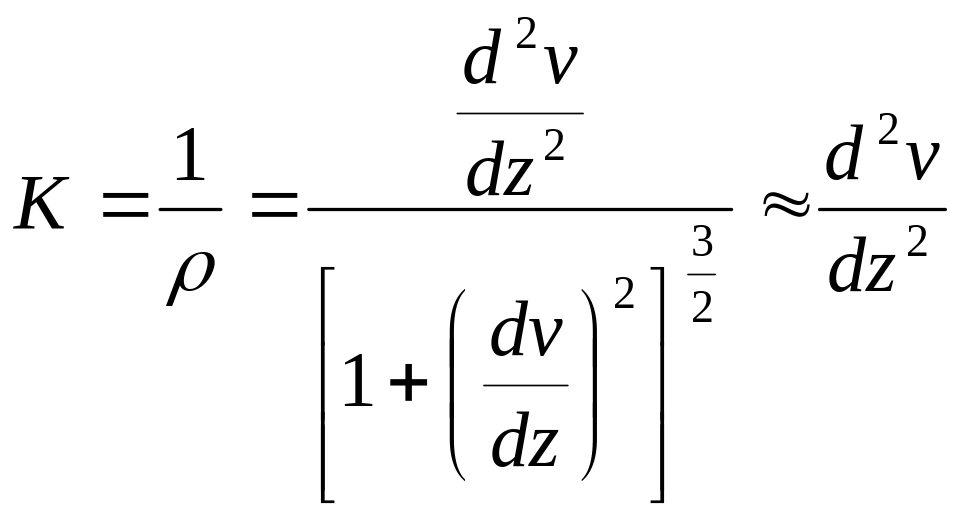
(приближенное выражение приемлемо для большинства изгибаемых элементов конструкций, например для реальных балок, у которых кривизна деформации имеет малые значения; для изгибаемых элементов с большой кривизной деформации разработана специальная теория расчета, основанная на точном выражении кривизны).

Дифференциальное уравнение деформированной центральной оси изгибаемого элемента конструкции при прямом плоском изгибе:

,

где E∙I_x – параметр жесткости изгибаемого элемента конструкции при прямом плоском изгибе (единицы измерения – Н∙м², кН∙м² и т.п.).

Интегрируя дифференциальное уравнение деформированной оси изгибаемого элемента конструкции 1-й раз, получаем выражение для угла поворота сечений

,

где – постоянная интегрирования, определяемая из начальных условий, т.е. есть угол поворота сечения, совпадающего с началом координат системы voz.

Интегрируя дифференциальное уравнение 2-й раз, получаем выражение для прогиба сечений

,

где – постоянная интегрирования, определяемая из начальных условий, т.е. есть прогиб сечения, совпадающего с началом координат системы voz.

Расчетные значения перемещений сечений при изгибе можно определить методом перемещений.

Обобщенное выражение функции внутренних изгибающих моментов в расчетном сечении стержня, записанное по методу начальных параметров:

.

Обобщенное выражение функции углов поворота расчетного сечения стержня с координатой z, применяемое для расчетов перемещений сечений по методу начальных параметров:

.

Обобщенное выражение функции прогибов расчетного сечения стержня с координатой z, применяемое для расчетов перемещений сечений по методу начальных параметров:

.

В трех вышеприведенных выражениях:

- θ_o и v_o – начальные параметры, т.е. соответственно угол поворота и прогиб сечения стержня, расположенного в начале координат О (на левом конце стержня);

- z – координата сечения, для которого рассчитываются перемещения θ_и и v (угол поворота и прогиб сечения);

- M_i, F_i, q_i – алгебраические значения внешних силовых факторов, приложенных к стержню (балке) соответственно на расстояниях a_i, b_i, c_i, n_i от начала координат o, см. обобщенную схему метода начальных параметров;

- - параметр изгибной жесткости изгибаемого стержня ( , ).