1.6. Построение кинематических диаграмм выходного звена.

Диаграмму перемещения выходного звена 5 строим в первую очередь, т.к. значения перемещения известны в 12-ти положениях механизма. По оси ординат откладываем значения перемещения с учетом масштабного коэффициента [м/мм], а по оси абсцисс откладываем время t. С учетом того, что время одного полного оборота кривошипа представлено на диаграмме отрезком длиной 180 мм, масштабный коэффициент времени

.

Диаграмму скорости выходного звена строим графическим дифференцированием диаграммы перемещения, используя метод касательных.

Задаемся полюсным отрезком интегрирования H₁ = 60 мм. Тогда масштабный коэффициент перемещения по оси ординат равен

.

Диаграмму ускорения выходного звена строим графическим дифференцированием диаграммы скорости также методом касательных.

Задаемся полюсным отрезком дифференцирования H₂ = 20 мм. Тогда масштабный коэффициент ускорения по оси ординат:

.

1.7. Силовой анализ механизма.

Целью силового анализа является определение реакций звеньев в кинематических парах механизма, а также уравновешивающего момента, который уравновешивает систему заданных активных сил и сил инерций. Для силового расчета механизма будем использовать метод кинетостатики.

Рассмотрим расчетное (2-е) положение механизма.

Определяем активные силы, действующие на звенья механизма.

На звенья 1, 3 и 5 действуют силы тяжести, приложенные в соответствующих центрах тяжести звеньев:

На выходное звено 5 на рабочем ходу действует сила полезного сопротивления , значение которой изменяется в соответствии с заданной диаграммой нагрузки, а на холостом ходу – постоянная сила сопротивления = 710 [Н]. Расчетное (2-е) положение механизма соответствует рабочему ходу, поэтому, согласно диаграмме, принимаем [Н].

Определим инерционную нагрузку, действующую на звенья механизма. Совокупность сил инерции, действующих на каждое отдельное звено, приводим к главному вектору и главному моменту сил инерции этого звена.

Сначала рассчитаем главные векторы сил инерции звеньев:

, т.к. центр тяжести S₁ неподвижен;

[Н]; [Н].

Главные векторы сил инерции направлены противоположно векторам ускорений центров тяжести соответствующих звеньев.

Рассчитаем главные моменты сил инерции звеньев:

;

[Н·м].

Главные моменты сил инерции направлены противоположно угловым ускорениям соответствующих звеньев.

Согласно принципу Даламбера, заданный рычажный механизм можно формально рассматривать находящимся в состоянии равновесия под действием приложенных активных сил, инерционных сил, и уравновешивающего момента M_ур, который, по сути, является реактивным моментом, действующим на вал входного звена 1 со стороны выходного вала редуктора.

Разделим механизм на группы Ассура и входное звено, заменив отброшенные связи (т.е. звенья) реакциями, и поочередно рассмотрим их равновесие.

Для удобства и наглядности решения задачи изображаем на чертежном листе группы Ассура и входное звено с масштабным коэффициентом и показываем направления всех сил, приложенных к звеньям.

Сначала рассмотрим группу Ассура 4–5. Составляем векторное уравнение равновесия системы сил, действующих на звенья группы:

Рассмотрим отдельно звено 4 (рис. 2).

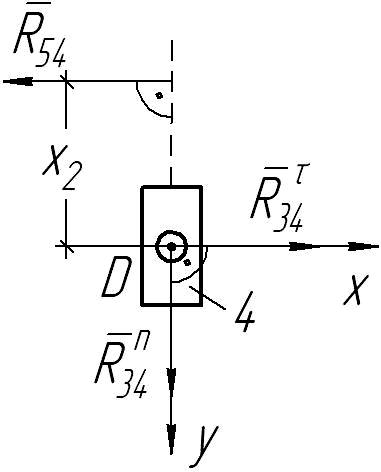
Рис. 2. Схема нагружения кулисного камня 4

Вводим вспомогательную локальную систему координат xDy и составляем три уравнения равновесия звена 4:

Из первого уравнения следует, что . Из третьего уравнения следует, что x₂ = 0, следовательно, вектор реакции проходит через точку D.

Строим план сил группы Ассура 4–5 согласно векторному уравнению. Принимаем масштабный коэффициент .

Рассчитываем длины отрезков, изображающих векторы сил на плане сил:

[мм]; [мм];

[мм].

Решение уравнения на плане сил получаем, проводя линии действия неизвестных реакций и до их пересечения. Реакцию во внутренней кинематической паре группы найдем из условия равновесия звена 5:

Т.к. в этом уравнении известны все силы, кроме искомой реакции , то её вектор можно построить замыканием четырех известных векторов сил на плане сил.

После построения плана сил из него можно найти:

[Н];

[Н]; [Н].

Для определения координаты точки приложения равнодействующей реакции составим уравнение равновесия звена 5 в виде:

;

[м].

Знак «–» означает, что равнодействующая приложена слева от точки S₅.

Рассматриваем следующую группу Ассура 2–3.

Составляем векторное уравнение равновесия группы:

Рассмотрим отдельно звено 2 (рис. 3).

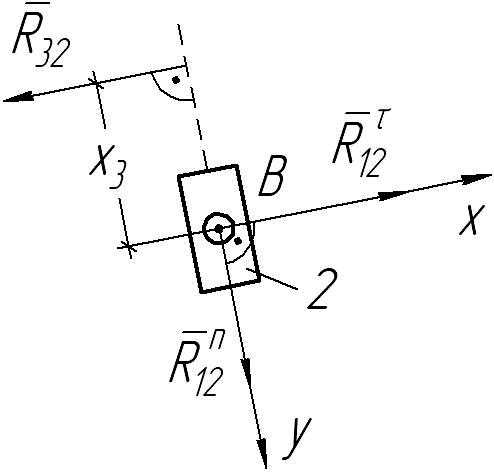
Рис. 3. Схема нагружения кулисного камня 2

Вводим вспомогательную локальную систему координат xBy и составляем три уравнения равновесия звена 2:

Из первого уравнения следует, что . Из третьего уравнения следует, что x₃ = 0, следовательно, вектор реакции проходит через точку B.

Величину реакции можно определить, составив уравнение равновесия группы в целом:

;

Строим план сил группы Ассура 2–3 согласно векторному уравнению. Принимаем масштабный коэффициент [Н/мм].

Рассчитываем длины отрезков, изображающих векторы сил на плане сил:

[мм]; [мм];

[мм]; [мм].

Т.к. в этом уравнении известны все силы, кроме искомой реакции , то её можно построить простым замыканием многоугольника сил. Реакцию во внутренней кинематической паре группы найдем из условия равновесия звена 3:

Вектор строим замыканием векторов остальных сил на плане сил.

После построения плана сил из него находим:

[Н]; [Н].

Рассмотрим равновесие входного звена механизма.

Запишем векторное уравнение равновесия:

Строим план сил входного звена 1 согласно векторному уравнению. Принимаем масштабный коэффициент .

Длины отрезков, изображающих векторы сил на плане сил:

[мм]; [мм].

В уравнении равновесия известны все силы, кроме , поэтому её можно легко построить замыканием многоугольника сил.

После построения плана сил из него находим:

[Н].

Для определения величины уравновешивающего момента запишем уравнение равновесия моментов входного звена в виде:

;

[Н·м].