5.9. Арифметические вычисления
Язык Пролог не предназначен для программирования задач с большим количеством арифметических операций. Для этого используются процедурные языки программирования. Однако в любую Пролог-систему включаются обычные арифметические операции и функции:
X + Y |
Сумма X и Y |
X - Y |
Разность X и Y |
X * Y |
Произведение X и Y |
X / Y |
Деление X на Y |
X mod Y |
Остаток от деления X на Y |
abs(X) |
Абсолютная величина числа X |
sqrt(X) |
Квадратный корень из X |
random(X) |
Случайное число в диапазоне от 0 до 1 |
random(Int,X) |
Случайное целое число в диапазоне от 0 до Int |
sin(X) |
Синус X |
cos(X) |
Косинус X |
tan(X) |
Тангенс X |
log(X) |
Натуральный логарифм (ln) числа X |
Пролог располагает двумя числовыми типами доменов: целыми и действительными числами. Пролог позволяет также сравнивать арифметические выражения, используя отношения:
=, <, <=, >, >=, <>
Для реализации математических действий в Прологе используются предикаты. Следующие примеры демонстрируют их использование.
Пример 1.
Найти среднее арифметическое двух чисел.
PREDICATES
Sr (real, real, real)
CLAUSES
Sr (A, B, S):- S = (A+B)/2.
GOAL
Sr (8, 12, S), write (S).
Результат:
10
Пример 2.
Определить является ли натуральное число четным или нечетным
PREDICATES
Chet (integer)
CLAUSES
Chet (A): - A mod 2 =0, write (A, ‘- четное’); Write (A, ‘- не четное’).
GOAL
Chet (18).
Результат:
18 – четное
5.10. Рекурсия
Рекурсия – это второе средство для организации повторяющихся действий в ПРОЛОГе. Рекурсивная процедура – это процедура, вызывающая сама себя до тех пор, пока не будет соблюдено некоторое условие, которое остановит рекурсию. Такое условие называют граничным. Рекурсия – хороший способ для решения задач, содержащих в себе подзадачу такого же типа. Рекурсивное правило всегда состоит по крайней мере из двух частей, одна из которых является не рекурсивной. Она определяет граничное условие.
Рассмотрим рекурсивное определение правила на примере правила predok
1. X является предком Z, если X - родитель Z
predok(X, Z):-roditel(X, Z)
2. X – предок для Z, если найдется такой Y, для которого X является родителем и Y является предком Z .
Predok (X,Z) :- roditel (X,Y), predok (Y,Z).
Первая часть этого правила нерекурсивная, она определяет условие завершения рекурсии. Поиск прекратится, как только будет найден ближайший предок - родитель.
Программа:
DOMAINS
name = string
PREDICATES
roditel (name, name)
predok (name, name)
CLAUSES
roditel (коля, оля).
roditel (оля, маша).
predok (X, Z):- roditel (X, Z).
predok (X, Z):- roditel (X,Y), predok (Y, Z).
GOAL
predok (коля, маша).
Результат:
yes
Пример. Рекурсивное вычисление факториала
Задача нахождения значения факториала n! сводится к нахождению значения факториала (n-1)! и умножения найденного значения на n.
Правило для вычисления факториала:
1. 0! = 1
fact (0, 1):- !. % нерекурсивная часть правила
2. N! = (N-1)!*N.
fact (N, FN):- M=N–1, % рекурсивная часть правила
fact (M, FM), FN=FM*N.
Программа:
PREDICATES
fact (integer, integer)
CLAUSES
fact (0, 1):- !.
fact (N, FactN):- M=N–1, fact (M, FactM), FactN=FactM*N.
GOAL
fact (3, FN), write (“3!=”, FN).
Результат работы программы:
3!=6
Для наглядного представления нахождения решения удобно использовать дерево целей:
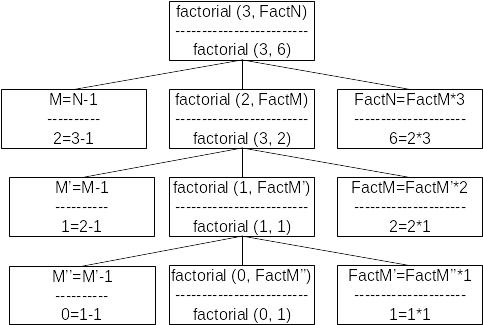
рис.3 Целевое дерево вычисления факториала