Тема № 6 Оценка параметров трехфазных цепей с различными нагрузками

Цель занятия: Анализ и оценка рабочих параметров трехфазной цепи с активной и реактивной нагрузкой, соединенной по схеме звезда или треугольник.

Данная работа показывает особенности оценки параметров трехфазных цепей с нагрузкой, соединенной по схеме звезда или треугольник, а также с принципы построения векторных диаграмм для симметричной и несимметричной, активной и пассивной нагрузки. Для пояснения методики решения задач по трехфазным цепям приведены примеры с решениями и построе­нием векторных диаграмм.

На рисунке 6 приведен пример трехфазной цепи, содержащей трехфазный генератор и трехфазную нагрузку, соединенную по схеме звезда [4].

П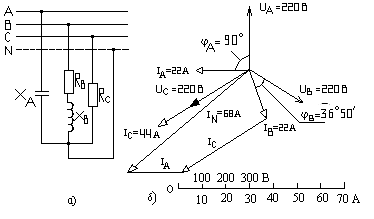 ример 6.1. В 4-х проводную трехфазную сеть (рис. 6.1) с линейным напряжением U_Л = 380B включена звездой несимметричная нагрузка: в фазе А - конденсатор с со­противлением х_С(A)=10 Ом; в фазе В - катушка индуктивности с сопротивление R_L(B) = 8 Ом и х_L(C) = 6 Ом, в фазе С - активное сопротивление R_(C) = 5 Ом.

Д ля схемы (рис. 6.1.а) определить фазные токи, начертить в масштабе векторную диаграмму цепи и найти ток в нулевом проводе.

Решение:

1) U_A =U_B =U_C = U_Л /√3 =

380/1,73 = 220 (B).

Рис. 6.1. Четырехпроводная трехфазная цепь

Рис. 6.1.

2. Полное сопротивление в каждой фазе:

Z _А = х_С(A)=10 e^–j90˚(Ом); Z_В = R_В²+X_В²·e ^{j arctg (x/r)} = 10·e^{j 36}˚⁵⁰; Z_А = R_(C) = 5e^j0˚ (Ом).

3. Находим фазовые токи: I_A = U_A/x_A = 220·e ^j0˚/10·e ^j-90˚ = 22·e^+j90˚(A);

I_B = U_B/Z_В = 220·e^–j120˚/10·e ^j36˚⁵⁰ = 22·e^–j156˚⁵⁰ (A);

I_C = U_C/R_C = 220·e ^j120˚/5·e ^j0˚ = 44·e ^j120˚ (A).

Вектор тока I_A опережает вектор напряжения U_A на угол φ= 90˚(свойство С эл-та).

Вектор тока I_B отстает от вектора напряжения U_В на угол φ_B (свойства L эл-та), который определяется из выражения: cos φ_B = R_B/Z_В = 8/10 = 0,8. φ_B = 36˚50’.

Ток I_С совпадает с вектором напряжения U_C. Ток в нулевом проводе в масштабе построения равен гео­метрической сумме трех фазных токов, например, I_N = 66 A.

Ī _N = Ī_A + Ī_B + Ī_C.

Ī_N = (I_A·cos⁹⁰ +jI_A·sin⁹⁰)+(I_B·cos^–156˚⁵⁰ + jI_B·sin^–156˚⁵⁰)+(I_C·cos¹²⁰˚ + jI_C·sin¹²⁰˚);

Ī_N = + j22 + [22·(–0,92) + j22·(–0,40)] + [44·(–0,5) + j44·(0,866)];

Ī_N = j22 + (–20,24–j8,8) + (–22 +j38,1) = (–42,24–j51,3) (А);

I _N = (–42,24)² + (–j51,3)² ·exp ^{j arctg (-x/-r)} = 66,45·exp ^j+50˚³⁰ (А).

Далее определяем мощности ∑Р; ∑Q; ∑S потребляемые нагрузками.

Мощность S = U∙I’ в 3-х фазной цепи находят по сопряженному току Iʹ.

Активная мощность составит: P = P_B + P_C = Iʹ_B²∙R_B + Iʹ_C²∙R_C (Вт).

Реактивная мощность составит: Q = Q_В + (-jQ_А) = Iʹ_В²∙Х_В + Iʹ_A²∙(-jХ_A).

П

Рис. 6.2.

ример 6.2. В трехфазную сеть с U_Лин = 220 B включена треугольником несимметричная нагрузка (рис. 6.2,а): в фазе АВ – конденсатор (х_АВ=10 Ом); в фазе ВС - катушка с (R_ВС = 4 Ом и х_ВС = 3 Ом); в фазе СА - активное сопротивл. (r_СА = 10 Ом).

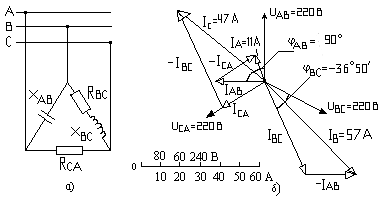
Рис. 6.2. Трехпроводная схема соединения треугольником

Определить фазные токи, углы сдвига фаз и начертить в масштабе векторную диаграмму цепи, по которой определить числовые значения линейных токов.

Решение. Определим фазные токи и углы сдвига фаз:

I_AB = U_АВ/x_AB = 220·e ^j0˚/10·e ^j–90˚ = 22·e ^j90˚ = j22 (A); (ток в С эл-те опережает);

I_BС = U_ВС/Z_BC = 220·e ^j-120˚/5·e ^j36˚⁵⁰ = 44·e ^j–156˚⁵⁰ = (– 40,35 – j17,54) (A);

I_СA = U_СA/R_CA = 220·e ^j120˚/10·e ^j0˚ = 22·e ^j120˚ = (–11 + j19,05) (A);

Ī_A = Ī_AB – (Ī_CA) = j22–(–11+j19,05) = j22+11–j19,05 = (11+j3) = 11,4·exp ^j15,15˚ (А);

Ī_B = Ī_BC – (Ī_AB) = (–40,35–j17,54)–j22 = (– 40,35– j39,54) = 57,06·e ^j44˚⁴⁰ (А);

Ī_C = Ī_CA – (Ī_BC) = (–11+j19,05)–(–40,35–j17,54) = (29,35+j36,59) = 46,9·e ^j51˚²⁶ (А).

Проверка: ∑(Ī_A+Ī_В+Ī_С) = 0 = (11+j3)+(–40,35–j39,54)+ (29,35+j36,59) = 0.

Далее определяем мощности, потребляемые нагрузками: ∑Р; ∑Q; ∑S.

Мощность в 3-х фазной цепи S = U∙Iʹ находят используя сопряженный ток Iʹ.

Активная мощность составит: P = P_BC + P_CA = Iʹ_BC²∙R_BC + Iʹ_CA²∙R_CA (Вт).

Реактивная мощность составит: Q = Q_ВС + (-jQ_АВ) = Iʹ_ВС²∙Х_ВС + Iʹ_СА²∙(-jХ_AB).

Пример 6.3. В трехфазную 4-х проводную сеть (рис. 6.3) с линейным напряжением U_Лин = 380B включена печь (симметричная нагрузка с сопротивлением R, соединенная треугольником), а также включены лампы накаливания (несимметричная нагрузка – звезда). Мощность каждой фазы печи P_П = 10000 Вт. Мощность каждой лампы Р_Л = 200 Вт, число ламп в фазах: n_A = 50; n_B = 40; n_C = 30.

О

Рис. 6.4.

пределить показания приборов, включенных в схему – рис. 6.3.

Решение. Находим фазные токи, потребляемые печью:

I_AB = I_BC = I_CA = P_П/U_ном = 10∙1000/380 = 26,3 (А).

2 . Линейные токи, потреб-ляемые симметричной наг-рузкой нагревателей печи:

I _A=I_B=I_C= 3∙26,3 = 45,5 (А).

3. Определим фазные токи, потребляемые лампами.

Лампы сое­динены по схеме звезда и включены на фазные напряжения:

Рис. 6.3. Трехфазная цепь для примера №6.3

U_А = U_B = U_С = U_Ном /√3 = 220 (В).

Фазные токи составят: I_A = Р_Л∙n_A/U_А = 200∙50/220 = 45,4 (A).

I_В = Р_Л∙n_В/U_В = 200∙40/220 = 36,4 A. I_С = Р_Л∙n_С/U_С = 200∙30/220 = 27,3 (A).

Ī_N = (45,4)+[36,4·(–0,5)+j36,4·(–0,866)]+[27,3·(–0,5) +j27,3·(0,866)]= (13,55–j7,87),

I _N = 13,55²+(-7,87²)·exp ^{j arctg (х/r)} = 15,67·exp ^j–30˚(А).

4 . Активная мощность в любой фазе составит: Р_i = U_Ф.i ·Iʹ_Ф.i = (U_Л.i ·I_{Л. i})/ 3 .

Определяем суммарную мощность, потребляемую нагрузками.

Строим векторы линейных и фазных токов.

Пример 6.4. Требуется определить линейные токи в нагрузке, соединенной тре­угольником, которая подключена к симметричному трехфазному генератору с линейным напряжением E_Л = 220 В. Сопротивления фаз приемника имеют значе­ния: Z_AB = Z_BC = 50 Ом, Z_CA = (30 + j40) Ом.

Схема соединений источника с нагрузкой приведена на рис. 6.4, а.

Решение. Приемник - схема с неравномер­ной нагрузкой фаз генератора.

Вначале определяем фазные токи (они имеют двухиндексные обозначения):

Ī_AB = Ū_AB/Ż_AB = 220/50 = 4,4 (A).

Ī_BC =Ū_BC/Ż_BC = 220·e^–j120˚/50 = 4,4·e^–j120˚= 4,4·(–0,5)+j4,4·(–0,866)= –2,2–j3,81;

Ī_CA =Ū_CA/Ż_CA = 220·e^j120˚/50 = 4,4·e^j120˚ = 4,4·(–0,5)+j4,4·(+0,866) = –2,2+j3,81.

Затем определяем линейные токи (они обозначаются одноиндексно):

Ī_A = Ī_AB – (Ī_CA) = (4,4) – (–2,2 +j3,81) = (6,6 –j3,81) = 7,62·e^–j30˚ (А);

Ī_B = Ī_BC – (Ī_AB) = (–2,2 –j3,81) – (4,4) = (–6,6 –j3,81) = 7,62·e^j210˚ (А);

Ī_C = Ī_CA – (Ī_BC) = (–2,2 +j3,81) – (–2,2–j3,81) = +j7,62 = 7,62·e^j90˚ (А).

Рис. 6.4. Схема трехфазной цепи (а) и ее векторная диаграмма (б)

Сумма линейных токов в цепи составит:

Ī_A + Ī_B + Ī_C = (6,6 –j3,81)+(–6,6 –j3,81)+(j7,62) = 0 (условие проверки).

П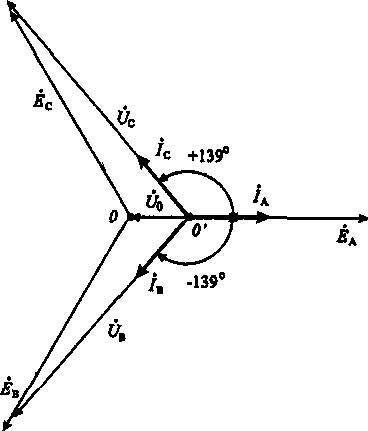 ример 6.5. Требуется определить токи в фазах приемника, соединенного звездой без нулевого провода, если сопротивления нагрузок имеют значения z_a = 5 Ом Z_В = Z_С = 10 Ом, фазное напряжение генератора Е = 100 В.

Построить векторную диаграмму для токов в цепи.

Решение. Определим нулевое напряжение. Поскольку два сопротивления нагрузки имеют одно и то же значение Z_В = Z_С, то основную формулу (а)

Ū_Nn = (Ē_AY_A + Ē_BY_B + Ē_CY_C)/(Y_A+Y_B+Y_C+Y₀), (а)

можно упростить.

Учитывая, что a^–1= e^–j120° = (–1–j3/2), из форму-лы (а) получим формулу (b):

Ū_Nn=Ē_A(Y_B–Y_A)/(Y_B+2Y_A)=100(10–5)/(10+10)= 25V.

Рис. 6.5. Векторная диаграмма напряжений и токов.

Найдем напряжения на фазах приемника: Ū_А = (Ē_A – Ū₀) = 100 – 25 = 75 (В);

Ū_В = (Ē_В–Ū₀) = 100a^–1–25 = [100(–0,5)+j100(–0,866)]-25 = (–75–j86) = 115·e^–j139˚(B);

Ū_C = (Ē_C–Ū₀) = 100a–25 = [100(–0,5)+j100(0,866)]-25 = (–75+j86) = 115·e^j139˚ (B).

Определим токи в фазах приемника: Ī_A = (Ū_A /Ź_A) = 75/5 = 15 (A);

Ī_B =(Ū_B /Ź_B)=(115·e^–j139˚)/10=(11,5·e^–j139˚); Ī_C =(Ū_C /Ź_C)=(115·e^j139˚)/10=(11,5·e^j139˚).

Пример 6.6. Обратная задача. По векторной диаграмме для трехфазной цепи (рис. 6.6), с нагрузкой, включенной по схеме звезда, определить характер нагрузки каждой фазы и вычислить ее сопротивление, а также начертить схему цепи. Определить мощность Р, Q, S. Векторы линейных напряжений на схеме не показаны.

Решение. На векторной диаграмме видно, что ток в фазе А отстает от фазного напряжения U_А на угол φ_А = –5 3˚10ʹ. Следовательно, в фазу А включена катушка с полным сопротивлением Z_A = u_A / i_A = 220/22 = 10 Ом.

Для цепи (рис. 6.7) определим активное и индуктивное сопротивление:

R_A = Z_A∙cos′ φ_А = 10cos′ (+53˚10΄) = 10∙0,6 = 6 (Ом); (cos′ – сопряж. угол).

x_A = jZ_A∙sin′ φ_А = j10sin′ (+53˚10΄) = j10∙0,8 = j8 (Ом).

В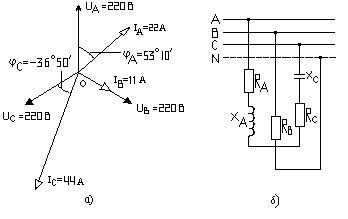 фазе В ток I_B совпадает с напряжением U_B значит в фазу В включено активное сопротивление

R_B = U_B/I_B = 220/11 = 20 (Ом).

В фазе С ток I_С опережает напряж. U_С на угол φ_С = 36˚50' (вращение вектора по час. стрелке); значит в фазу С включены конденсатор и активное сопротивление.

Рис. 6.6. Обратная задача cos′, sin′ – сопряженный угол.

Полное сопротивление фазы С составит:

Z_C = U_C/I_C = 220/44 = 5 (Ом); R_С = Z_Сcosʹφ_С = 5 cosʹ(–36˚50΄) = 5∙0,8 = 4 (Ом);

x_С = Z_Сsin φ_С = 5 sinʹ(–36˚50΄)= –5∙0,6 = –3 (Ом).

2. Определяем мощности, потребляемые цепью. Активная мощность составит:

P = P_A+P_B+P_C = I_A²∙R_A + I_B²∙R_B + I_C²∙R_C = 22²∙6+11²∙20+44²∙4 = 13 065 (Вт).

Реактивная мощность составит:

Q = Q_A + Q_C = I_A²∙Х_L + I_С²∙Х_С = 22²∙j8 +(44²∙–j3) = –j1936 ВАР = –1,93 (кВАр).

П

Рис. 6.7.

ример 6.7. Сравним значение тока в нулевом проводе и положение его вектора при переста- новке элементов фазных нагрузок, включенных по схеме звезда.

Определим параметры цепи для схемы на рис. 6.7 (a,b,c,d).

Д ано: U_Ф =10В; R =10; X_L =j10; X_C = –j10;

I_A = U_A/R_A = 10·e ^j0˚/10·e ^j0˚ = 1 (A).

I_B = U_B/X_C = 10·e^–j120˚/10·e^–j90˚ = 1·e^–j30˚ (A).

I_C = U_C/X_L = 10·e ^j120˚/10·e ^j90˚ = 1·e ^j30˚ (A).

I _N = I_A+I_B+I_C =1+(0,866–j0,5)+(0,866+j0,5)=2,73.

Поменяв местами элементы цепи увидим, что вектор тока I_N поветнется на φ =120^о.

Дано: U_Ф =10В; R =10; X_L =j10; X_C = –j10;

I_A = U_A/X_L = 10·e ^j0˚/10·e ^j90˚ = 1·e^–j90˚ (A).

I_B = U_B/X_C = 10·e^–j120˚/10·e^j0˚ = 1·e^–j120˚ (A).

I_C = U_C/X_C = 10·e ^j120˚/10·e^–j90˚ = 1·e ^j210˚ (A).

I_N = I_A + I_B + I_C = -j1+ (-0,5-j0,866) + (-0,866-j0,5) = – 1,366 –j2,366 = 2,73·e ^j60˚ (A).

Если вновь переместить элементы R,L,C, то вектор тока I_N вновь повернется на φ =120 ^о.

РГР № 6.1. Задание для самостоятельного решения

1. Выполнить расчет параметров трехфазной цепи с нагрузкой (рис. 6.2 и 6.3).

2. Показать векторные диаграммы токов и напряжений.

Варианты и параметры элементов (для рис. 6.2 и 6.3) приведены в таблице №6.1

Т аблица 6.1. Параметры для индивидуального задания по теме трехфазные цепи

№	схема вкл. нагрузки	UЛ – (В)	ω рад/с	RА (Ом)	ХА.L (Ом)	ХА.C (Ом)	RВ (Ом)	ХВ.L (Ом)	ХВ.C (Ом)	RС (Ом)	ХС.L (Ом)	ХС.С (Ом)	∑Р (BТ)	∑Q (BAР)	∑S (BA)
1	Звезда.	110	250	80	-	60	100	–	25	80	50	–
2	Треугольник	110	250	100	50	-	30	150	80	100	-	50
3	Звезда.	220	314	150	200	-	300	100	-	40	210	100
4	Треугольник	220	314	40	40	140	300	60	-	200	30	-
5	Звезда.	330	380	200	-	35	20	100	30	100	-	80
6	Треугольник	330	380	250	100	-	200	-	60	20	200	80
7	Звезда.	380	500	150	250	-	330	-	200	300	-	80
8	Треугольник	380	500	330	-	55	330	100	-	50	120	300
9	Звезда.	440	628	100	200	-	220	-	150	40	100	40
10	Треугольник	440	628	90	-	30	100	-	50	110	30	-
11	Звезда.	110	250	60	-	220	100	300	-	60	-	80
12	Треугольник	110	250	55	100	-	75	-	600	100	100	-
13	Звезда.	220	314	10	200	50	85	-	50	30	40	200
14	Треугольник	220	314	120	-	60	50	30	130	200	-	60
15	Звезда.	330	380	160	-	350	140	60	-	180	50	-
16	Треугольник	330	380	40	220	100	50	-	250	50	33	-
17	Звезда.	380	500	100	-	300	100	150	-	100	-	50
18	Треугольник	380	500	70	350	-	50	200	50	100	220
19	Звезда.	440	628	220	-	55	140	-	100	70	-	44
20	Треугольник	440	628	25	160	50	40	-	80	50	130	-
21	Звезда.	110	250	300	100	-	200	150	-	50	-	150
22	Треугольник	110	250	180	-	110	70	190	100	100	-	200
23	Звезда.	220	314	300	-	50	600	-	75	40	50	280
24	Треугольник	220	314	250	80	-	50	260	60	220	-	44
25	Звезда.	330	380	300	-	55	300	-	200	60	140	66
26	Треугольник	330	380	40	175	75	200	45	-	200	100	-
27	Звезда.	380	500	300	66	-	400	-	200	100	44	44
28	Треугольник	380	500	70	180	80	200	30	-	200	-	55
29	Звезда.	440	628	300	-	100	20	80	180	55	140	60
30	Треугольник	440	628	200	100	-	100	-	380	230	-	80

Значения тригонометрических функций приведены в приложении П2.

КГР № 6.2. Задание для контрольно-графической работы

1. Определить параметры трехфазной цепи: I_Л; I_Ф; P, Q, S, (U_Nn, I_N).

2. Показать векторные диаграммы токов и напряжений.

3. Варианты и № схем - стр. 44; величины параметров элементов – в табл. №6.2.

Т аблица 6.2. Параметры для индивидуального задания по теме трехфазные цепи

№	№ схемы (рисунка)	Е (В)	I	f Гц	ω рад/с	Z1А, (АB) (Ом)	Z1B, (ВC) (Ом)	Z 1C, (СА) (Ом)	Z2A, (АB) (Ом)	Z2В, (ВC) (Ом)	Z2C, (СA) (Ом)
1	рис. № 6.9	40		150		40	20–j40	60+j60	10–j40	j10	20–j30
2	рис. № 6.10	60		125		10+j60	j60	30+j30	20–j20	45–j45	30
3	рис. № 6.11	80		100		40-j20	20+j60	80	j40	80-j80	10-j40
4	рис. № 6.12	100		75		j50	20+j40	40-j50	50+j50	60	80-j25
5	рис. № 6.9	120		50		120+j60	60	30-j40	40-j40	30-j60	-j30
6	рис. № 6.10	140		25		250	100	-j70	70	70+j70	140+l4
7	рис. № 6.11	50		150		25-j50	50+j25	-j10	5-j10	j25	20-j100
8	рис. № 6.12	70		125		j35	35+j35	35-j7	17,5-j7	35+j70	35
9	рис. № 6.9	90		100		30+j45	90	9-j9	30	22,5-j9	45+j45
10	рис. № 6.10	200		75		100+j40	50	50-j40	-j100	100+j20	50+j50
11	рис. № 6.11	160		50		40-j80	16+j32	-j20	100+j100	40	20-j40
12	рис. № 6.12	180		25		45+j22,5	j45	90-j45	90-j18	18+j36	j60
13	рис. № 6.9	20		50		10+j15	4-j5	5+j4	5-j7	15+j3	-j10
14	рис. № 6.10	40		75		-j10	10+j4	40+j20	20-j5	30+j20	20-j30
15	рис. № 6.11	60		100		15+j10	20-j3	30	15-j20	j20	6+j6
16	рис. № 6.12	80		125		10-j20	10+j40	8-j16	40+j10	25-j10	20
17	рис. № 6.9	40		150		40	20–j40	60+j60	10–j40	j10	20–j30
18	рис. № 6.10	60		125		10+j60	j60	30+j30	20–j20	45–j45	30
19	рис. № 6.11	80		100		40-j20	20+j60	80	j40	80-j80	10-j40
20	рис. № 6.12	100		75		j50	20+j40	40-j50	50+j50	60	80-j25
21	рис. № 6.9	120		50		120+j60	60	30-j40	40-j40	30-j60	-j30
22	рис. № 6.10	140		25		250	100	-j70	70	70+j70	140+l4
23	рис. № 6.11	50		150		25-j50	50+j25	-j10	5-j10	j25	20-j100
24	рис. № 6.12,	70		125		j35	35+j35	35-j7	17,5-j7	35+j70	35
25	рис. №6.9	90		100		30+j45	90	9-j9	30	22,5-j9	45+j45
26	рис. № 6.10	200		75		100+j40	50	50-j40	-j100	100+j20	50+j50
27	рис. № 6.11	160		50		40-j80	16+j32	-j20	100+j100	40	20-j40
28	рис. № 6.12	180		25		45+j22,5	j45	90-j45	90-j18	18+j36	j60

Рекомендуемая литература

1. Касаткин А.С., Немцов М.В. Электротехника. – М.: Высш. шк., 2003. – 540 с.

2. Рекус Г.Г. Основы электротехники и промышленной электроники в примерах

и задачах с решениями: Учебное пособие. – М.: Высш. шк., 2008. – 343 с.

3. Сборник задач по электротехнике и основам электроники / Под ред. В.Г. Герасимова. – М.: Высш. шк., 1987. – 288 с.

4. Березкина Т.Ф., Гусев Н.Г. Задачник по общей электротехнике с основами электроники. – М.: Высш. шк., 1983. – 368 с.