Тема №1 Методы преобразования цепей и элементов и определение их эквивалента

Цель занятия: приобретение умений и навыкок соединения элементов в схемах (последовательное, параллельное и смешанное) и методов преобразования схем, с целью их упрощения и определения эквивалентного параметра исходной схемы.

Методы преобразования используют для снижения количества элементов.

Они основаны на упрощении некоторой модели электрической цепи, с целью получения эквивалентной схемы, параметры которой аналогичны исходной.

Определение параметров эквивалентных элементов связано с требованиями сохранения равенства токов, как в исходной, так и в преобразованной цепи.

Для упрощения сложной цепи выбирают узел или контур, например, преобразуют схему звезда в схему треугольник или наоборот; затем для упрощенной схемы выполняют расчет, определяя эквивалентный параметр исходной схемы.

1.1. Методы преобразования сложной цепи и определение её эквивалента

П ример 1.1. Для цепи (рис.1.1) требуется определить полное сопротивление R_ЭКВ.СД, и ток I_И

преобразовав цепь из треугольника АВС (R₂, R₅, R₆) в цепь звезды (R₂₅, R₂₆, R₅₆).

R₂ = R₃ = R₄ = R₅ = R₆ = 10(Ом).

R₂₅ = (R₂+R₅)+[(R₂·R₅)/R₆] = 30;

R₂₆ = (R₂+R₆)+[(R₂·R₆)/R₅] =30;

R₅₆ = (R₅+R₆)+[(R₅·R₆)/R₂] = 30. При Е = 5,1 В, I_И = Е/R_ЭКВ.СД = 0,1 А.

R_ЭКВ.СД = R₂₅ + [(R₅₆+R₄)(R₂₆+R₃)] / [(R₅₆+R₄+R₂₆+R₃)] = 30+20 = 50 (Ом).

Пример 1.2. Требуется определить полное Z сопротивление для цепи (рис.1.2).

Дано: R₁ = 6; R₂ = 1; R₃ = 5; R₄ = 2; R₅ = 4; R₆ = 8; (Ом).

Решение. Варианты преобразования исходной схемы показаны на рис. 1.2 б, в, г.

1) Вначале найдем значения резисторов при преобразовании их в схеме звезда.

Если преоразовать соединенные звездой резисторы R₄, R₅, R₆ в эквивалентное

соединение треугольником резисторов r₄₅, r₄₆, r₅₆, то получим схему - рис. 1.2 б,

для которой затем определим их эквивалентные величины сопротивлений:

r₄₅ = (R₄+R₅) + (R₄R₅/R₆) = (2+4) + (2·4/8) = 7(Ом); (звезда → треугольник)

r₅₆ = (R₅+R₆) + (R₅R₆/R₄) = (4+8)+(4·8/2) = 28(Ом);

r₄₆ = (R₄+R₆) + (R₄R₆/R₅ = (2+8)+(2·8/4) = 14(Ом).

Затем, объединим параллельно и последовательно включенные резисторы и вычислим эквивалентное сопротивление схемы, которое составит: R_ЭКВ = 2,77 Ом.

2) Аналогично можно преобразовать соединенные треугольником резисторы R₁, R₄, R₅ в эквивалентное соединение звездой резисторов r₁₄, r₄₅, r₁₅ (рис 1.2,в), для которой сопротивления резисторов в эквивалентной схеме звезда, составят:

r₁₄ = R₁R₄/(R₁+R₄+R₅) = (6·2)/(6+2+4) = 1 (Ом); (треугольник → звезда)

r₄₅ = R₄R₅/(R₁+R₄+R₅) = (2·4)/(6+2+4) = 0,66 (Ом);

r₁₅ = R₁R₅/(R₁+R₄+R₅) = (6·4)/(6+2+4) = 2 (Ом).

Эквивалентное сопротивление R_ЭКВ в схеме на рис.1.2,б и рис.1.2,в – аналогично.

Если в схеме 1.2 вместо резисторов включены катушки индуктивностью L, то расчет их эквивалента L_Э выполняют аналогично резисторам [4]. Для подобных схем содержащих конденсаторы, способ расчета приведен в примере 1.3.

Пример 1.3. Пример оп­ределения эквивалентной емкости С_Э для схемы рис. 1.3.

Решение. Рассмотрим пример преобразования из схемы звезда в схему треугольник и обратно. Например, выполним замену емкостей С₃, С₅, С₈, соединенных по схеме звезда (рис. 1.3,а), в эквивалентное соединение по схеме треугольник С₃₅,С₅₈,С₃₈ (рис.1.3,б). Аналогично, выполним обратное преобразование – из схемы треугольник (рис.1.3,б - С₃₅, С₅₈, С₃₈), в схему звезда (рис.1.3,а - С₃, С₅, С₈).

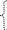( зв. → тр.) С₃₅ = С₃·С₅/(С₄+С₅+С₈); C₃₅ = (С₃+С₅)+(С₃·С₅/С₈); (тр.→зв.)

С₅₈ = С₅·С₈/(С₃+С₅+С₈); C₅₈ = (С₅+С₈)+(С₃·С₅/С₈);

С₃₈ = С₃·С₈/(С₃+С₅+С₈); C₃₈ = (С₃+С₈)+(С₃·С₈/С₅).

Часто в расчетной схеме к источнику ЭДС (Е) с внутренним сопротивление r_И подключен последовательно или параллельно эквивалент линии - элемент L_Э, C_Э.

После преобразования найдем эквивалентное реактивное Х или полное Z сопротивление всей цепи при последовательном или параллельном их включении.

Х _С.Э = 1/(2∙π∙f_(ГЦ)∙C_(Ф)), (Ом); Х_L.Э = (2∙π∙f_(ГЦ)∙L_(Гн)), (Ом); Z_Э = R² + Х_Э², (Ом);

Z_Э = R²∙Х_Э²/(R²+Х_Э²) (Ом); (для RL или RC элементов, включенных параллельно).

Пример 1.4. Определить параметры цепи (схема - рис.1.4) методом узлового напряжения и построить потенциальную диаграмму для приведенной схемы.

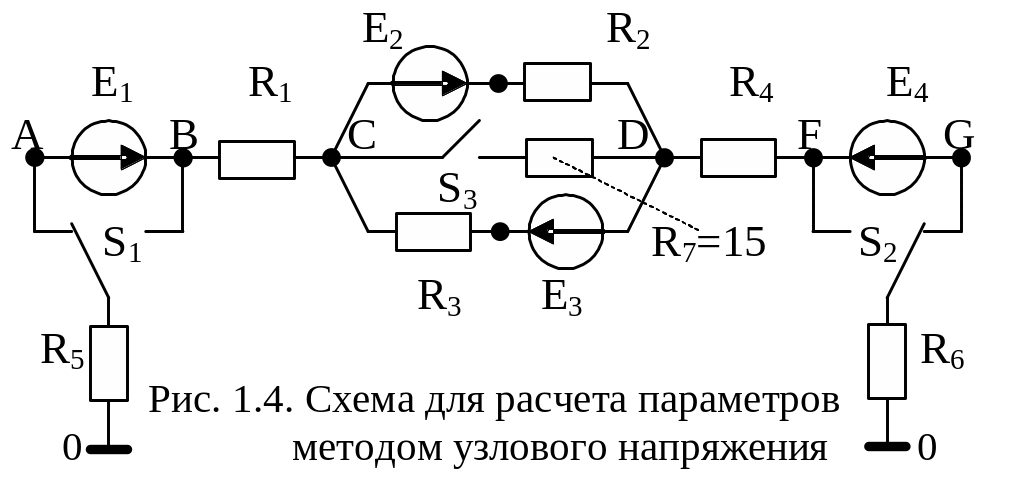
R₁ = 20; R₂ = 10; R₃ = 15;

R₄ = 9; R₅ =10; R₆ = 5 (Ом);

Е₁=15; Е₂ = 6; Е₃ = 8 (В);

Е₄ = 5,66 (В); R₇ = 15 (Ом);

Переключатели S₁ и S₁ – повернуты в положение ‘А’ и ‘G’. S₃ – отключен.

Найти: I_A = ? I_G = ?

U_AG = ? → U_Ri = ?

Решение. Вначале определим эквивалентное напряжение на участке CD:

U_CD = (Е₂/R₂ – Е₃/R₃)/[(1/R₂) + (1/R₃)] = [(6/10) – (8/20)]/[(1/10) + (1/20)] =

U_CD = (0,6 –0,4)/0,15 = 1,33 B. R_CD = (R₂·R₃)/(R₂ + R₃) = 6 (Ом).

2) Определим эквивалентное напряжение и ток при направлении обхода: A→G:

E_ЭКВ = Е₁– Е_CD – Е₄ = 15 – 1,33 – 5,66 = 8 B.

I = E_ЭКВ/R_ЭКВ = 8/(10+20+6+9+5) = 0,16 A.

U_AG = +Е₁–U_R1–E_CD –U_CD–U_R4–E₄ = Е₁–I·R₁ –E_CD–I·R_CD–I·R₄–E₄ = +2,4 B.

Определим разности потенциалов (φ_i - φ_J ) между соседними точками:

φ₀–φ_А– I·R₅ = 0; φ_А = φ₀– I·R₅; φ_А = 0–0,16∙10. φ_А = –1,6 v.

φ_А–φ_В + E₁ = 0; φ_В = φ_А + E₁. φ_В = –1,6 + 15. φ_В = +13,4 v.

φ_В–φ_С – I·R₁ = 0; φ_С = φ_В – I·R₁. φ_С = +13,4 – 3,2. φ_C = +10,2 v.

и так далее, до точки φ_G . Затем строят потенциальную диаграмму для рис. 1.4.

===========================================================================================================================================