Методические указания к выполнению контрольной работы

Задача № 1. Для плоской системы сходящихся сил определить аналитическим способом реакции стержней АВ и ВС кронштейна, удерживающего в равновесии груз G = 40 кН, проверить решение геометрическим способом.

В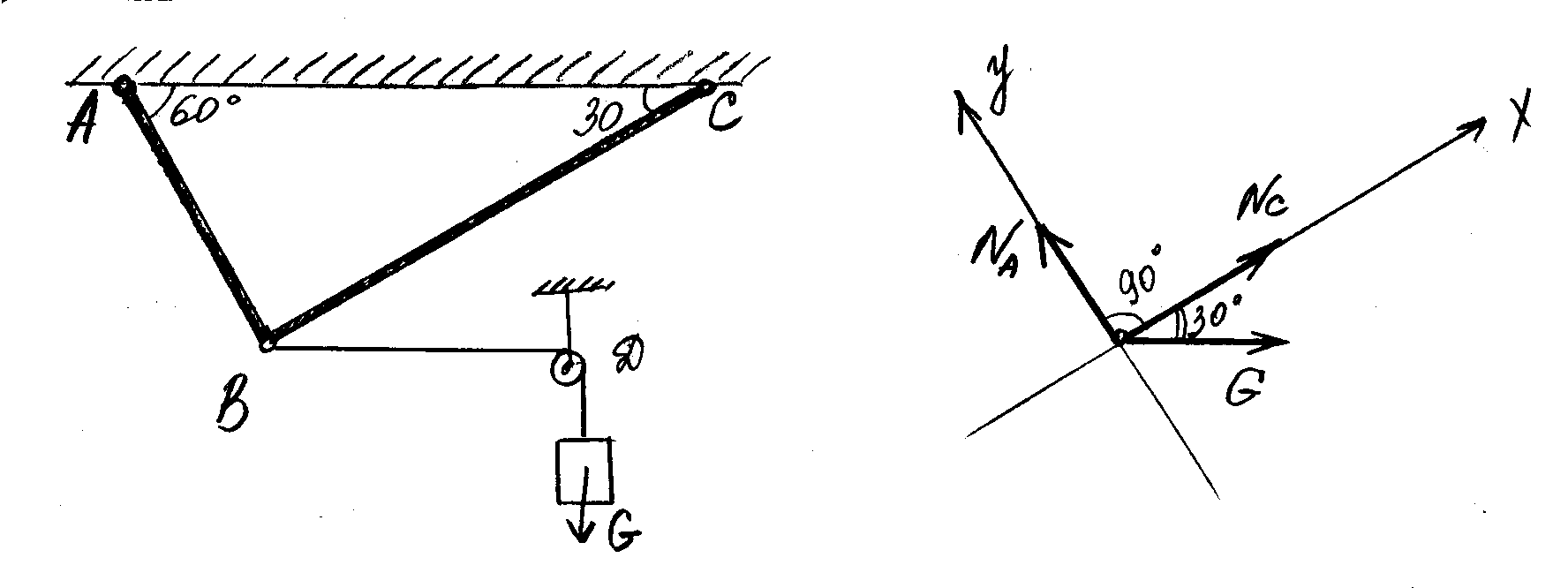

Рис. 1 рис. 2

1. Выделим точку, равновесие которой следует рассмотреть, чтобы определить реакции стержней. В данной задаче такой точкой является шарнир В. Изобразим его отдельно на рис. 2.

2. Укажем действующие на точку В активные силы (нагрузки). Такой силой является сила G, действующая вдоль нити, перекинутой через блок D.

3. Мысленно освободим шарнир В от связей (стержней и заменим действие связей их реакциями NA и NC, направленными вдоль стержней ВА и ВС соответственно. Не всегда заранее можно определить какой из стержней растянут или сжат. Поэтому существует общепринятое правило считать предположительно все стержни растянутыми. В соответствии с этим правилом реакции NA и NC стержней на рис. 2 направлены от шарнира В.

4. Приняв точку В за начало координат, выберем положение осей х (ось абсцисс) и у (ось ординат) таким образом, чтобы по крайней мере одна из них совпала с линией действия неизвестной силы, т.е. совместим одну из осей координат с осью какого-либо стержня. В нашем примере стержни АВ и ВС взаимно перпендикулярны, поэтому рационально провести через них оси отсчета.

5 . Определив при помощи данных на рис. 1 углы, образуемые силами G, NA, NC, с осями х и у, определим проекции всех сил на каждую из осей и составим из этих проекций уравнения для плоской системы сходящихся сил.

Σх = Nc + G · Cos30 = 0 (1)

Σу = NA - G · Cos60 = 0 (2)

6. Решаем получившуюся систему уравнений.

Из уравнения (1) имеем: Nc = - G · Cos30 = - 40·0,866 = - 34,64 кН

Знак минус перед численным значением Nc показывает, что вектор Nc должен быть направлен в противоположную сторону, т.е. стержень ВС не растянут, как предполагалось, а сжат силой 34,64 кН.

Из уравнения (2) имеем: NA = G · Cos60 = 40 · 0,5 = 20 кН

Численное значение NA положительно, значит выбранное направление вектора NA соответствует действительному и стержень ВА растянут силой 20 кН.

7. Решение задачи обязательно следует проверить. Лучшим способом проверки может быть либо решение с помощью иного выбора осей координат, либо решив задачу иным методом, например, графически.

G

с

30º

Nc

Na

90º

b

G = 40 кН

Nс = 34,64 кН

Na = 20 кН

а

рис. 3

Графическое решение задачи (оно показано на рис. 3) выполнять очень просто с помощью линейки с миллиметровой шкалой и транспортира.

1. Выбираем некоторый масштаб построения.

2. Из произвольной точки а откладываем горизонтально слева направо (так направлена сила G) вектор ас, который в выбранном масштабе изображает силу G. Из точек с и а проводим прямые, параллельные соответственно стержню ВА и стержню ВС. Эти прямые пересекаются в точке b. Образовался замкнутый многоугольник acb, в котором вектор аb изображает реакцию стержня ВА, а вектор bc – реакцию стержня ВС.

3. Измеряя искомые векторы, с учетом принятого масштаба получаем NA = 20кН, Nc = 34,64 кН. Следует отметить, что векторный многоугольник показывает действительное, а не предполагаемое направление искомых сил.

Задача № 2. Для балки (рис. а) определить реакции опор в точках А и В, если F = 16 кН, g = 2кН/м и М = 12 кН·м.

а)

б)

Р ешение. Рассматривая равновесие балки, освобождаем точки А и В от связей и заменяем связи силами реакций связей R_A и R_B (рис. б). Действие на балку равномерно распределенной нагрузки интенсивности g заменяем равнодействующей Q = g · 4 = 2 · 4 = 8 кН, которая расположена в середине длины этой нагрузки (рис. б). Таким образом, на балку действуют пара сил с моментом М и система параллельных сил R_A; Q; Р и R_B. Для определения неизвестных реакций связей балки и используем уравнения равновесия ∑М_A = 0 и ∑М_B = 0. В качестве проверочного уравнения принимаем уравнение ∑_у = 0. Выберем систему координат х и у с началом в точке А и составим уравнения равновесия системы сил:

∑М_A = 0 Q · 2 + М + F · 6 - R_B · 8 = 0 (1)

∑М_B = 0 R_A · 8 – Q · 6 + М – F · 2 = 0 (2)

∑_у = 0 R_A – Q F + R_B = 0 (3)

Из уравнения (1):

Из уравнения (2):

Из уравнения (3) следует, что

8,5 – 8 – 16 + 15,5 = 0

Следовательно, реакции R_A и R_B балки по величине и направлению определены верно.

Следует заметить, что момент М в отличие от сил не изменяет своего знака относительно точек А и В балки (и других произвольных точек) при написании уравнений моментов сил.

Задача № 3. Определить координаты центра тяжести сечения геометрической формы

П оложение центра тяжести фигуры сложной формы можно определить, разбив эту фигуру на пять элементов простой формы, положения центров тяжести которых известны:

I – прямоугольник 25 х 30 см с центром тяжести С₁

II – прямоугольник 55 х 10 см с центром тяжести С₂

III – прямоугольник 25 х 45 см с центром тяжести С₃

IV – два треугольника с центрами тяжести С₄ и С`₄

Нанесем на сечение координатные оси. Ось у совместим с осью симметрии сечения. Поскольку сечение симметрично относительно вертикальной оси и следовательно, х_с = 0, потребуется определить только координату у_с центра тяжести по формуле:

где S₁ S₂ S₃ S₄ – площади составных частей фигуры;

у₁ у₂ у₃ у₄ – ордината центра тяжести составных частей фигуры

относительно осей.

S₁ = 25 х 30 = 750 см² у₁ = 70 см

S₂ = 55 х 10 = 550 см² у₂ = 50 см

S₃ = 25 х 45 = 1125 см² у₃ = 22,5 см

у₄ = у`₄ = 30 см

Подставим числовые значения в формулу (1)

Итак, точка С имеет координаты

Х_с = 0

У_с = 40,5 см

Задача № 4. Для ступенчатого бруса требуется:

- построить эпюру продольных сил;

- построить эпюру нормальных напряжений;

- проверить прочность, если [δ]_р = 160 МПа и [δ]_cпc = 100 МПа;

- определить удлинение конца бруса, если Е = 2 ·10⁵ МПа, F₁ = 40 кН, F₂ = 10 кН, F₃= 50 кН, d₁ = 30 мм, d₂ = 20 мм.

Эδ(МПа)

Решение:

1. Разбиваем стержень на отдельные участки, начиная от свободного конца. Границами участков будут сечения, в которых приложены внешние силы или в которых изменяются размеры поперечного сечения стержня. В данном случае по длине бруса будет четыре участка.

Пользуясь методом сечений, определяем значение продольных сил в сечениях бруса, не определяя опорной реакции в его заделке. Проводя сечение в пределах первого участка и отбрасывая левую часть бруса, составим уравнение равновесия:

∑у = 0; – N₁ – F₁ = 0

откуда N₁ = – F₁ = – 40 кН

получили отрицательное значение. Следовательно, на первом участке брус сжат.

Проводим сечение на втором участке и отбрасываем левую часть бруса, получим уравнение равновесия для второго участка: – N₂ – F₁ + F₂ = 0, откуда N₂ = –F₁ + F₂ = –40 + 10 = – 30 кН.

Для четвертого участка уравнение равновесия имеет вид:

–N₄ –F₁ + F₂ + F₃ = 0, откуда N₄ = –F₁ + F₂ + F₃ = –40 + 10 + 50 = 20 кН

На четвертом участке стержень растянут. По полученным N₁, N₂, N₃, N₄ строим эпюру продольных сил.

2. Определяем нормальные напряжения по участкам, как отношение внутренних сил к площади поперечного сечения.

Площади поперечных сечений:

По полученным нормальным напряжениям строим эпюру .

3. Проверяем прочность ступенчатого бруса. Прочность бруса обеспечена, если выполняется условие: _max ≤ [].

Из эпюры нормальных напряжений выбираем максимальное нормальное напряжение на растяжение и сравниваем его с допускаемым:

/ _р/_max ≤ [ ]_р.

63,6 МПа ≤ 160 МПа

Условие прочности выполняется.

Из той же эпюры выбираем максимальное нормальное напряжение сжатия (по абсолютной величине) и сравниваем его с допускаемым.

/ _сж/_max ≤ [ ]_сж.

95,4 МПа ≤ 100 МПа

Условие прочности выполняется.

Вывод: прочность ступенчатого бруса обеспечена.

4. Так как ступени бруса изготовлены из одного материала, перемещ конца бруса определяем по формуле:

Вывод: брус укоротится на 0,032 мм.

Задача № 5. Для балки, изображенной на рис. а, построить эпюры Q и Мизг.

а)

Схема

нагружения бруса

б)

Расчетная схема

в)

г)

3,5

-8

Решение:

1 . Определяем опорные реакции

∑_mA = 0; –F₁ · 1 + F₂ · 3 – R_В · 4 + М = 0 (1)

∑_mВ = 0; R_А · 4 + F₁ · 3 – F₂ · 1 + М = 0 (2)

Из уравнения (1):

Из уравнения (2):

Проверка: условия равновесия балка

∑у = 0, R_А + F₁ – F₂ + R_В = –2,5 + 2 – 4 + 4,5 = 0

2. Обозначаем характерные точки балки. Характерными точками являются точки приложения сосредоточенных сил и моментов сил.

В данной задаче характерными являются точки: А, В, С, Д.

3. Строим эпюру поперечных сил. Следует учесть, что поперечная сила в сечении балки численно равна алгебраической сумме проекций внешних сил, лежащих по одну сторону от сечения на ось, перпендикулярную оси балки. силу, расположенную слева от рассматриваемого сечения и направленную вверх, считают положительной, а направленную вниз – отрицательной. Для правой части балки – наоборот (Q_Z=F_i отсеченная часть).

В сечениях, соответствующих точкам приложения сосредоточенных сил, в том числе в точках приложения опорных реакций, необходимо определить два значения поперечной силы: слева от рассматриваемой точки и справа от ее. Поперечные силы в этих сечениях обозначаются соответственно Q^лев. и Q^прав.

Найденные значения поперечных сил в характерных точках откладываются в некотором масштабе от нулевой линии. Соединив полученные значения прямыми линиями параллельными оси эпюры (рис. в) получим эпюру Qх.

4. Строим эпюру изгибающих моментов Мизг.

Для этого определяем изгибающие моменты в характерных точках АВСD.

Изгибающий момент в рассматриваемом сечении равен сумме моментов всех сил (сосредоточенных, в том числе опорных реакций, а также внешних сосредоточенных моментов), расположенных только слева от этого сечения. Если любое из перечисленных силовых воздействий стремится повернуть левую часть балки по часовой стрелке, то оно считается положительным, если против – отрицательным, а для правой части наоборот (М_Z= М(F_i) для отсеченной части).

В сечениях, соответствующих точкам приложения сосредоточенных моментов, необходимо определить два значения изгибающего момента: чуть левее рассматриваемой точки и чуть правее ее. Изгибающие моменты в этих точках обозначаются соответственно М^лев. и М^прав.

В точках приложения сил определяется одно значение изгибающего момента.

М_А = 0

М_С = R_А · 1 = – 2,5 · 1 = – 2,5 кН · м

М_Д = R_А · 3 + F₁ · 2 = – 2,5 · 3 + 2 · 2 = – 7,5 + 4 = –3,5 кН · м

М_В^лев. = R_А · 4 + F₁ · 3 – F₂ · 1 = – 2,5 · 4 + 2 · 3 – 4 · 1 = – 10 + 6 – 4 = –8 кН · м

М_В^пр. = R_А · 4 + F₁ · 3 – F₂ · 1 + М = – 2,5 · 4 + 2 · 3 – 4 · 1 + 8 = – 10 + 6 – 4 + 8= 0.

Полученные значения откладываются в некотором масштабе от нулевой линии. Соединяем полученные значения прямыми линиями, получаем эпюру Мизг (рис. г).