Общий интеграл этого уравнения имеет вид

Замечание. Если произведение X₁(x)•Y(у)=0 при х = а и у=b, то эти функции х=а и у=b являются решениями дифференциального урав­нения при условии, что при этих значениях х и у уравнение не теряет число­вого смысла. Геометрически эти решения представляют собой прямые,

парал­лельные осям координат.

Пример 2. Решить уравнение Найти частное решение, удовлетворяющее условию у = 3 при х = 22.

Решение. Так как то откуда (х²+1)dy=хуdх. Разделим обе части уравнения на произведение у(х² - 1):

Интегрируя, находим

После потенцирования получим решение откуда , или где С=+С₁.

Произведение у(х²+1)=0 при у = 0; так как при этом значении у дифференциальное уравнение не теряет числового смысла, то у = 0 — решение уравнения. Но оно входит в решение при С = 0. Значит, общее решение уравнения имеет вид .

Подставив в общее решение значения у=3 и х =22, получим 3=С•3, откуда С=1. Частное решение уравнения, удовлетворяющее данному условию, имеет вид

Пример 3. Решить уравнение 2х sin ydx +(х²+3) cos ydy=0. Найти частное решение, удовлетворяющее условию у =/2 при х=1.

Решение. Разделим каждый член уравнения на произведение (х² • +3)sin y:

Интегрируя, находим

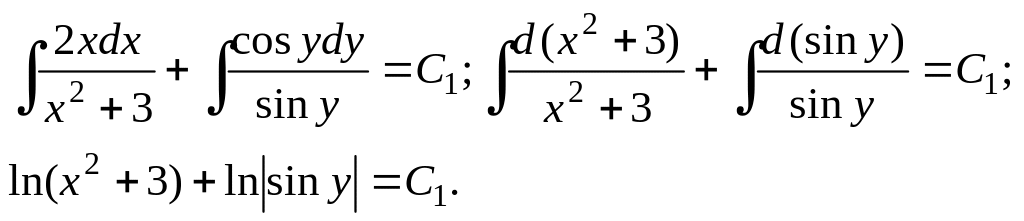
После потенцирования получим

или где . Отсюда

Произведение (х² + 3) sin у = 0 при sin у = 0, так как при этом значении дифференциальное уравнение не теряет числового смысла, то sin у=0 – решение уравнения. Но оно входит в интеграл при С=0. Значит, общий интеграл уравнения имеет вид .

Подставив в общий интеграл значения у=/2 и х=1, получим 1=С/(1+3), откуда С = 4. Частный интеграл уравнения, удовлетворяющий данному условию, имеет вид sin у = 4/(х² + 3).

Пример 4. Решить уравнение е^у (1 + х²) dy - 2x(1+е^у) dx =0. Найти частное решение, удовлетворяющее условию у=0 при х=0.

Решение. Перенесем второй член уравнения в правую часть и разделим обе части на произведение (1+е^у)(1+х²):

Интегрируя, находим

После потенцирования получим общий интеграл уравнения: 1 + е^у = С (1 + х²).

Подставив в общий интеграл значения у=0 и х=0, получим 1+1=С, откуда С=2. Частный интеграл уравнения, удовлетворяющий данному усло­вию, имеет вид 1+е^у=2(1+х²).

Вопросы для самопроверки

1. Какое уравнение называется дифференциальным?

2. Дайте определение дифференциального уравнения первого порядка.

3. Дайте определение общего решения и общего интеграла дифферен­циального уравнения первого порядка.

4. Дайте определение частного решения и частного интеграла дифферен­циального уравнения первого порядка.

5. Решите дифференциальные уравнения и найдите частные решения (частные интегралы), удовлетворяющие данным условиям:

а) (ху² + х) dx - (у – х²у) dy =0; у = 1 при х = 2.

б) е^х (1+е^у) dx + е^у(1 + e^x) dy = 0; у=0 при х=0,

6. Найдите частные решения (частные интегралы) дифференциального уравнения, удовлетворяющие данным условиям:

а) у' = у³/х³; у =2 при х =3;

б) у' tg х = 1 +у, у = - 1/2 при х = /6.

Ответы. 5. а) (1 + у²)(1 - х³) = С, (1 + у²)(1 - х³) = -6;

(1 + е^у)(1 - е^х) = С, (1 + е^у)(1 - е^х) = 4.

6. а) у²=6 х²/(х² +6); б) у=sin х –1.