Определенный интеграл
Понятие определенного интеграла. Непосредственное вычисление определенного интеграла производится по формуле Ньютона—Лейбница:
где а—нижний предел, Ь—верхний предел, F (x)—какая-нибудь первообразная функции f (х).
И
з
этой формулы виден порядок вычисления
определенного интеграл 1)
находят одну из первообразных
F (x)
данной функции;
2)
находят значение F
(x)
при х
=
а и х
=
Ь;
3)
вычисляют разность
F
(Ь)
— F
(а).
Пример 1. Вычислить интеграл
Решение. Воспользуемся определением степени с дробным и отрицательным показателем и вычислим определенный интеграл:
Приведем основные свойства определенного интеграла.
1. При перестановке пределов интеграла знак интеграла меняется на противоположный:
2
.
Отрезок интегрирования можно разбивать
на части:
3
.
Постоянный множитель можно выносить
за знак интеграла:
4. Интеграл от суммы функций равен сумме интегралов от всех слагаемых:
П
ример
2.
Вычислить интеграл
Решение. 1) Произведем подстановку х3+2=t; тогда
3х2dx=dt,
2) Определим пределы интегрирования для переменной t. При х=1 получаем tн=13+2=3, при х=2 получаем tв=23+2=10.
3) Выразив подынтегральное выражение через t и dt и перейдя к новым пределам, получим
Пример 3. Вычислить интеграл
Решение. 1) положим cos х=t; тогда – sinxdx =dt и
sinxdx = -dt. 2) Определим пределы интегрирования для переменной t: tн=cos0=1:tв=cos (π/2)=0.
3) Выразив подынтегральное выражение через t и dt и перейдя к новым пределам, получим
Пример 4. Вычислить интеграл
Решение. Сначала преобразуем подынтегральное выражение
sin3x = sin2 x • sin x = (1 — cos2x) sin x = sin x - cos2 x sin x.
Затем вычислим интеграл от разности функций, заменив его разностью определенных интегралов от каждой функции:
Вычислим каждый интеграл отдельно:
-
cos x =t,
-sin xdx =dt,
sin xdx =-dt,
tн=cos0 =1
tв=cos(π/2) =0.
Тогда
Приложения определенного интеграла. Площадь плоской фигуры. Площадь криволинейной трапеции аАВЬ (рис. 46), ограниченной гpaфикoм непрерывной функции y=f(x), где
хЄ[а, b], отрезком [a,b] оси Ох, отрезками прямых х =a и х = b, вычисляется по формуле
(1)
Пример 5. Вычислить площадь фигуры, ограниченной параболой у = х2 , прямыми х = - 1, х = 2 и осью абсцисс (рис.47).
Решение. Применяя формулу (1), получаем
т.е. S=3 кв. ед.
Площадь фигуры ABCD (рис. 48), ограниченной графиками непрерывных функций у =f1(x) и у f2= (x), где х Є[а, b], отрезками прямых х = а и х = Ь, вычисляется по формуле
(2)
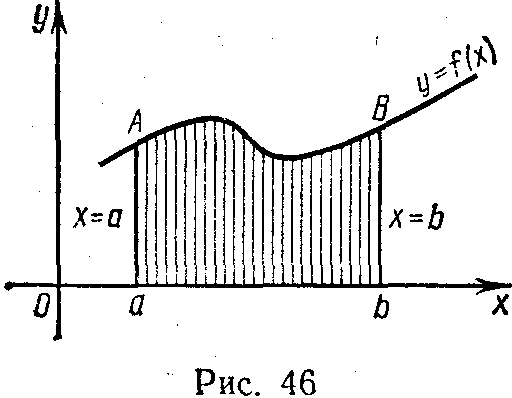
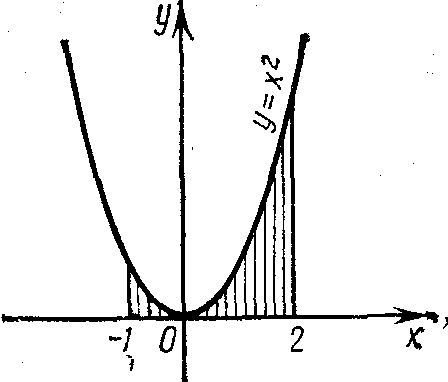
рис.
46
рис.
47
Пример 6. Вычислить площадь фигуры, ограниченной осью Ох и линией у = х2 — 2х (рис. 49).
Решение. Найдем пределы интегрирования, т. е. абсциссы точек пересечения графиков функций y=х2—2х и у=0 (ось Ох). Для этого решим систему
Теперь найдем искомую площадь:
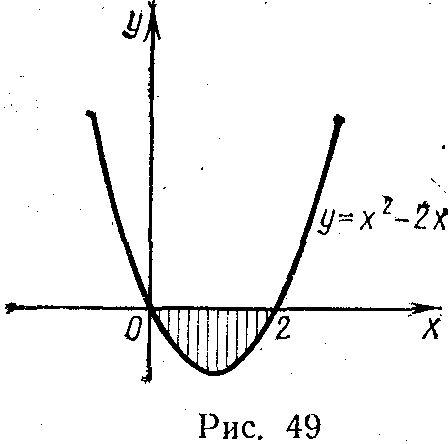
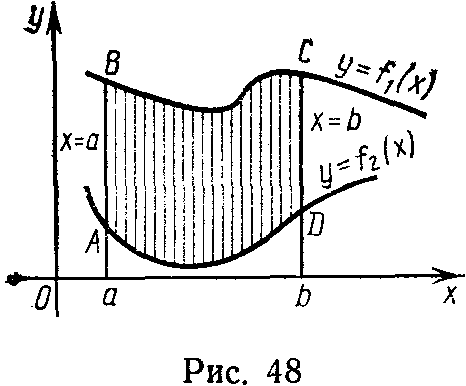
рис.
48
рис.
49
Пример 7. Вычислить площадь фигуры, ограниченной линиями у = х2 и у2 =х (рис. 50).
Решение. Найдем пределы интегрирования, т. е. абсциссы точек пересечения графиков функций у = х2 и у2 =х. Для этого решим систему
Искомую площадь вычисляем по формуле (2) при f1(x)=x2,
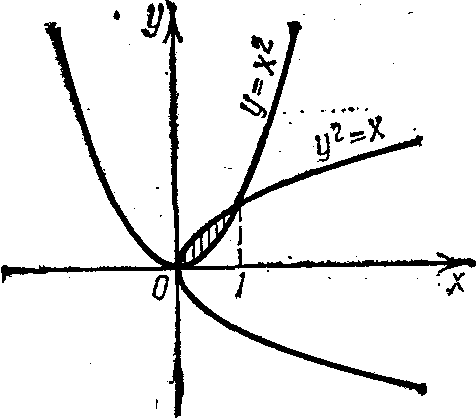
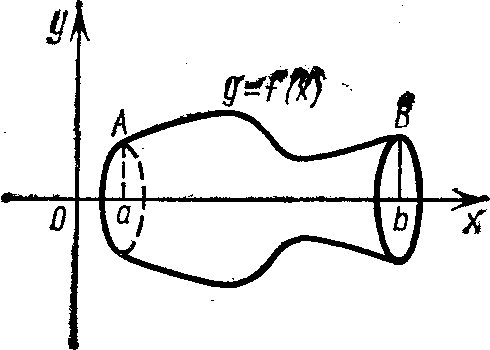
рис.
50
рис.
51
Объем тела вращения. Объем тела, образованного вращением вокруг оси Ох криволинейной трапеции аАВЬ, ограниченной непрерывной кривой у = f (x), где x Є [а, b], отрезком [а, Ь] оси Ох, отрезками прямых х = а и х = b (рис. 51), вычисляется по формуле
(3)
Пример 8. Вычислить объем тела, образованного вращением вокруг ocи Ох фигуры, ограниченной параболой у2=2х, прямой х = 3 и осью Ох (рис. 52).
Решение. Применяя формулу (3), находим искомый объем:
(куб. ед.)
Объем тела, образованного вращением вокруг оси Оу криволинейной трапеции аАВЬ, ограниченной непрерывной кривой x=f(y), где у Є [а, b], отрезком [а, b] оси Оу, отрезками прямых у = а и у = Ь (рис. 53), вычисляется по формуле
(4)
Пример 9. Вычислить объем тела, образованного вращением вокруг ocи Оу фигуры, ограниченной параболой у=х2 и прямой у = 4 (рис. 54).
Решение. Применяя формулу (4), находим искомый объем:
(куб. ед.)
Путь, пройденный точкой. Если точка движется прямолинейно и ее скорость v=f(t) есть известная функция времени t, то путь пройденный точкой за промежуток времени [t1,t2], вычисляется по формуле
(5)