IV. Обыкновенные дифференциальные уравнения.

Определение обыкновенного дифференциального уравнения. Част­ное и общее решение. Уравнения с разделенными и разделяющимися переменными. Однородные уравнения 1-го порядка, уравнения, приводящиеся к однородным. Уравнения в полных дифференциалах. Линейные уравнения 1-го порядка.

Линейные однородные уравнения высших порядков. Фундамен­тальная система решений.

V. Элементы теории вероятностей и математической статистики.

Опыт. Событие. Виды событий. Случайные события. Виды случайных событий. Относительная частота появления события. Классические определения вероятности. Основные понятия комбина­торики. Операции над событиями. Теоремы сложения и умножения вероятностей.

Противоположные события. Повторные независимые испытания. Формула Бернулли.

Дискретная случайная величина, закон ее распределения. Числовые характеристики распре­деления дискретной случайной величины.

Понятие о законе больших чисел. Понятие об основных задачах математической статистики. Выборочный метод, репрезентативность выборки.

VI. Элементы вычислительной математики

Действия над приближенными числами. Вычисления с заданной точностью, с точным учетом и без точного учета погрешности.

Вычисления на логарифмической линейке и на малых вычисли­тельных машинах. Вычисления с помощью таблиц. Вычисление зна­чений функции по заданной формуле. Решение задач прикладного характера.

МЕТОДИЧЕСКИЕ УКАЗАНИЯ К ВЫПОЛНЕНИЮ КОНТРОЛЬНОЙ РАБОТЫ

Функции. Последовательности. Пределы.

Необходимо хорошо усвоить теоремы о пределах:

1. lim (x+y-z)=lim x + lim y – lim z.

2. lim c =c, c-const.

3. lim (xy)=lim x lim y, lim (cx)=c lim x .

4. lim x/y)=lim x / lim y, если lim y =0.

5. lim (x^m)= (lim x)^m.

Приступим к отысканию пределов функций. Вопрос о пределе функции не имеет смысла, если не указан предел аргумента. Рассмотрим решение примеров.

Пример 1. Вычислить .

Решение. Применяя теоремы 1, 2, 3, 5, запишем

Пример 2. Вычислить

Р ешение

Пример 3. Вычислить

Решение

Пример 4. Вычислить

Р ешение. В данном случае теорема о пределе частного не применима, так как Числитель дроби разложим на

множители и сократим дробь на (х -I):

Допредельное значение х-1=0, поэтому сокращение на (х -1) законно.

Пример 5. Вычислить

Решение. Разделим числитель, и знаменатель дроби на х⁴:

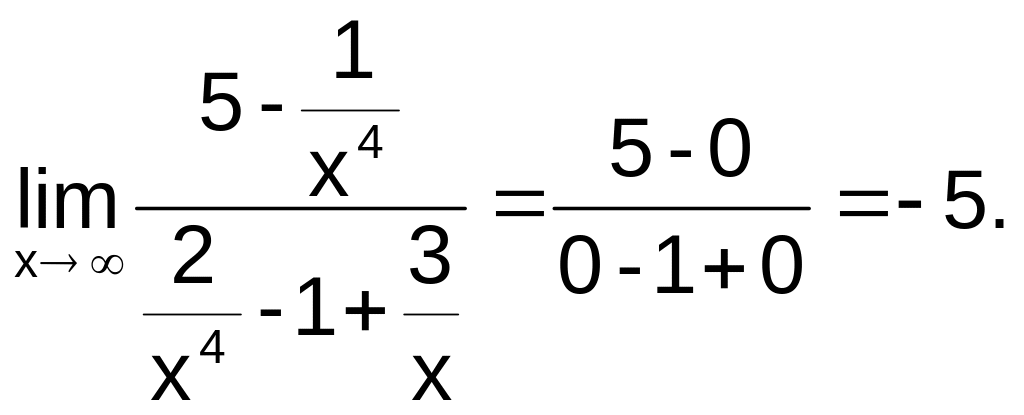
Пример 6. Вычислить

Решение. Заменим sin Зх эквивалентной бесконечно ма­лой Зх:

Пример 7. Вычислить

Р ешение.

Вопросы для самопроверки

1. Дайте определение функции.

2. Перечислите способы задания функции. Приведите примеры.

3. Сформулируйте определение числовой последовательности.

4. Какие бывают числовые последовательности?

5. Сформулируйте теорему о существовании предела последовательности.

6. Какая существует зависимость, между бесконечной малой и бесконечно большой последовательностями?

7. Дайте определение предела переменной.

8. Напишите уравнение гармонического колебания.

9. Как определяются функции y==arcsin х, y=arccos x,

у= =arctg x, у=arcctg х?

10. Чему равно выражение y=sin(arcsin x)?

11. Как найти приращение аргумента?

12. Как найти приращение функции?

13. Как вычисляется средняя скорость изменения функции?

14. Дайте определение производной функции.

15. Выпишите теоремы о производных алгебраической суммы, произведения, частного.