МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ УКРАИНЫ
СЕВАСТОПОЛЬСКИЙ НАЦИОНАЛЬНЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
Кафедра кибернетики и
вычислительной техники
Контрольная работа
по дисциплине
«Цифровая обработка сигналов»
Выполнил:
студент группы М-61з
Паращук И.М.
Проверил: _____________
Севастополь
2013
Контрольное задание №1
Цель работы: Освоение методики применения дискретного преобразования Фурье (ДПФ) и исследование его свойств на конкретных примерах.
Основные теоретические положения
Основу дискретизации сигналов во времени составляет теорема Котельникова-Шеннона, которая в качестве условия восстановления непрерывного сигнала по его дискретным значениям выдвигает требование осуществления выборки с шагом
,
где F – частота выборки Найквиста.
Если частота выборки больше величины частоты Найквиста, спектр непрерывного сигнала может быть восстановлен по спектру дискретного.
Для определения частоты Найквиста, необходимо рассматривать спектр исходного сигнала. Частота Найквиста выбирается не меньше максимальной частоты в спектре.
Соотношения, определяющие прямое и обратное ДПФ, можно определить следующим образом:
,
,
где:
Xk – элемент выборки изображения по Фурье,
xi – выборка исходного сигнала,
N – количество точек выборки.
Здесь шаги
дискретизации рассчитываются как
Вариант задания
Сигналы заданы в виде их преобразований по Лапласу.
Исходное изображение
по Лапласу: f=
Возьмем a=0.5.
Ход работы
Для исходного изображения найдем обратное преобразование Лапласа (оригинал):
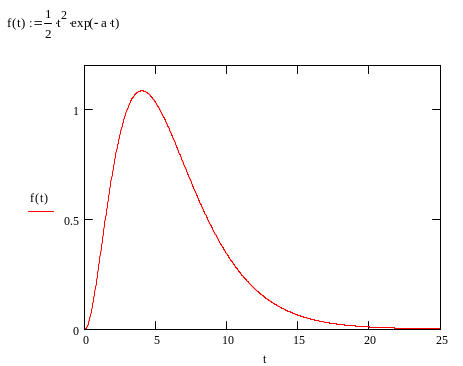
Рис1. – График функции оригинала.
Построим график спектральной характеристики сигнала.
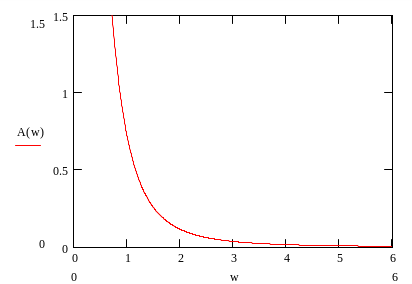
Рис2. – Спектральная характеристика исходного сигнала.
Спектр симметричен и лежит в диапазоне частот [-5; 5].
Исходя из значения максимальной частоты в спектре, выберем частоту Найквиста:
Здесь М – удвоенная частота Найквиста.
Количество точек выборки:
,
где Т – период исходного сигнала (Т=20).
Построим спектральную характеристику для дискретной выборки с частотой Найквиста.
Для анализа зависимости характеристик сигнала от частоты дискретизации, проведем повторно данные расчеты для частоты Найквиста большей и меньшей исходной.
Приведем расчеты, составленные в системе MathCad.
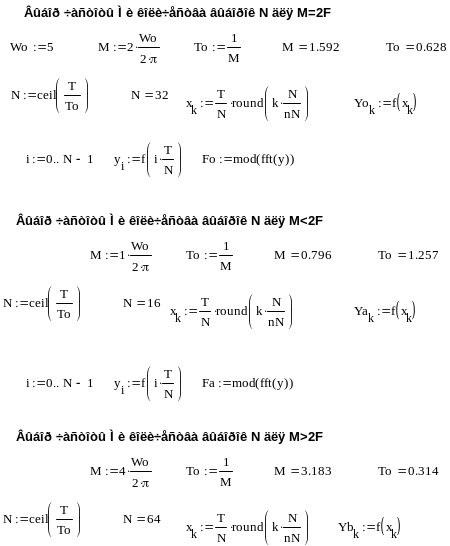
Для трех выборок построим полученный исходный дискретизированный сигнал.
Рис3. – Дискретные выборки и исходный сигнал.
Для наглядности на рисунке показана только часть периода сигнала.
На рисунке показаны следующие функции:
Yo – выборка для исходной частоты Найквиста;
Ya – выборка для частоты дискретизации ниже исходной;
Yb – выборка для частоты дискретизации выше исходной;
f(x) – непрерывная исходная функция сигнала;
Как видно из рисунка, чем больше частота дискретизации, тем большее количество выборок производится на функции. Чем больше выборок производится, тем точнее дискретный сигнал представляет исходный аналоговый.
Построим графики спектра дискретных сигналов.
Рис4. – Спектр дискретных сигналов.
На рисунке показаны следующие функции:
Fo – спектр выборки для исходной частоты Найквиста;
Fa – спектр выборки для частоты дискретизации ниже исходной;
Fb – спектр выборки для частоты дискретизации выше исходной;
Как видно из рисунка, чем больше частота выборки, тем более точно спектр дискретной выборки приближается к спектру аналогового сигнала.
Вывод
В ходе выполнения данного контрольного задания были освоены методики применения дискретного преобразования Фурье (ДПФ) и исследование его свойств на конкретных примерах.
Результаты исследования показали, что «реалистичность» дискретного сигнала по отношению к аналоговому (исходному) пропорциональна частоте выборок сигнала.
Чем больше частота выборки, тем меньше искажений в характеристиках сигнала.