10 Клас

1. Для шести цілих чисел a, b, c і A, B, C справджуються співвідношення:

, , , .

Знайдіть числа a, b, c, для яких сума набуває найменшого можливого значення.

Відповідь: .

Розв’язання. Розв’яжемо задану систему рівнянь відносно чисел a, b, c. З перших двох рівнянь маємо, що . Додаємо це до третього рівняння і знаходимо, що

.

Аналогічно або з міркувань симетрії знаходимо, що

та .

Найменша можлива сума досягається для трьох найменших різних квадратів цілих чисел: . Але для такої трійки квадратів числа a, b, c не будуть цілими, наприклад . Наступна за величиною суми трійка квадратів — числа . Для цієї трійки значення a, b, c є цілими, а отже шуканими:

, , .

2. (Рубльов Богдан) Послідовність дійсних чисел , , , ..., задовольняє умови:

.

Яких значень може набувати різниця ?

Відповідь: 0.

Розв’язання. Нехай . Можемо записати рівності:

...,

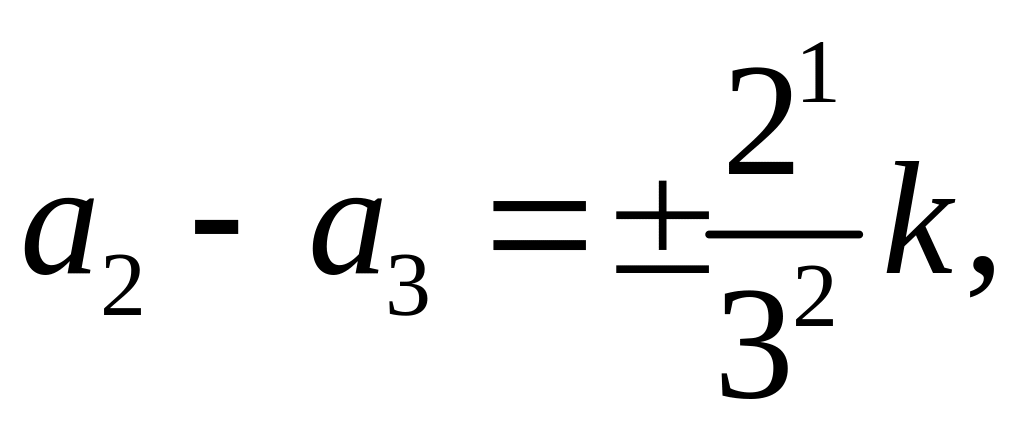Якщо , додамо ці рівності і скоротимо все на k, унаслідок чого матимемо таку рівність:

.

Але незалежно від знака перед 1 ми не можемо одержати в результаті 0, адже модуль суми решти доданків менший за 1. У цьому легко переконатися з допомогою формули для суми членів геометричної прогресії:

.

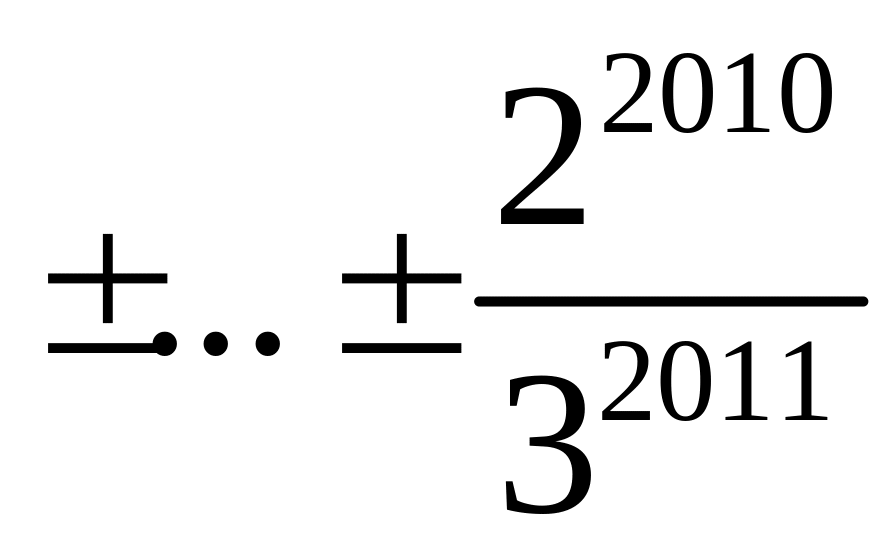
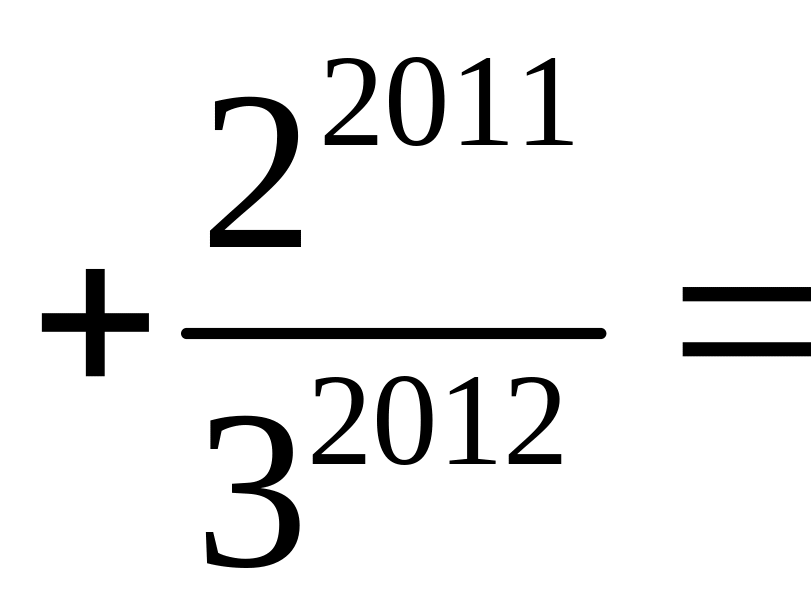
Отже, випадок неможливий. Тоді , звідки , тобто .

3. Для кожного натурального n знайдіть кількість наборів , які є перестановками чисел і задовольняють умову:

.

Відповідь: при є один набір, що задовольняє умову задачі; при — два набори; при інших значеннях n таких наборів не існує.

Розв’язання. При існує тільки тривіальна перестановка (1), яка, очевидно, задовольняє умову. Хай . Тоді і для всіх можливих перестановок, а тоді й лише тоді, коли — парне, тобто дорівнює 2. Тож маємо дві перестановки, що задовольняють умову: (1, 3, 2) і (3, 1, 2).

Нехай тепер або і — набір чисел, який задовольняє умову. Тоді сума повинна ділитися на n. Якщо n — парне, тобто , то , суперечність. Таким чином, парним n бути не може.

Хай тепер — непарне число, тобто , . Тоді , і для має виконуватись умова . Перепишемо її таким чином:

.

Оскільки , то , і цей вираз може ділитися на лише за умови, що він дорівнює 0, тобто , а .

Аналогічно, . Звідси маємо, що

.

Оскільки , то , а враховуючи, що , цей вираз може ділитися на лише за умови, що він дорівнює 0, тобто також дорівнює . Але це неможливо, оскільки серед чисел набору значення має траплятися рівно один раз. Одержана суперечність показує, що і для непарного наборів, які задовольняють умову задачі, не існує.

4. (Рожкова Марія) У трикутнику ABC зі сторонами розглядаються кути між висотою та медіаною, що проведені з однієї вершини. З’ясуйте, при якій вершині цей кут є найбільшим із трьох.

Відповідь: при вершині B.

Р озв’язання. Позначимо стандартним чином сторони трикутника через a, b, c. Тоді за умовою . Позначимо висоту та медіану з вершини B через та відповідно (рис. 7). Тоді кут, який нас цікавить, — це , при цьому . Аналогічно визначаються косинуси інших досліджуваних кутів. Щоб довести, що саме при вершині B кут найбільший, достатньо показати, що косинус цього кута — найменший, тобто 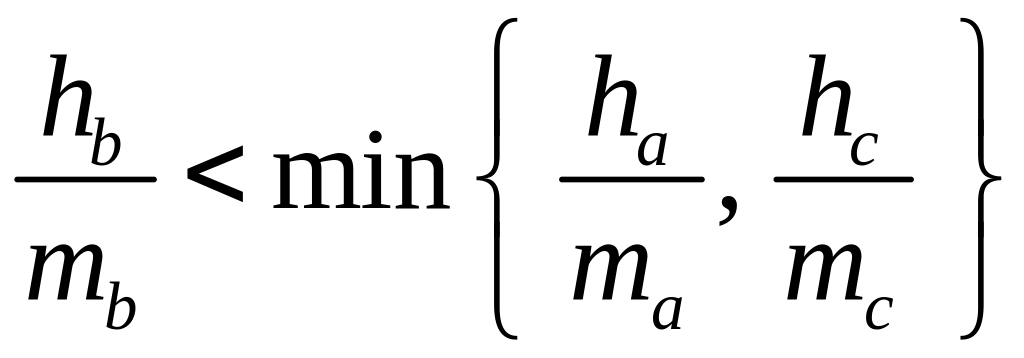. Доведемо для цього, що

та .

Щоб це зробити, використаємо такі формули для обчислення висоти та медіани:

та .

Перша нерівність еквівалентна такій:

.

Остання нерівність справджується, оскільки за умовою .

Аналогічно, для другої нерівності маємо:

.

Остання нерівність, знову ж таки, справджується, оскільки .

5. (Мисак Данило) Яку найбільшу кількість точок можна розташувати на площині так, щоб існувало рівно 2012 прямих, які проходять хоча б через дві з них?

В ідповідь: 2012 точок.

Розв’язання. Розташувати 2012 точок так, щоб була виконана умова задачі, досить просто: 2011 точок розмістимо на одній прямій, а останню точку — поза нею (рис. 8). Доведімо, що розташувати на площині більше за 2012 точок, задовольнивши умову задачі, неможливо.

Лема. Якщо на площині задана множина M, що складається з n точок, не всі з яких лежать на одній прямій, то існує пряма, яка проходить рівно через дві точки із заданої множини M.

Д оведення. Проведемо всі прямі через кожні дві точки множини M. Знайдемо таку проведену пряму і таку точку із M, відстань між якими найменша (при цьому, звичайно, не розглядається жодна така пара з точки та прямої, що точка лежить на прямій). Позначимо відповідну пряму як l, а точку — як A. Доведемо методом від супротивного, що на прямій l лежить тільки дві точки із M. Припустимо, що на ній лежить принаймні три точки з цієї множини, й позначимо їх «зліва направо» через , і (рис. 9). Оскільки , то або , або . Без обмеження загальності можемо вважати, що . Нехай — висота трикутника , опущена з вершини A, а — висота цього трикутника, опущена з . Позаяк площа трикутника дорівнює і , то . Але це означає, що відстань між точкою і прямою менша за відстань між A і l. Одержана суперечність завершує доведення леми.

Покажемо тепер, що якщо на площині розташовано n точок, то або всі вони лежать на одній прямій, або існує щонайменше n прямих, які проходять хоча б через дві з них. Це означатиме, що якщо на площині розміщено більше за 2012 точок, то пряма буде або одна, або їх буде більше за 2012.

Доведення проведемо методом математичної індукції. Для твердження очевидне. Нехай це твердження справджується для деякого n. Покажемо, що воно виконується також і для . Розглянемо довільну точку, не всі з яких лежать на одній прямій. Виберемо дві точки, на прямій із якими не лежить жодна інша точка множини (згідно з доведеною лемою це завжди можна зробити). Приберімо одну з цих точок, до того ж виберемо таку, щоб решта точок не лежали на одній прямій. Після цього залишиться n точок, не всі з яких лежать на одній прямій. Вони, згідно з індукційним припущенням, утворюють щонайменше n прямих. Але серед цих прямих нема тієї, що проходить через дві вибрані точки, одну з яких було вилучено. У сумі з нею прямих буде не менше ніж . Індукційний перехід доведено.