Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Российский государственный университет правосудия

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Matematika-Uch_posob_dlya_SE.doc

Скачиваний:

Добавлен:

01.05.2025

Размер:

9.17 Mб

Скачать

☆

<<< < Предыдущая 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 3839 / 4339 40 41 42 43 > Следующая >>>

Тест 5. Основы дифференциального исчисления

А. Производная функции

Задача. Вычислить производную от f(x) номер W.

0. f(x)sin(x²) . 1. f(x) .

2. f(x) . 3. f(x) .

4. f(x) . 5. f(x) .

6. f(x) . 7. f(x) .

8. f(x)ln²(x)(x⁴3). 9. f(x)cos(x²) .

10. f(x)tg(x²)(x3)². 11. f(x) .

12. f(x) . 13. f(x) .

14. f(x) . 15. f(x) .

16. f(x) . 17. f(x) .

18. f(x) . 19. f(x) .

Пример. W18.

f(x) .

Решение.

f’(x)  



 



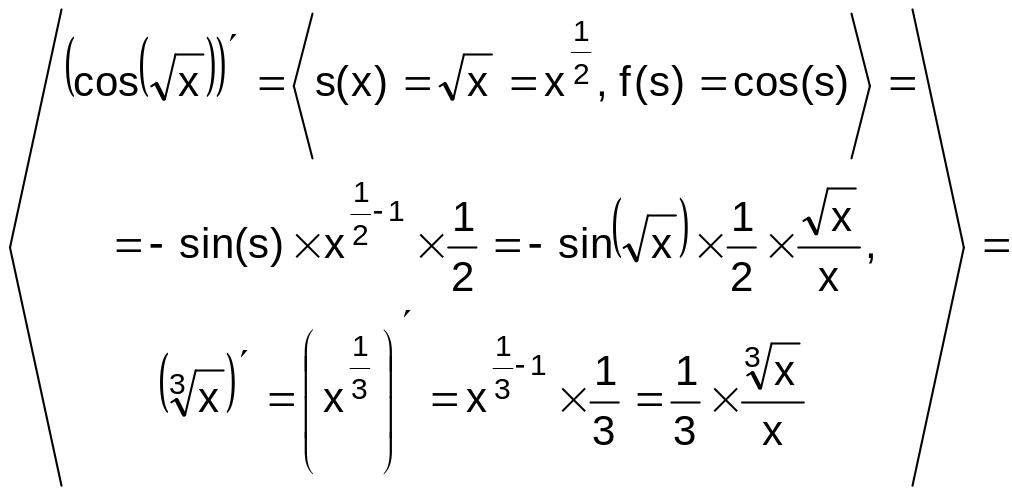
Б. Экстремумы функций

	Таблица к тесту 5,б
W	f(x)	W	f(x)
0	5x³18x²7x6	10	3x³16x²x40
1	4x³9x²58x15	11	2x³6x²48x5
2	3x³2x²53x60	12	5x³19.5x²18x40
3	2x³5x²x2	13	4x³7x²62x15
4	5x³34x²53x2	14	3x³5x²16x12
5	4x³11x²6x9	15	2x³27x²108x120
6	3x³16x²x60	16	5x³8x²19x6
7	2x³3x²36x3	17	4x³6.5x²4x3
8	5x³34x²53x12	18	2x³15x²36x27.5
9	4x³31x²52x15	19	x³3.5x²6x11

Задача. Найти экстремумы функции f(x) номер W.

Пример. W18. f(x)x³0.5x²4x1.

Решение. f(x) – кубическая парабола, особенностей не имеет.

Находим нули производной от f(x).

f’(x)3x²x4.

3x²x40. 3x²x40.

x₀  , x₁ 1.

Для проведения дополнительных исследований нанесем на числовую ось сетку чисел с шагом так, чтобы на ней разместились корни x₀ и x₁, а также удобные числа слева и справа от каждого из корней (рис. Э).

Отступаем от корня x₀ в точку x_L 2. Здесь f’(2)60. Отступаем от корня x₀ в точку x_R0. Здесь f’(0)40.

Значит, корень x₀ – точка минимума функции f(x).

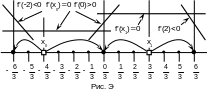Отступаем от корня x₁ в точку x_L0. Здесь f’(0)40. Отступаем от корня x₁ в точку x_R 2. Здесь f’(2)100.

Значит, корень x₁ – точка максимума функции f(x).

Тест 6. ОСНОВЫ ИНТЕГРАЛЬНОГО ИСЧИСЛЕНИЯ

Определенный интеграл

Задача. Вычислить среднее значение Y_ср для функции f(x) номер W на отрезке [a, b]

а) по формуле Ньютона-Лейбница,

б) методом Рунге-Ромберга по формуле трапеций.

f(x) , a1.0, b3.0.
f(x) , a1.2, b3.6.
f(x)cos²(x)sin(x), a0.0, b1.2.
f(x) f(x)x²e^-x, a0.0, b8.0.
f(x)sin²(x)cos(x), a1.2, b3.6.
f(x)x , a2.0, b0.0.
f(x) , a5.0, b1.0.
f(x) , a9.0, b1.0.
f(x) , a0.8, b0.8.
f(x) , a0.0, b6.0.
f(x)8x² 8 , a0.4, b2.0.
f(x)8  , a6.5, b2.5.
f(x) , a0.0, b6.0.
f(x) , a4.0, b10.0.
f(x) , a6.0, b0.0.
f(x) , a1.8, b0.2.
f(x) , a1.0, b0.2.
f(x) , a3.2, b0.0.
f(x) , a1.0, b7.0.
f(x) , a12.0, b20.0.

Пример. W18.

f(x)3x⁵cos(x³), a1.1, b1.7.

Решение. Вычислим площадь

F

а) по формуле Ньютона-Лейбница: FF_NL F(b)F(a).

1-й этап.

F(x) 

 

  

 

tsin(t) tsin(t)cos(t)F(t).

Найдем пределы по переменной t:

xa1.1, a_t 1.33, xb1.7, a_t 4.91.

2-й этап.

FF_NL  

 

sin(4.91)0.98, cos(4.91)0.20,

sin(1.33)0.97, cos(1.33)0.24

(4.820.20)(1.290.24)6.15.

Итак, F_NL6.15. Y_срY_NL  10.25.

б) методом Рунге-Ромберга по формуле трапеций.

1. Функцию f(x) на отрезке [a,b] представляем таблицей {xt_i,yt_i} объемом n4.

h 0.15.

xt₀a1.10, xt_ixt_i_₁h, i , (xt_nb1.70),

yt_if(xt_i), i .

Результат нашей работы показан ниже.

i	0	1	2	3	4
xt_i	1.10	1.25	1.40	1.55	1.70
yt_i	1.15	3.42	14.88	22.42	8.49
j	0		1		2

2. Вычисляем значение определенного интеграла по формуле трапеций на шаге h:

F_h 

 5.38.

3. Оставляем в таблице отсчеты с четными номерами i, заново их нумеруем (j). Теперь объем таблицы равен n2 2, ее шаг h22h0.30, а отсчеты обозначим как yt2_j. Вычисляем значение определенного интеграла на шаге h2:

F₂_h 