
- •Предисловие
- •Введение
- •Раздел I основания математики Глава 1. Элементы теории множеств
- •1.1. Понятие множества
- •1.2. Операции над множествами
- •1.3. Аксиомы и теоремы алгебры множеств
- •Глава 2. Числа
- •2.1. Системы счисления
- •2.2. Классы чисел
- •2.3. Элементы статистической обработки данных
- •2.4. Алгоритмы решения вычислительных задач
- •Глава 3. Элементы математической логики
- •3.1. Понятие высказывания
- •3.2. Операции над высказываниями
- •2.3. Аксиомы и теоремы алгебры логики
- •Раздел II основы математического анализа Глава 4. Функции
- •4.1. Понятие функции
- •4.2. Аппроксимация функций
- •4.3. Предел функции
- •Глава 5. Основы дифференциального исчисления
- •5.1. Производная функции
- •5.2. Свойства дифференцируемых функций
- •5.3. Дифференциал функции
- •Глава 6. Основы интегрального исчисления
- •6.1. Определенный интеграл
- •6.2. Машинные алгоритмы вычисления определенных интегралов
- •Раздел III основы теории вероятностей Глава 7. Понятие вероятности
- •7.1. Элементы комбинаторики
- •7.2. Случайные события
- •7.3. Классическое определение вероятности
- •7.4. Теорема умножения вероятностей
- •7.5. Основные формулы теории вероятностей
- •Глава 8. Случайные величины
- •8.1. Понятие случайной величины
- •8.2. Законы распределения случайных величин
- •8.3. Числовые характеристики случайных величин
- •8.4. Канонические распределения случайных величин
- •8.5. Энтропия и информация
- •Раздел IV. Основные способы и методы защиты информации Глава 9. Основы криптографической защиты информации
- •9.1. Принципы и основные понятия криптографической защиты информации
- •9.2. Основные понятия и определения
- •Глава 10. Методы криптографической защиты информации
- •10.1. Методы перестановки
- •10.2. Метод гаммирования
- •Ответы к задачам
- •Раздел I.
- •Глава 1. Элементы теории множеств
- •Глава 2. Числа
- •Глава 3. Элементы математической логики
- •Раздел II. Основы математического анализа
- •Глава 4. Функции
- •Глава 5. Основы дифференциального исчисления
- •Глава 6. Основы интегрального исчисления
- •Раздел III. Основы теории вероятностей
- •Глава 7. Понятие вероятности
- •Глава 8. Случайные величины
- •Глава 9. Основы криптографической защиты информации
- •Глава 10. Методы криптографической защиты информации
- •Приложение тесты
- •Тест 1. Элементы теории множеств
- •Тест 4. Функции
- •Тест 5. Основы дифференциального исчисления
- •Определенный интеграл
- •Тест 7. Понятие вероятностй
- •Тест 8. Случайные величины
- •Тест 10. Методы криптографической защиты информации
- •Литература
- •Сведения об авторах
- •Королёв Владимир Тимофеевич, Ловцов Дмитрий Анатольевич,
- •Математика и информатика Часть первая
Тест 4. Функции
А. Аппроксимация функций
Задача. По заданному выражению f(x) построить на отрезке [a,b] таблицу объемом n.
Выполнить линейную аппроксимацию этой табличной функции, найти приближенные значения y по аппроксимирующим формулам и точные значения yT по заданному выражению f(x) для x{x1,x2}.
Оценить погрешность аппроксимации.
f(x)
 ,
a1.0,
b3.0,
x11.7,
x23.5.
,
a1.0,
b3.0,
x11.7,
x23.5.f(x)
 ,
a0.5,
b4.5,
x12.0,
x25.5.
,
a0.5,
b4.5,
x12.0,
x25.5.f(x)cos2(x)sin(x), a0.3, b1.5, x10.2, x21.4.
f(x)x2e-x, a0.0, b8.0, x13.0, x29.0.
f(x)sin2(x)cos(x), a0.4, b2.0, x11.0, x22.2.
f(x)x
 ,
a2.0,
b0.0,
x10.8,
x20.3.
,
a2.0,
b0.0,
x10.8,
x20.3.f(x)
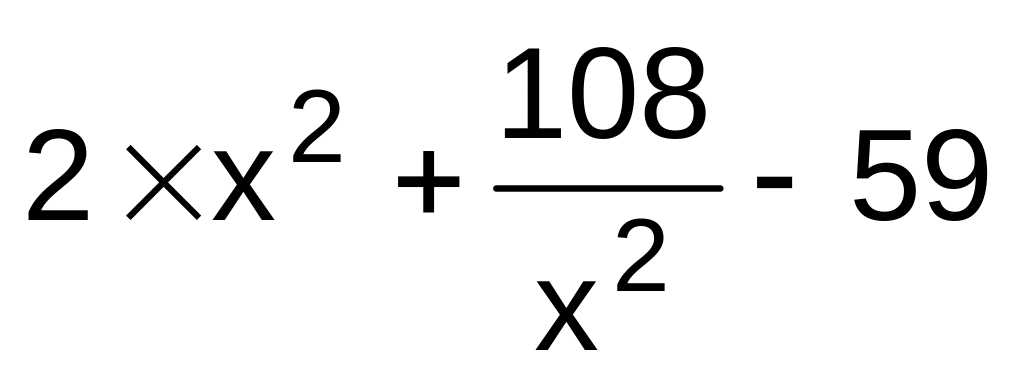 ,
a5.0,
b1.0,
x16.0,
x22.5.
,
a5.0,
b1.0,
x16.0,
x22.5.f(x)
 ,
a9.0,
b1.0,
x110.0,
x22.0.
,
a9.0,
b1.0,
x110.0,
x22.0.f(x)
 ,
a0.8,
b0.8,
x10.2,
x21.0.
,
a0.8,
b0.8,
x10.2,
x21.0.f(x)
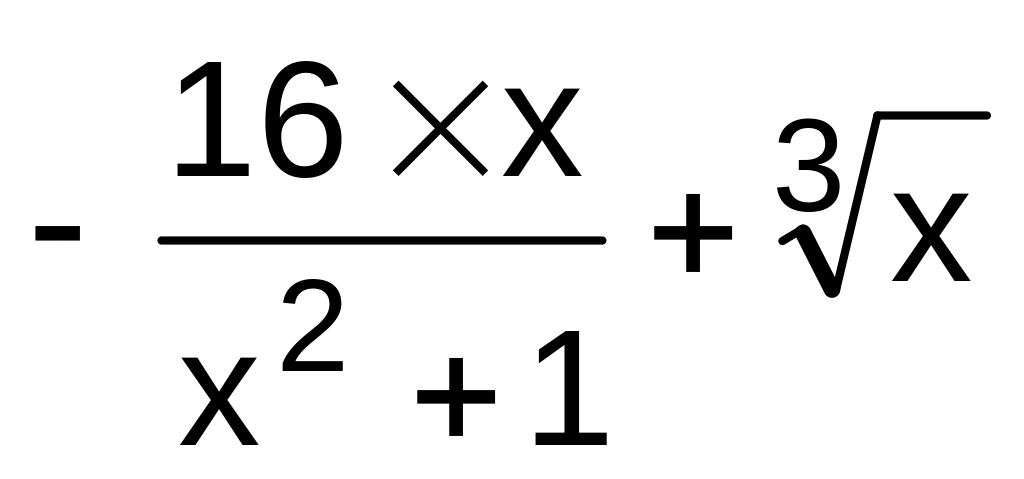 ,
a0.0,
b6.0,
x11.0,
x27.0.
,
a0.0,
b6.0,
x11.0,
x27.0.f(x)8x2
 8
,
a0.4,
b2.0,
x10.6,
x22.4.
8
,
a0.4,
b2.0,
x10.6,
x22.4.f(x)8

 ,
a6.5,
b2.5,
x16.0,
x21.5.
,
a6.5,
b2.5,
x16.0,
x21.5.f(x)
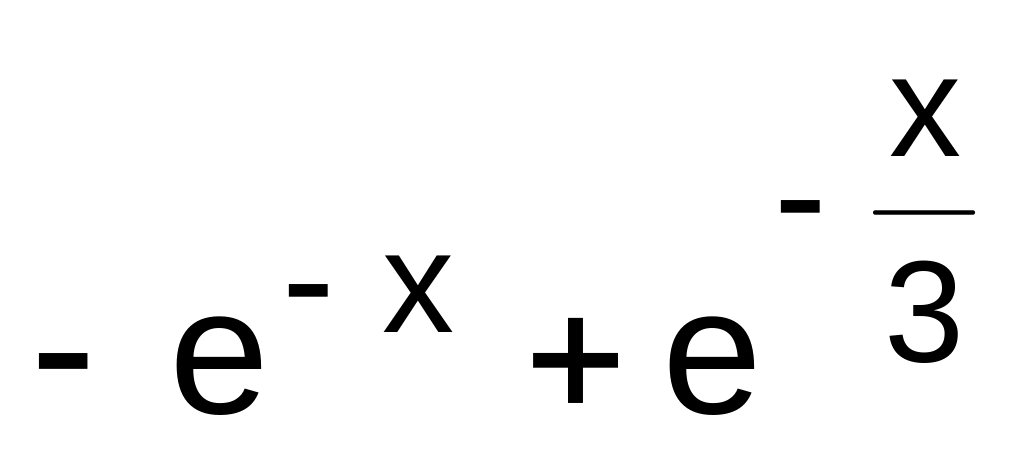 ,
a0.0,
b6.0,
x11.0,
x27.5.
,
a0.0,
b6.0,
x11.0,
x27.5.f(x)
 ,
a3.0,
b9.0,
x12.0,
x27.0.
,
a3.0,
b9.0,
x12.0,
x27.0.f(x)
 ,
a6.0,
b0.0,
x18.0,
x22.0.
,
a6.0,
b0.0,
x18.0,
x22.0.f(x)
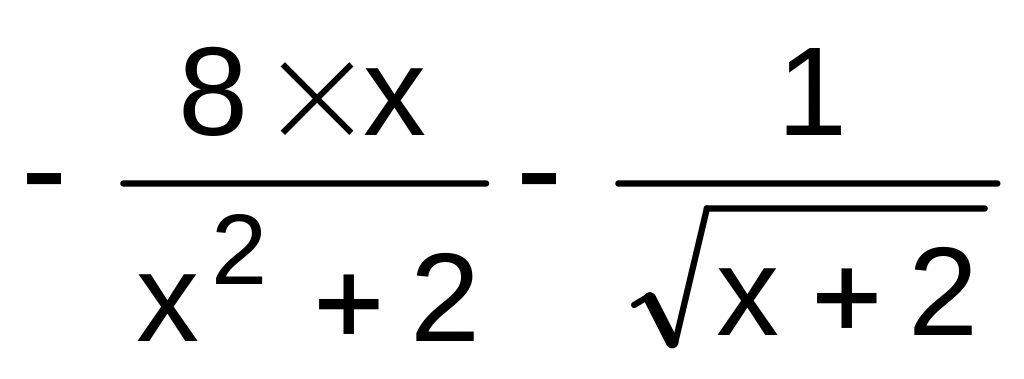 ,
a1.8,
b0.2,
x11.6,
x20.2.
,
a1.8,
b0.2,
x11.6,
x20.2.f(x)
 ,
a1.0,
b0.2,
x11.2,
x20.3.
,
a1.0,
b0.2,
x11.2,
x20.3.f(x)
 ,a2.4,b0.8,
x10.4,
x21.2.
,a2.4,b0.8,
x10.4,
x21.2.f(x)
 ,
a1.0,
b5.0,
x11.5,
x26.0.
,
a1.0,
b5.0,
x11.5,
x26.0.f(x)
 ,
a12.0,
b18.0,
x111.0,
x216.0.
,
a12.0,
b18.0,
x111.0,
x216.0.
Пример. (См. ОБРАЗЕЦ).
Б. Предел функции
Задача.
Вычислить
![]() для f(x) номер
W при трех значениях a.
для f(x) номер
W при трех значениях a.
f(x)
 ,
a{,
3,
3}.
,
a{,
3,
3}.f(x)
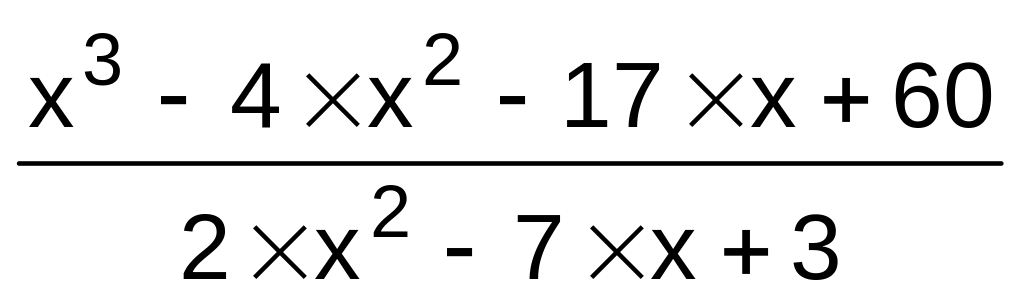 ,
a{,
2,
3}.
,
a{,
2,
3}.f(x)
 ,
a{,
3,
1}.
,
a{,
3,
1}.f(x)
 ,
a{,
2,
2}.
,
a{,
2,
2}.f(x)
 ,
a{,
1,
3}.
,
a{,
1,
3}.f(x)
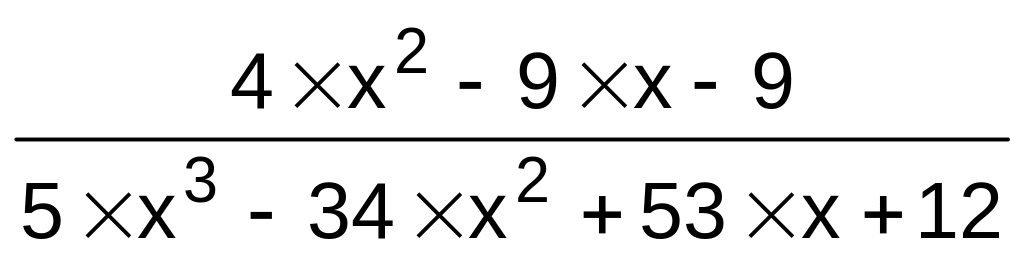 ,
a{1,
,
3}.
,
a{1,
,
3}.f(x)
 ,
a{1,
,
1}.
,
a{1,
,
1}.f(x)
 ,
a{1,
,
2}.
,
a{1,
,
2}.f(x)
 ,
a{1,
,
3}.
,
a{1,
,
3}.f(x)
 ,
a{1,
,
3}.
,
a{1,
,
3}.f(x)
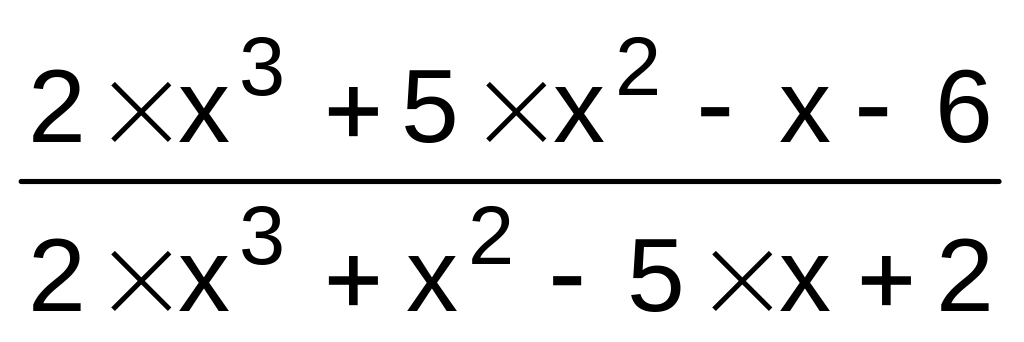 ,
a{,
5,
1}.
,
a{,
5,
1}.f(x)
 ,
a{,
2,
2}.
,
a{,
2,
2}.f(x)
 ,
a{3,
,
3}.
,
a{3,
,
3}.f(x)
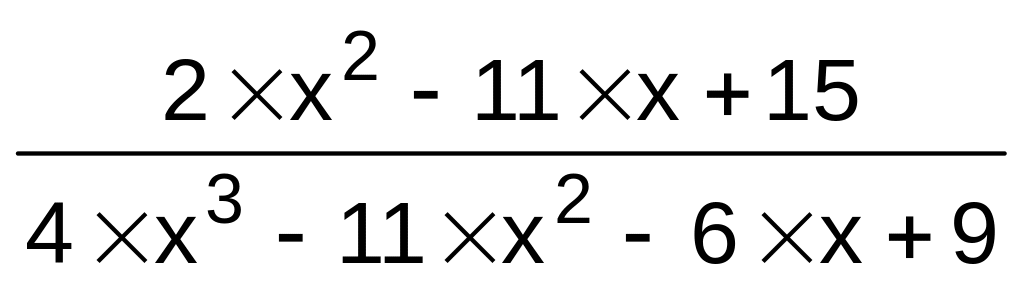 ,
a{2,
,
3}.
,
a{2,
,
3}.f(x)
 ,
a{,
1,
1}.
,
a{,
1,
1}.f(x)
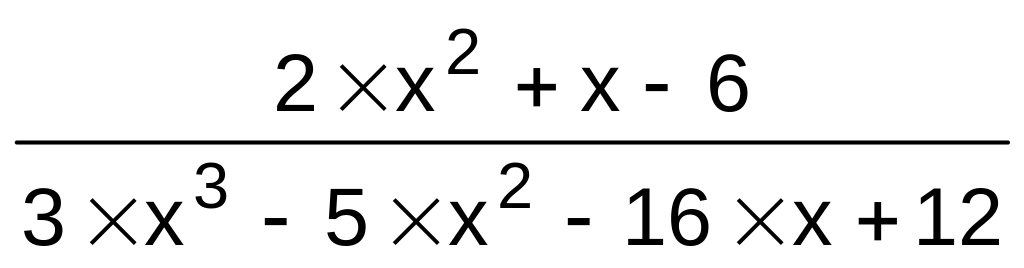 ,
a{,
3,
2}.
,
a{,
3,
2}.f(x)
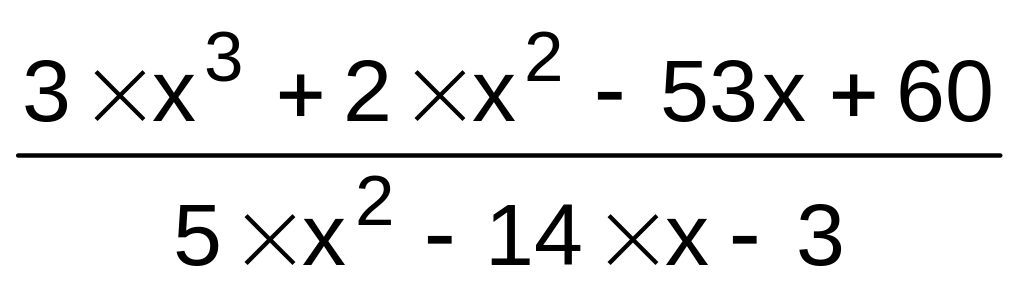 ,
a{,
1,
3}.
,
a{,
1,
3}.f(x)
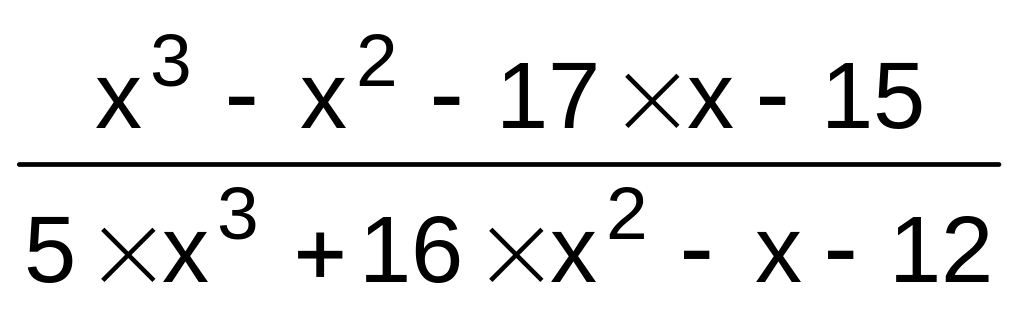 ,
a{3,
,
1}.
,
a{3,
,
1}.f(x)
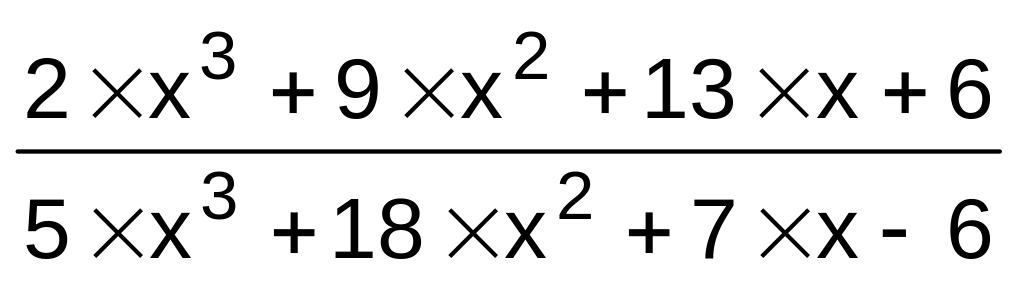 ,
a{1,
,
1}.
,
a{1,
,
1}.f(x)
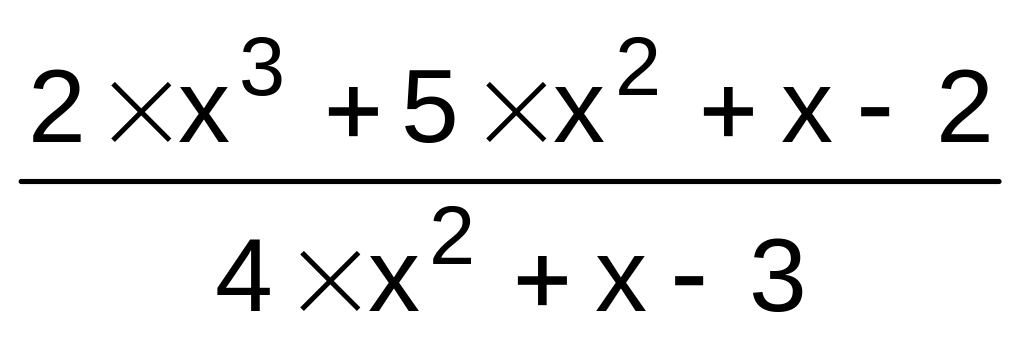 ,
a{,
3,
1}.
,
a{,
3,
1}.
Пример W18.
f(x)![]() ,
a{,2,
2}.
,
a{,2,
2}.
Решение.
a, ![]()
n3, m2, nm, x, nm1, нечетное.
a2, ![]()
![]()
![]()
![]() .
.
a2, ![]()
|
4x325x238x8 |
|
x2 |
|
|
4x211x6 |
|
x2 |
||||
4x3 8x2 |
|
4x217x4 |
|
4x2 8x |
|
4x3 |
||||||
|
|
17x238x |
|
|
|
|
|
3x6 |
|
|
||
|
17x234x |
|
|
|
|
3x6 |
|
|
||||
|
|
|
|
4x 8 |
|
|
|
|
|
0 |
|
|
|
|
|
4x 8 |
|
|
|
|
|
|
|
||
|
|
|
|
0 |
|
|
|
|
|
|
|
|
![]()
!
!
Раскрываем эту неопределенность. Как видим, и числитель, и знаменатель f(x) обращается в нуль при xa2. Поэтому и числитель, и знаменатель f(x) делится на (x2). Процедура деления и ее результаты показаны выше.
Значит,
![]()
![]()
![]() .
.
