Глава 5. Основы дифференциального исчисления

2. в) y’ ,

д) y’(arccos(x))’ 

  .

9. б) e^1.05e^1+0.05e^x+x

e^x+xe^x(e^x)’xe^xe^xxe^x(1x)

e1.052.854.

Глава 6. Основы интегрального исчисления

8. б) F .

Этап 1.

F(x) 

 

 .

Этап 2.

FF_NL   .

10. а) По формуле Ньютона-Лейбница.

F .

Этап 1.

F(x) xt, dtdx, dxdt

  .

Этап 2.

FF_NLe^x e^x e¹e^32.720.052.67.

б) Методом Рунге-Ромберга по формуле трапеций.

0. Cтроим таблицу {xt_i, yt_i} функции f(x) на отрезке [a, b] объемом n4:

h 1, xt₀a1, xt_i1xt_ih, i , yt_if(xt_i), i .

i	0	1	2	3	4
xti	1.0	0.0	1.0	2.0	3.0
yti	2.72	1.00	0.37	0.14	0.05
j	0		1		2

1. По таблице {xt_i, yt_i} вычисляем значение F_h:

F_h 

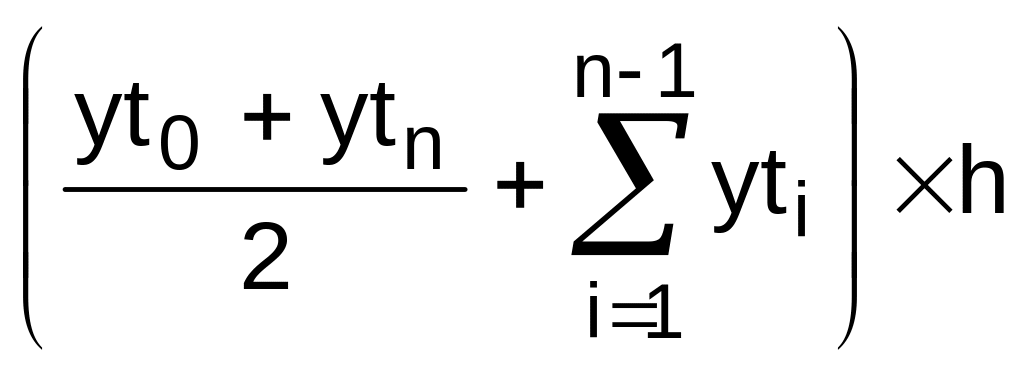
 2.89.

2. Формируем таблицу {xt2_j, yt2_j}. Выделяем в таблице {xt_i, yt_i} столбцы с четными номерами, заново их нумеруем подряд j , находим n2 2, h22h2.

По таблице {xt2_j, yt2_j} вычисляем значение F_2h:

F_2h 

 3.51.

3. Вычисляем поправку Рунге:

PR 0.20.

4. Вычисляем значение интеграла по формуле Рунге-Ромберга:

FF_RRF_hPR2.69.

5. Проверяем контрольное условие:

F_NLF_RR0.02PR0.20.

Раздел III. Основы теории вероятностей

Глава 7. Понятие вероятности

6. Дополним картину еще одним из возможных результатов – ничьей Н. Тогда {A,B,H}. По смыслу задачи события A, B и H – несовместные (результатом игры может быть только одно из этих событий): ABAHBH. Поэтому

а) событие B (второй не выиграл) означает, что выиграл первый или партия закончилась вничью, то есть BAH. Точно так и событие ABH,

б) событие AB (не выиграл первый и не выиграл второй) – однозначно ничья:

AB10’(AB)ABHH12Н.

в) событие AB (не выиграл первый, или не выиграл второй, или не выиграл ни тот, ни другой) означает, что возможен любой исход игры. Действительно,

AB(AB)AB.

12. а) Сухов выберет все три вопроса, на которые знает ответы:

   0.198.

13. Проверяется три дела. Событие «взято дело о краже» обозначим как К, событие «взято дело не о краже» – как Н.

а) Тогда событие А – «среди трех взятых на проверку дел два о краже» суть:

АККНКНКНКК,

вероятность которого вычисляют так:

P(A)   

 0.089.

16. а) Событие второй билет выигрышный В2 наступает при выполнении двух гипотез: первым был тоже выигрышным В1, первым был невыигрышным Н1. По формуле полной вероятности вычисляем

P(В2)P(В1)P(В2В1)P(В2)P(В2Н1)

     .

б) По формуле Байеса апостериорная вероятность гипотезы В1 суть

P(В1В2)    .

18. Вероятность того, что клиент берет вклад p , вероятность того, что вклад он брать не будет q .

а) это событие укладывается в схему Бернулли при n6, m2:

 p²q⁴   

53⁵  0.3.

19. Данный случайный эксперимент укладывается в схему Бернулли с параметрами p0.2 (20% попаданий) и q0.8. Событие «хотя бы один раз»ХО противоположно событию «ни одного раза»НО. По условию задачи P(ХО)0.9, а P(НО)1P(ХО)0.1. Но с другой стороны, по формуле Бернулли P(НО)  . Значит,

0.1 , ln(0.1)nln(0.8), n 10.32.

Для того чтобы с вероятностью 0.9 поразить мишень потребуется 11 выстрелов.