Ответы к задачам

Каждая глава завершается параграфом «Вопросы и задачи для самоконтроля». Читателю предлагается самостоятельно ответить на вопросы и решить задачи. Далее приведены ответы и решения к наиболее сложным задачам.

Раздел I.

ОСНОВАНИЯ МАТЕМАТИКИ

Глава 1. Элементы теории множеств

6. а) A(AB)<3>(AA)(AB)

<5>(AB)<4’>AB.

б) (AB)(AB)<3’>A(BB)

<5>A<4’>A.

в) (AB)(AB). Решаем задачу графически (рис. в). Сформируем отдельно левую (AB) и правую (AB) части утверждения. Как видим, они одинаковы. Значит, утверждение (AB)(AB) верно.

г) Утверждение (AB)(AB) верно, потому что оно дуально только что доказанному утверждению в).

7. 2A\(BC); 6(AB)\C; 8ABC.

9. а) ИБЗИ; б) ИБЗИ;

в) ИБ\ЗИ; г) ЗИ\ИБ.

Глава 2. Числа

4. (1000)_mod1912, (1000)_mod100, (1000)_mod64.

(73)_mod1916, (73)_mod101, (73)_mod61.

(7)_mod197, (7)_mod67, (7)_mod103.

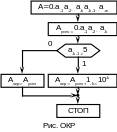6. См. рис. ОКР.

8. Некомплект судей:

а) в Гончарове: 38%;

б) в Тургеневе: 28%.

Значит, в Гончарове дела хуже.

Глава 3. Элементы математической логики

5. д) Обозначим высказывание «если a>b, а b>c, то v=w» как A, a>b – как x₀, b>c – как x₁, vw – как x₂. Тогда

A(x₀x₁)x₂ (табл. 5).

8. R(x₂x₁x₀)(x₂x₁x₀)(x₂x₁x₀)(x₂x₁x₀)

(x₂x₁x₀)(x₂x₁x₀)(x₂x₁x₀)(x₂x₁x₀)9

(x₂x₁)(x₂x₁)(x₂x₁)(x₂x₁)9x₂x₂51.

9. б) ((AA)A)((AA)A)<7>

(AA)AA<12>AA<5>1.

Таблица 5,г
x2	x1	x0	x0x1	Y
0	0	0	0	1
0	0	1	0	1
0	1	0	0	1
0	1	1	1	0
1	0	0	0	1
1	0	1	0	1
1	1	0	1	1
1	1	1	1	1

Остальные утверждения доказываются аналогично.

Раздел II. Основы математического анализа

Глава 4. Функции

	Таблица ПОФ
y2-x	x	1	0	1	2	3	y	ylog2(x)
	y	2	1				x

4. Делаем замену: x2^-y. Отсюда ylog₂(x) – функция, обратная исходной. Строим таблицу прямой функции. Таблицу обратной функции получим, поменяв местами строки таблицы прямой функции (табл. ПОФ).

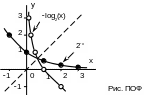
По данным этой таблицы строим графики прямой и обратной функций (рис. ПОФ).

15. а)

.

в)  .

г) n5, m5, nm, a_n1, b_m3 .

д)  

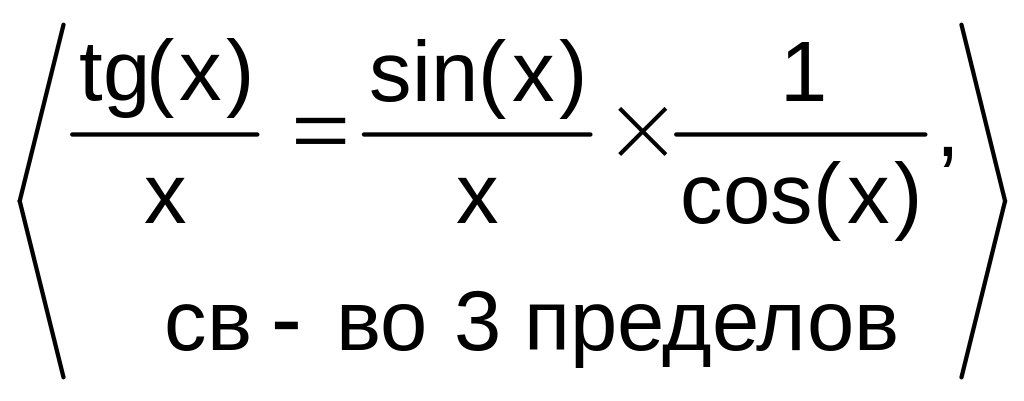
 1 

прямая подстановка1.

е)  

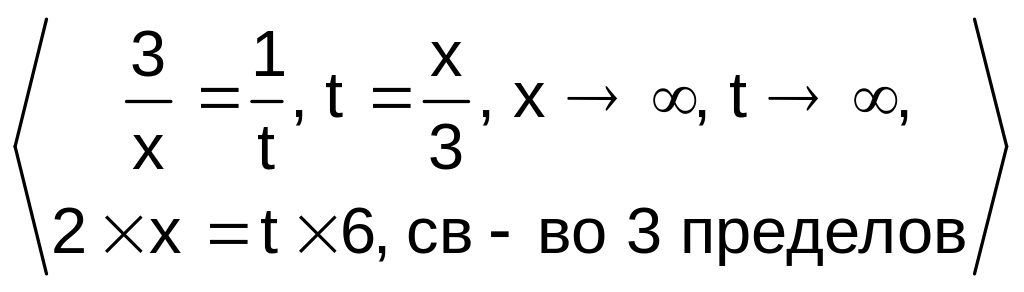
 e⁶403.43.