8.5. Энтропия и информация

Во второй половине XX века человечество вступило в новую стадию своего цивилизационного развития, которая названа информационным обществом. В нашей стране разработана "Стратегия развития информационного общества в Российской Федерации" (утв. Президентом РФ 07.02.2008 N Пр-212). Основные черты информационного общества в стратегии определены так.

Информационное общество характеризуется высоким уровнем развития информационных и телекоммуникационных технологий и их интенсивным использованием гражданами, бизнесом и органами государственной власти.

Увеличение добавленной стоимости в экономике происходит сегодня в значительной мере за счет интеллектуальной деятельности, повышения технологического уровня производства и распространения современных информационных и телекоммуникационных технологий.

Существующие хозяйственные системы интегрируются в экономику знаний. Переход от индустриального к постиндустриальному обществу существенно усиливает роль интеллектуальных факторов производства.

Международный опыт показывает, что высокие технологии, в том числе информационные и телекоммуникационные, уже стали локомотивом социально-экономического развития многих стран мира, а обеспечение гарантированного свободного доступа граждан к информации – одной из важнейших задач государств.

Информационные технологии представляют собой организованное научно-методическое обеспечение переработки информации.

Переработка информации – это совокупность таких информационных процессов:

производство информации: генерация, включая моделирование; рецепция, измерение,

интерпретация информации: преобразование, логическая обработка, аккумуляция,

коммуникация информации: передача, хранение, представление.

Информация, как видим, является предметом и продуктом информационных технологий.

Юридическая деятельность осуществляется в сфере социальных систем и явлений, то есть в сфере отношений между людьми. Поэтому в этой сфере естественно использовать тот смысл термина «информация», который определен ст. 2 Федерального Закона "Об информации, информационных технологиях и о защите информации":

информация – сведения (сообщения, данные) независимо от формы их представления.

В сфере юриспруденции применяются две формы представления информации.

Вербальная (словесная) форма, когда сведения задаются устной или письменной речью. Она используется для качественной характеристики объектов и процессов. Такая форма фиксации и передачи информации принята в большинстве правовых актов.

Числовая форма (форма данных), когда сведения задаются количественными характеристиками объектов и процессов. А эти характеристики получены путем наблюдений, измерений, путем обработки их результатов с использованием математических методов.

Современные информационные технологии реализуются на компьютерах. И вся информация в компьютерах представлена в числовой форме, а именно, двоичными кодами. Следовательно, числовая форма представления информации является универсальной.

Отметим, что каждый из двух первых информационных процессов (производство и интерпретация информации) начинаются и завершаются третьим, а именно, коммуникацией информации. Коммуникация информации – это передача ее в пространстве по каналам связи или во времени посредством хранения на носителях. При передаче информации в пространстве стремятся минимизировать время передачи, а при передаче ее во времени минимизируют пространство (объем носителя).

Главная задача системы коммутации (рис. 8.12) состоит в том, чтобы в достаточной мере обеспечить взаимно-однозначное соответствие между информационными массивами ИМ на ее входе и на ее выходе. Нарушение этого соответствия обусловлено неизбежными помехами той или иной природы, которые воздействуют на систему коммутации. Этим определяется вероятностный характер процессов в системе коммутации. Вероятностный характер имеет и процесс формирования входного ИМ. Случайным событием здесь является получение того или иного элемента входного массива. Точно так, и получение выходного ИМ носит вероятностный характер, а случайное событие – появление того или иного элемента выходного ИМ.

Рассмотрим некоторое конечное множество X случайных событий x₁,x₂,…,x_N. Любые действия, приводящие к наступлению события x_i, i= , называют, как мы уже знаем, опытом или испытанием, а сам ансамбль x₁,x₂,…,x_N называют пространством элементарных событий . Получение информации в опыте связано с тем, что до его осуществления имеется известная неопределенность в его исходе. Известен полный набор возможных исходов испытания , но какой именно исход наступит в результате опыта, сказать нельзя. По окончании испытания наступает одно из N событий. Тем самым неопределенность относительно результатов опыта уменьшается. Это уменьшение неопределенности относительно результатов испытания после его осуществления и понимают как получение информации. Обозначим количественную меру неопределенности до опыта как H_ДО, а количественную меру оставшейся после опыта неопределенности как H_ПО. Тогда количественной мерой информации I(X) в опытах с множеством X будет разность

Таблица 8.4
i	xi	p(xi)
1	x1	p(x1)
2	x2	p(x2)
¼	¼	¼
N	xN	p(xN)

I(X)=H_ДО-H_ПО. (8.18)

Обычно множество X задают рядом распределения (табл. 8.4). Здесь p(x_i) – вероятность наступления события x_i. Эти вероятности отвечают условию

p(x₁)+p(x₂)+¼+p(x_N)=1. (8.19)

Количественной мерой неопределенно-сти в опытах с конечным множеством случайных событий X является величина H(X), которая называется энтропией:

H(X)=-(p(x₁)´log_a(p(x₁))+p(x₂)´log_a(p(x₂))+¼+

+p(x_N)´log_a(p(x_N)))=

= . (8.20)

Формула (8.20) выведена К. Шенноном в 1948 г. Поясним ее смысл. Для этого перепишем ее так:

H(X)= .

Величину H_i можно назвать собственной неопределенностью случайного события x_i. Тогда величина

H(X)= =

представляет собою математическое ожидание для H_i или среднюю неопределенность исходов опыта с множеством X случайных событий.

В опытах с множеством случайных событий X имеем

H_ДОH(X).

Результатом опыта является исход x_i и только он. Такой исход является достоверным, действительно наступившим в опыте. Это значит, что при наступлении достоверного исхода неопределенность отсутствует, то есть

H_ПО0,

и количество информации, полученное в таком испытании

I(X)=H(X).

Опыты описанной категории описывают процессы производства и интерпретации информации.

Перечислим свойства энтропии.

1. Энтропия равна нулю, если в любом опыте с множеством X исход известен заранее: всегда наступает событие x_j и никогда не происходят события x_i, то есть вероятность p_j1, а все вероятности p_i, i¹j равны нулю. Неопределенность в таком опыте отсутствует. А отсутствие неопределенности означает, что энтропия равна нулю.

2. Величина H(X) зависит от вероятностей p(x_i) и достигает максимального значения тогда, когда события x_i равновероятны:

p(x₁)p(x₂)¼p(x_N)=p.

И эти вероятности отвечают условию (8.19): N´p=1. Поэтому

p= .

В этом случае

H(X)= =áN одинаковых слагаемыхñ=

=-N´ =log_a(N).

Формулу

H(X)=log_a(N) (8.21)

для энтропии множества равновероятных событий вывел в 1928 г. американский инженер Р. Хартли. Это была первая попытка количественной оценки энтропии.

Основание a логарифма в формулах (8.20) и (8.21) определяет единицу измерения энтропии. Действительно,

H(X)=log_a(N)=1

тогда, когда a=N. В настоящее время общепринято использование в формулах (8.20) и (8.21) значения a=N=2, что хорошо согласуется с математической логикой и двоичным кодированием информации. Единицей измерения энтропии, а значит, и информации при a=2 является бит (англ. bit от сжатия слов binary digit). История науки знает случаи использования и таких единиц, как нит (a=e) и дит (a=10). Один бит равен 1.44 нит (log₂(e)) или 3.32 дит (log₂(10)).

Пример. Пусть некто первый случайным образом загадывает целое число из диапазона X=[0,15]. При этом он никогда не загадывает круглые числа, а предпочтение отдает простым числам (табл. 8.5). Вычислим энтропию такого множества случайных событий. В этом случае необходимо применить меру Шеннона (8.20) для N=16. Вычисляем сначала log₂(p(x_i)), потом произведения p(x_i)´log₂(p(x_i)). Далее суммируем эти произведения, знак суммы инвертируем и получаем

Таблица 8.5
i	xi	p(xi)
1	0	0.0000
2	1	0.1250
3	2	0.1250
4	3	0.1250
5	4	0.0179
6	5	0.1250
7	6	0.0179
8	7	0.1250
9	8	0.0179
10	9	0.0179
11	10	0.0000
12	11	0.1250
13	12	0.0179
14	13	0.1250
15	14	0.0179
16	15	0.0179

H(X)=3.351 бита.

Изменим условие задачи так. Некто первый не отдает предпочтения ни одному из этих чисел. Вычислим энтропию множества X.

В данном случае, как и ранее, N=16, но все исходы загадывания равновероятны: p= , и для вычисления энтропии воспользуемся мерой Хартли (8.21):

H(X)=log₂(16)=4 бита.

Как видим, энтропия множества неравновероятных событий меньше энтропии множества равновероятных событий.

Пример. Пусть загадано число 13, и некто второй должен определить загаданное число. Покажем, что для этого достаточно задать первому четыре вопроса (табл. 8.6). Как видим, после ответа на каждый вопрос диапазон чисел, среди которых и загаданное, уменьшается вдвое, и после четвертого вопроса остается одно загаданное число.

Вычислим, какое количество информации получено после ответа на первый вопрос. До ответа на первый вопрос имеем

H_ДО=H(X)=4 бита.

Ответ на первый вопрос показал, что задуманное число находится во второй половине диапазона [0,15]. Значит, вероятности для чисел из первой его половины равны нулю, а вероятности для чисел из второй половины удвоились и составляют 0.1250 (сумма вероятностей для этих чисел отвечает условию (8.19)). Энтропию такого множества неравновероятных событий следует вычислять по формуле Шеннона (8.20). Учтем, что в сумме (8.20) первые восемь слагаемых равны нулю, потому что у них p(x_i)=0 (см. табл. 8.6). Поэтому

Таблица 8.6
Вопрос		-	>7?	>11?	>13?	>12?
Ответ		-	Да.	Да.	Нет.	Да.
i	xi	p(xi)	p(xi)	p(xi)	p(xi)	p(xi)
1	0	0.0625	0	0	0	0
2	1	0.0625	0	0	0	0
3	2	0.0625	0	0	0	0
4	3	0.0625	0	0	0	0
5	4	0.0625	0	0	0	0
6	5	0.0625	0	0	0	0
7	6	0.0625	0	0	0	0
8	7	0.0625	0	0	0	0
9	8	0.0625	0.1250	0	0	0
10	9	0.0625	0.1250	0	0	0
11	10	0.0625	0.1250	0	0	0
12	11	0.0625	0.1250	0	0	0
13	12	0.0625	0.1250	0.2500	0.5000	0
14	13	0.0625	0.1250	0.2500	0.5000	1.0000
15	14	0.0625	0.1250	0.2500	0	0
16	15	0.0625	0.1250	0.2500	0	0
H(X)		4	3	2	1	0
I(X)		0	1	2	3	4

H_ПО= =

=áвосемь одинаковых слагаемыхñ=

= =3 бита.

Значит, количество информации, полученное после ответа на первый вопрос, равно

I1(X)=H_ДО-H_ПО=4-3=1 бит.

Перед ответом на второй вопрос имеем H_ДО=3 бита. Ответ на второй вопрос показал, что задуманное число находится в диапазоне [12,15], и вероятности для каждого из чисел этого диапазона равны 0.2500 2^2. Тогда

H_ПО= =2 бита.

I2(X)=H_ДО-H_ПОI1(X)3-21=2 бита.

Перед ответом на третий вопрос имеем H_ДО=2 бита. Ответ на третий вопрос показал, что задуманное число находится в диапазоне [13,14], и вероятности для каждого из чисел этого диапазона равны 0.5000 2^1. Тогда

H_ПО= =1 бит.

I3(X)=H_ДО-H_ПОI2(X)=2-12=3 бита.

Перед ответом на четвертый вопрос имеем H_ДО=1 бита. После ответа на четвертый вопрос остается только искомое число 13 с вероятностью, равной 1, то есть H_ПО=0.

I4(X)=H_ДО-H_ПОI3(X)=1-03=4 бита.

Значит, полная информация, полученная в ответах на четыре вопроса, составит

I(X)=I4(X)=H(X)=4 бита.

Положим, что в опыте одновременно участвуют и множество X с энтропией H(X), и множество Y с энтропией H(Y). Результатом того или иного испытания может быть и исход x_i из X, и исход y_j из Y, то есть событие x_iy_j (i= , j= ). Говорят, что в таком опыте оперируют с множеством X´Y. Если события x_i и y_j независимы, то

p(x_iy_j)p(x_i)p(y_j),

а энтропия H(X´Y) множества X´Y, когда x_i и y_j независимы, равна

H(X´Y)=H(X)+H(Y). (8.22)

Формула (8.22) справедлива для любого числа k участвующих в опыте множеств. А если все они еще и одинаковы, то есть оперируют с множеством X^k, то

H(X^k)=k´H(X).

Пример. Из 32 символов множества X составляют сообщения из трех символов. Какое количество информации несет такое сообщение?

Здесь множество случайных событий X мощностью N=32. Ни один из символов не имеет преимуществ перед другими, то есть все они равновероятны в одной выборке. Значит, энтропия множества X при выборе одного символа вычисляется по формуле Хартли:

H(X)=log₂(N)=log₂(32)=5 битов.

При выборе трех символов множество X используется k=3 раза, то есть в сообщениях из трех символов оперируют с множеством X³, а элементом этого множества является любое трехсимвольное сообщение. Тогда энтропия множества X³ равна

H(X³)=3´H(X)=15 битов.

До составления того или иного сообщения неопределенность в исходе этого опыта есть

H_ДО=H(X³))=15 битов.

После формирования конкретного сообщения неопределенность в исходе опыта отсутствует. А это означает, что

H_ПО=0.

Значит,

I(X)=H_ДО-H_ПО=15 битов.

Отметим, что общее количество k-символьных сообщений, которые можно составить из N символов равно N^k, потому что в каждую из k позиций для сообщения можно поместить любой из N символов. В нашем примере из 32 символов можно составить 32³=2¹⁵=32768 трехсимвольных сообщений.

Положим теперь, что события x_i и y_j зависимы. Тогда

p(x_iy_j)p(x_i)p(y_jx_i)p(y_j)p(x_iy_j),

где

p(y_jx_i) – условная вероятность события y_j, а именно, вероятность события y_j, вычисленная при том условии что x_i произошло,

p(x_iy_j)– условная вероятность события x_i, а именно, вероятность события x_i, вычисленная при том условии что y_j произошло.

Энтропия H(X´Y) множества X´Y, когда x_i и y_j зависимы, равна

H(X´Y)=H(Y)+H(XY)=H(X)+H(YX)). (8.22)

Здесь

H(XY) – условная энтропия множества X. Она характеризует среднюю неопределенность множества X, которая остается после наступления того или иного события из множества Y,

H(YX) – условная энтропия множества Y. Она характеризует среднюю неопределенность множества Y, которая остается после наступления того или иного события из множества X.

С условными энтропиями оперируют в системах коммутации.

На вход системы поступает сообщение x_i из входного ИМ X. На выходе системы коммутации появляется сообщение y_j из выходного ИМ Y. Получив сообщение y_j, нельзя утверждать, что оно точно совпадает с сообщением x_i поскольку система коммутации подвержена воздействию помех. Таким образом, выходной ИМ Y отображает входной ИМ X со средней неопределенностью H(XY). До выполнения опыта со входным ИМ X неопределенность его исхода характеризуется энтропией

H_ДОH(X).

После опыта о его результате судят по выходному ИМ Y с неопределенностью

H_ПОH(XY).

Количество информации I(X,Y) о событиях входного ИМ X, которое получают в событиях выходного ИМ Y, вычисляют так:

I(X,Y)H(X)H(XY). (8.23)

Точно так, имея сообщение x_i, нельзя утверждать, что оно совпадает с сообщением y_j. То есть входной ИМ X отображает выходной ИМ Y со средней неопределенностью H(YX). До выполнения опыта со выходным ИМ Y неопределенность его исхода характеризуется энтропией

H_ДОH(Y).

После опыта о его результате судят по входному ИМ X с неопределенностью

H_ПОH(YX).

Количество информации I(X,Y) о событиях выходного ИМ Y, которое получают в событиях входного ИМ X, вычисляют так:

I(X,Y)H(Y)H(YX). (8.24)

Рис. 8.13, который называют диаграммой Венна, наглядно иллюстрирует соотношения между описанными энтропийно-информационными понятиями системы коммутации .

Пример. Рассмотрим простейшую систему коммуникации, в которой входной информационный массив X задан всего двумя символами x₁0, x₂1, а выходной – тоже всего двумя символами y₁0, y₂1. Положим, что вероятность ошибки при приеме символа равна p, а вероятность безошибочного приема символа равна 1p.

На рис. 8.14 схематически показана такая система коммуникации. Стрелки показывают, в какие символы множества Y и с какой вероятностью переходит каждый из символов множества X. В теории информации такая система коммуникации называется двоичным симметричным каналом связи.

Вычислять количество информации I(X,Y) будем по формуле (В.7), в которой энтропия H(Y) имеет максимально возможное значение H(Y)1, а условная энтропия H(YX) определяется соотношением (дается без вывода)

H(YX)(plog₂(p)(1p)log₂(1p)). (8.25)

Тогда

I(X,Y)1H(YX) (8.26)

1(plog₂(p)(1p)log₂(1p)).

На рис. 8.15 показаны графики H(YX) и I(X,Y), построенные по формулам (8.25) и (8.26). Как видим, с увеличением p от 0 до 0.5 условная энтропия H(YX) возрастает, а количество информации о массиве X в массиве Y падает.

При p0.5 оказывается, что H(YX)1, а I(X,Y)0. Объясняется это тем, что при p0.5 теряется зависимость между символами массивов X и Y. Когда передается символ x₁0, на выходе с равной вероятностью принимается или символ y₁0, или символ y₂1. То же самое имеет место и при передаче символа x₂1. Значит, при p0.5 неопределенность выходного массива Y при известном входном массиве X максимальна, и элементы массива Y не содержат никакой информации о символах массива X.

С увеличением p от 0.5 до 1 условная энтропия H(YX) падает, а количество информации I(X,Y) растет. Дело в том, что при высокой вероятности ошибки p передача символа x₁0 чаще всего вызывает появление на выходе символа y₂1, а при передаче x₂1 на выходе чаще всего будет y₁0. Если при p0.5 выполнять инверсию символов на выходе (замену нуля на единицу, а единицы на нуль), то вероятность искажения результата инверсии будет равна 1p0.5.

Вопросы и задачи для самоконтроля

1. Сформулируйте понятие случайной величины дискретной и непрерывной.

2. Определить понятие «закон распределения СВ».

3. Определить понятие «ряд распределения» дискретной случайной величины.

4. Определить понятие «функция распределения». Перечислить ее свойства.

5. Определить понятие «плотность распределения». Перечислить ее свойства.

6. Дать определение каждой из числовых характеристик случайной величины дискретной и непрерывной. Что в поведении случайной величины характеризуют ее математическое ожидание и дисперсия?

7. Бросают два игральных кубика. Найти закон распределения и числовые характеристики для суммы выпавших очков.

8. Среди денежных банкнот 20% фальшивых. Наугад берут 3 купюры. Построить ряд распределения и найти числовые характеристики для случайной величины – возможного количества фальшивых купюр в этой выборке.

9. Таблица 8.7
   X	2	5	8	19
   p	0.2	0.3	0.4	0.1

   СВ X задана рядом распределения (табл. 8.7).

Найти математическое ожидание, дисперсию и СКО этой случайной величины.

10. Плотность распределения случайной величины X задана формулой:

f(x)

а) Записать для СВ X функцию распределения F(x).

б) Найти ее числовые характеристики m_x, D_x и _x.

в) Построить графики f(x) и F(x), отобразить на них значения m_x и _x.

г) Вычислить вероятность попадания значений X в интервал ]m_x_x, m_x_x[.

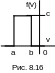11. Плотность распределения случайной величины V задана рис. 8.16. Величины a и b известны.

а) Вычислить значение величины c.

б) Записать аналитические выражения для f(v) и F(v).

в) Найти числовые характеристики для СВ V: m_v, D_v, _v.

г) Вычислить вероятность попадания значений X в интервал ]m_v_v, m_v_v[.

12. Выполнить ДКЗ: Тест 8. СЛУЧАЙНЫЕ ВЕЛИЧИНЫ.

13. Раскрыть содержание понятий информационные технологии и структуру основных информационных процессов.

14. Изложить толкование термина информация в юриспруденции.

15. Охарактеризовать формы представления информации в юриспруденции.

16. Пояснить причину вероятностного характера процессов в системах коммуникации, смысл терминов энтропия и количество информации.

17. Раскрыть содержание меры энтропии по Шеннону и связь этой меры с мерой энтропии по Хартли. Единицы измерения энтропии.

18. В одной урне содержится 10 белых, 20 красных, 30 синих и 40 зеленых шаров, а во второй по 25 шаров каждого из названных цветов. Из каждой урны наугад вынимают по одному шару. Какое количество информации несет сообщение о цвете вынутого шара из каждой урны?

19. Какое минимальное количество двоичных символов потребуется для того, чтобы закодировать символы шестнадцатеричной системы счисления?

20. Энтропия в опытах с несколькими массивами независимых СВ.

21. Сколько четырехсимвольных комбинаций можно составить из символов шестнадцатеричной системы счисления?

22. С помощью диаграммы Венна пояснить смысл понятий:

• условные энтропии H(XY) и H(YX) в опытах с двумя массивами зависимых случайных величин.

• количество информации I(XY) о событиях входного ИМ, которое получают в событиях выходного ИМ.

• количество информации I(YX)о событиях выходного ИМ, которое получают в событиях входного ИМ.

Неправомерный доступ к охраняемой законом компьютерной информации, если это деяние повлекло уничтожение, блокирование, модификацию либо копирование информации, –

наказывается штрафом в размере до двухсот тысяч рублей или в размере заработной платы или иного дохода осужденного за период до восемнадцати месяцев, либо исправительными работами на срок до одного года, либо ограничением свободы на срок до двух лет, либо принудительными работами на срок до двух лет, либо лишением свободы на тот же срок.

(УК РФ, Ст.272, ч. 1)