Глава 8. Случайные величины

8.1. Понятие случайной величины

Нередко результатом случайного эксперимента является числовая величина, значение которой в каждом эксперименте разное. Такая величина называется случайной. Например,

• число попаданий в мишень при трех выстрелах может принимать одно из следующих значений: 0, 1, 2, 3;

• показания ртутного медицинского термометра при измерении температуры пациента принимают одно из следующих значений: 34.1, 34.2,…,36.7,…,42.0.

В первом примере минимальное расстояние между соседними значениями (отсчетами) случайной величины равно единице, во втором – 0.1. Бывают случайные величины и с большими, и меньшими расстояниями между отсчетами.

Случайные величины СВ, у которых расстояние между соседними отсчетами – величина конечная, называются дискретными. Обычно набор значений у дискретных величин конечен (как в приведенных примерах).

В общем случае, дискретные случайные величины – числа рациональные. На числовой прямой они представлены точками, которые разделены конечными промежутками, а длина каждого из промежутков равна единице младшего разряда в записи этих чисел.

В случайных экспериментах действуют и со случайными величинами другой природы. Например,

• вес наугад взятого осколка бомбы,

• ошибка в измерении скорости движения автомобиля.

Возможные значения каждой из таких величин одно от другого не отделены, и образуют на числовой прямой сплошной массив точек. А это вещественные числа.

Случайные величины, у которых значения – суть вещественные числа, называются непрерывными. В общем случае, возможный набор значений непрерывной случайной величины – вся числовая прямая. Работают и с такими непрерывными случайными величинами, значения которых – интервал на числовой прямой.

Если классическая теория вероятностей имеет дело по преимуществу с событиями нечисловой природы, то современная теория вероятностей оперирует с числами – случайными величинами. Это стремятся делать даже и тогда, когда результатом случайного эксперимента число не является.

Например, проводится опыт, в результате которого может наступить или не наступить событие A. Событию A можно сопоставить число X, которое принимает значение 1 при наступлении A, и оно равно 0, когда A не наступило. Теперь X – дискретная случайная величина, которая характеризует событие A. Возможные ее значения – {0,1}.

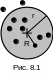
Еще пример. Событие B – попадание при стрельбе в круглую мишень (рис. 8.1). Обозначим радиус круга как r, а расстояние от центра мишени до точки попадания пули как R. Тогда наступлению события B отвечает выполнение неравенства Rr, то есть вероятность события B – не что иное, как вероятность того, что это неравенство выполняются.

Итак, в современной теории вероятностей, где только возможно, от схемы случайных событий переходят к схеме случайных величин. Эта схема предоставляет для решения задач, относящихся к случайным явлениям, более гибкий и универсальный аппарат высшей математики.

8.2. Законы распределения случайных величин

Всякое соотношение, которое устанавливает связь между возможными значениями случайной величины и вероятностями этих значений, называют законом распределения этой СВ.

Изучение законов распределения начнем с дискретных случайных величин.

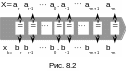
Ряд распределения. Обозначим дискретную СВ как X, а набор ее отсчетов – как x₀, x₁,…, x_n. Исход случайного эксперимента – событие Xx_k характеризуется вероятностью P(Xx_k)p_k. Факт равенства чисел Xx_k устанавливают путем последовательного сравнения цифр в одноименных разрядах записей X и x_k (см. рис. 8.2). Если имеет место a_ib_i для всех ir,r1,,m, то числа X и x_k равны.

Сопоставим каждому отсчету x_k случайной величины X вероятность p_k. В результате получим закон распределения дискретной СВ X. Самой простой формой записи закона распределения дискретной случайной величины является таблица, в первой строке которой перечисляются ее отсчеты x_k, а во второй – вероятности p_k. Такую таблицу {x_k,p_k} и называют рядом распределения.

Очевидно, что события Xx_k, k образуют полную группу, и поэтому .

Пример. Стрелок производит три выстрела по мишени. Вероятность попадания в мишень при каждом выстреле равна 0.6. Построить ряд распределения для числа попаданий в мишень при трех выстрелах.

Обозначим как Z дискретную случайную величину – число попаданий в мишень. Набор ее значений: z₀0, z₁1, z₂2, z₃3. Опыт укладывается в схему Бернулли. Поэтому вероятность события Zz_k вычисляем по формуле Бернулли:

p₀ 0.4³0.064,

p₁  0.60,4²0.288,

p₂  0.6²0.40.432,

p₃ 0.6³0.216.

Теперь составляем табл.8.1 – ряд распределения случайной величины Z.

Таблица 8.1
zk	0	1	2	3
pk	0.064	0.288	0.432	0.216

Закон распределения для непрерывных СВ задается функцией распределения и/или плотностью распределения.

Функция распределения. Напомним, что непрерывная СВ X – число вещественное. Точно так и возможное ее значение величина x – точка в сплошном массиве точек на числовой оси тоже число вещественное. В записи каждого вещественного числа дробная часть имеет бесконечную длину. Поэтому для вещественных чисел нельзя установить факт их равенства в силу того, что процедуру последовательного сравнения цифр в одноименных разрядах записей завершить невозможно. Зато путем последовательного сравнения цифр в одноименных разрядах этих записей можно установить факт a_jb_j, jr, r1,…(см. рис. 8.3), а, значит, и факт Xx. На этом процедура последовательного сравнения цифр в одноименных разрядах записей X и x завершается.

При построении закона распределения непрерывной случайной величины X оперируют с событием Xx. Это неравенство можно зафиксировать путем последовательного сравнения цифр в одноименных разрядах записей X и x. Напомним, что здесь X – результат случайного эксперимента, а x – любая точка на числовой прямой, то есть x является независимой переменной. Значит, вероятность события Xx есть некоторая функция переменной x. Ее и называют функцией распределения случайной величины X и обозначают как F(x):

F(x)P(Xx). (8.1)

Прежде чем двигаться дальше, отметим глубокий философский смысл этого определения. В левой части (8.1) записана функция действительного аргумента, а в правой – вероятность некоторого события. Функция является одним из фундаментальных понятий математического анализа, той области математики, где изучаются жестко определенные закономерности. Вероятность – фундаментальное понятие теории вероятностей, которая изучает закономерности в мире случайного. Формула (8.1) перебрасывает мост между математическим анализом и теорией вероятностей. Тем самым строгий, хорошо разработанный аппарат математического анализа становится мощным инструментом исследования случайных величин в теории вероятностей.

Перечислим общие свойства функции распределения.

1. Функция F(x) – неубывающая функция своего аргумента, то есть при x₂x₁ и F(x₂)F(x₁).

2. F()1.

3. F()0.

К этим свойствам приведем геометрические пояснения (рис. 8.4). Пусть x – точка на оси 0x. Случайная величина X в результате опыта может занять на этой же оси то или иное положение. Тогда F(x)P(Xx) – вероятность того, что X попадет в зону на оси левее точки x (в заштрихованную зону). При увеличении x заштрихованная область левее него увеличивается. Поэтому вероятность P(Xx) уменьшиться не может. Следовательно, F(x) с ростом x не убывает (свойство 1).

Очевидно, что при x заштрихованная область левее x становится бесконечно большой, и попадание в нее X оказывается событием достоверным. Поэтому F()P(X)1 (свойство 2). Точно так, при x попадание X левее x становится невозможным, и F()P(X)0 (свойство 3).

Пример. Функция распределения непрерывной случайной величины W задана формулой:

F(w) (8.2)

График этой функции показан на рис. 8.5,а. Как видим, F(x) обладает всеми указанными свойствами.

Плотность распределения. Для непрерывной случайной величины X функция распределения F(x) непрерывна, а значит, и дифференцируема на всей числовой оси. Продифференцировав F(x), получим функцию

f(x)F’(x), (8.3)

которая называется плотностью распределения или плотностью вероятности (по аналогии с плотностью вещества).

Пример. Плотность распределения f(w) случайной величины, у которой F(w) задана формулой (8.2):

f(w) (8.4)

На рис. 8.5,б показан график плотности распределения (8.4). Его называют кривой распределения непрерывной СВ.

Рассмотрим свойства плотности распределения.

1. Плотность распределения – функция неотрицательная:

f(x)0 для x.

2. Полная площадь под кривой распределения равна единице:

(событие X достоверно, его вероятность равна единице).

Отметим важное обстоятельство. Случайная величина X обычно имеет размерность. Отсчеты функции F(x) размерности не имеют. А вот отсчеты f(x) имеют размерность, обратную размерности случайной величины X.

Когда задана функция распределения F(x) плотность вероятности f(x) вычисляют по формуле (8.3). А если задана плотность распределения f(x), то функцию распределения F(x) вычисляют так:

F(x) . (8.5)

Поэтому функцию F(x) называют интегральным законом распределения, а функцию f(x) называют дифференциальным законом распределения непрерывной СВ.

Вероятность попадания случайной величины в заданный диапазон. Зададим на оси 0x две точки a, b и вычислим вероятность такого события aXb, а именно, вероятность того, что случайная величина X в результате опыта попадет в диапазон, ограниченный точками a и b. Для этого рассмотрим такие события (рис. 8.6):

A: Xb, B: Xa, C: aXb.

События B и C несовместны, так как X не может оказаться одновременно и слева, и справа от точки a. Событие A – сумма событий B и C: ABC (рис. 8.6). По формуле сложения вероятностей для несовместных случайных событий имеем:

P(Xb)P(Xa)P(aXb)

или с учетом определения (8.1)

F(b)F(a)P(aXb).

Откуда следует, что

P(aXb)F(b)F(a).

Таким образом, вероятность попадания случайной величины в заданный диапазон равна приращению ее функции распределения на этом диапазоне.

Укажем на любопытное следствие из последней формулы. Пусть X – непрерывная случайная величина. Будем неограниченно уменьшать размер диапазона путем ba. В результате получим событие Xa, вероятность которого есть

P(xa)  0.

Как видим, вероятность отдельного точечного значения непрерывной случайной величины равна нулю! Другими словами, для непрерывной случайной величины вероятность события Xa равна нулю, но событие это возможно (результат случайного эксперимента X может попасть в точку a на числовой прямой). Поскольку P(Xa)0, неравенства aXb эквивалентны неравенствам aXb. Эти строгие неравенства и используют при вычислении вероятности попадания случайной величины в заданный диапазон (в интервал ]a,b[)

P(aXb)F(b)F(a). (8.6)

Пример. Вычислить вероятность попадания СВ W, для которой функция распределения F(x) определена формулой (8.2), в диапазон от a1 до b3.

Когда задана F(x) (см. рис. 8.5,а), действуем по формуле (8.6),:

P(1W3)F(3)F(1)0.950.630.32.

Приращение функции распределения на интервале ]1,3[, а именно, число F(3)F(1)P(1W3)0.32 показано на рис. 8.5,а.

Если же задана плотность распределения f(x), вероятность события aXb вычисляется так:

P(aXb) . (8.7)

Таким образом, вероятность попадания случайной величины в заданный диапазон равна площади под кривой f(x) на интервале ]a,b[.

Пример. Плотность вероятности f(x) случайной величины W задана формулой (8.4). Вычислить вероятность попадания W в диапазон от a1 b3. Действуем по формуле (8.7):

P(1X3) F(3)F(1)0.32.

Теперь число P(1X3)0.32 – заштрихованная площадь под кривой f(x) на интервале ]1,3[ (см. рис. 8.5,б).