7.2. Случайные события

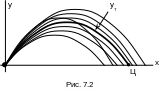
Окружающий нас мир полон таких явлений, которые имеют случайный характер. Например, производится стрельба из орудия, установленного под углом к горизонту (рис. 7.2). Теоретически траектория снаряда представляет собою параболу

y_Т(x)ax²bxc, (7.8)

и все выпущенные снаряды должны попадать в одну и ту же точку Ц. Однако практика показывает, что при каждом новом выстреле фактическая траектория очередного снаряда неизбежно отличается от y_Т(x). Обусловлено это влиянием многих факторов (порывами ветра, различиями в весах зарядов и др.). Эти факторы при выводе формулы (7.8) не учитываются, да и вряд ли могут быть учтены.

Итак, случайное явление при многократном воспроизведении протекает всякий раз по-новому. Элементы неопределенности, сложности, многопричинности, присущие случайным явлениям, требуют специальных методов для изучения этих явлений. Такие методы и разрабатываются в теории вероятностей. Предметом теории вероятностей являются специфические закономерности, которые наблюдаются в случайных явлениях.

Практика показывает, что в большой массе однородных случайных явлений обнаруживаются вполне определенные закономерности, свойственные именно массовым случайным явлениям. Например, при ограниченном числе выстрелов (рис. 7.2) точки разрыва снарядов относительно точки Ц расположены в полном беспорядке, без какой-либо видимой закономерности. По мере увеличения числа выстрелов в расположении точек разрыва наблюдается устойчивая закономерность: густота разрывов по мере удаления от точки Ц убывает по вполне определенному закону, который называется нормальным.

Следует особо подчеркнуть, что методы теории вероятностей по природе своей приспособлены только для исследования массовых случайных явлений. Они не дают возможности предсказать, к чему приведет отдельное случайное явление, но дают возможность предсказать средний суммарный результат массы однородных случайных явлений. Например, интуиция подсказывает, а практика подтверждает, что при большом числе бросаний монеты герб выпадает в половине бросков (первые две строки в табл. 7.1). Если же сделать несколько бросков, этой закономерности не видно (две последние строки в табл. 7.1).

Таблица 7.1
Экспериментатор	Число бросаний	Число гербов
Бюффон	4040	2048
Пирсон	24000	12012
Королев	4	3
Радионов	5	1

Во всех случаях, когда применяются вероятностные методы, их цель в том, чтобы, минуя слишком сложное (а зачастую и невозможное) описание отдельного явления, обратиться прямо к законам, которые управляют массами случайных явлений. Эти законы позволяют не только осуществить научный прогноз в заданной области случайных явлений, но в ряде случаев целенаправленно влиять на их ход, ограничивать сферу действия случайности.

Подобно другим отраслям математики, теория вероятностей родилась и развивалась из потребностей практики. Уже в XVII веке были предприняты первые попытки создания общей теории страхования, основанной на анализе закономерностей таких массовых случайных явлений как заболеваемость, смертность людей, несчастные случаи с ними и др. Но как отрасль математики теория вероятностей сформировалась отнюдь не на материалах такого рода практических задач. Эти задачи чрезвычайно сложны, закономерности, управляющие случайными явлениями в них, проявляются недостаточно отчетливо, затушеваны многими осложняющими факторами. Необходимо было сначала выявить и изучить закономерности случайных явлений на более простом материале. Исторически таким материалом оказались азартные игры. Само слово «азарт» (франц. «le hasard») означает «случай». Схемы азартных игр дают исключительные по простоте и прозрачности модели случайных явлений. Поэтому и поныне примеры из области азартных игр широко используются при изучении теории вероятностей как упрощенные модели случайных явлений. Такие примеры в наиболее простом и наглядном виде иллюстрируют основные законы и правила теории вероятностей (скажем, табл. 7.1).

Как и всякая математическая наука, теория вероятностей базируется на системе основных понятий. В качестве первого из них назовем понятие случайного эксперимента.

Случайный эксперимент (опыт, испытание, наблюдение) – это реализация той или иной модели случайного явления.

Например, бросание монеты, игрального кубика, операция с колодой карт, стрельба по мишени, оценка состояния преступности в том или ином регионе за определенный срок и др.

Следующее понятие – случайное событие.

Любой из возможных результатов случайного эксперимента называют случайным событием.

Примеры случайных событий:

А – выпадение герба при однократном броске монеты,

В – появление трех решеток при трех последовательных бросках монеты,

С – появление туза при вынимании карты из колоды,

D – поражение мишени при выстреле,

Е – фиксация более 100 преступлений в регионе за сутки.

Различают события составные и элементарные. Например, такое событие как «Сумма очков, выпавших при бросании двух игральных кубиков, равна шести» имеет место, когда результатом бросания будет любая пара чисел:

{(1,5), (2,4), (3,3), (4,2), (5,1)}.

Это перечисление разбивает составное (сложное) событие «Сумма очков равна шести» на пять элементарных событий. Точно так совокупность

{(1,1), (1,3),..., (3,3),..., (5,5)}

суть разложение на элементарные такого сложного события как «Выпали два нечетных числа». Отметим, что элементарное событие {3,3} входит в разложение и первого, и второго из составных событий.

Элементарное событие – это каждый неразложимый исход случайного эксперимента.

Поэтому дальше полагаем, что термины «элементарное событие» и «исход» – синонимы.

Множество всех взаимно исключающих исходов случайного эксперимента называют пространством элементарных событий

и обозначают символом . Сами элементарные события называют точками пространства . Исходы называют взаимно исключающими, когда при наступлении одного из них остальные не происходят.

Из сказанного следует, что некоторое событие A представляет собою то или иное подмножество пространства . Говорят, что событие A наступило, если опыт заканчивается любым из исходов, входящих в состав подмножества A.

Составное событие, которое включает в себя все исходы пространства , называют достоверным событием, поскольку любой опыт обязательно завершается элементарным событием из множества . Обозначают достоверное событие тем же символом .

Для полноты картины в теории вероятностей вводят в рассмотрение и такой результат испытания, в составе которого нет ни одного исхода. Его называют невозможным событием и обозначают как .

Приведем несколько примеров случайных экспериментов, пространств элементарных событий, их подмножеств.

1. Монету бросают два раза подряд (монета – тонкий, однородный круг). Для этого опыта пространство элементарных событий:

{(Р,Р), (Р,Г), (Г,Р), (Г,Г)},

где Р – выпадение решетки, Г – выпадение герба.

Событие «Выпал хотя бы один герб» – это подмножество {(Р,Г), (Г,Р), (Г,Г)}. Событие «Выпало не более одного герба» – подмножество {(Р,Р), (Р,Г), (Г,Р)}.

2. Бросание игрального кубика (идеального однородного куба). Для этого опыта пространство элементарных событий:

{1,2,3,4,5,6},

здесь число в скобках – количество выпавших очков.

Событие «Выпало четное число очков» – {2,4,6}. Событие «Выпало менее трех очков» – {1,2}.

Основные операции над событиями. Как видим, события – множества. Поэтому существует и алгебра событий.

Суммой событий A и B называют событие C, которое состоит из всех исходов, входящих или в A, или в B, или в оба эти события сразу.

Обозначают сумму событий так:

CAB.

Другими словами, наступление события AB означает, что произошло хотя бы одно из событий A или B (наступило или A, или B, или оба одновременно).

Произведением событий A и B называют событие C, которое включает в себя все исходы, входящие как в A, так и в B.

Обозначают произведение событий так:

CAB.

Иначе, наступление события AB означает, что события A и B произошли одновременно.

Событием, противоположным для A, называют такое подмножество , в которое не входит ни один исход, принадлежащий событию A.

Обозначают событие, противоположное для A, как A. Наступление события A означает, что событие A не произошло.

События A и B называются несовместными, если нет исходов, входящих как в A, так и в B, то есть AB.

Другими словами, несовместность событий A и B означает, что они не могут наступить в одном опыте (совместно), что наступление одного из них исключает наступление другого в одном опыте.

События образуют полный набор, если они несовместны, а их сумма есть достоверное событие .

Например, в урне находятся красные, желтые и синие шары. События «вынут красный шар», «вынут желтый шар», «вынут синий шар» образуют полный набор. Точно так, при бросании игрального кубика события «выпало четное число» и «выпало нечетное число» составляют полный набор. Наряду с термином «полный набор событий» используют термин «полная группа событий».

Приведем примеры из алгебры событий. Бросают игральный кубик. Напомним, что для этого опыта {1,2,3,4,5,6}. Событие A – выпало четное число, A{2,4,6}, B – выпало число, кратное трем, B{3,6}. Тогда

AB{2,4,6}{3,6}{2,3,4,6},

AB{2,4,6}{3,6}{6}, B{1,2,4,5}.

В алгебре событий имеется своя система тождеств, которые сведены в табл. 7.2. Здесь A, B, C – любые события в данном случайном эксперименте.

Каждое тождество можно (и нужно) выразить словами. Например, тождество 5 читается так: в результате данного опыта любое событие либо происходит, либо нет. Тождество 5’: событие не может одновременно и произойти, и не произойти.

Таблица 7.2
1	ABBA		2	ABC(AB)C
1’	ABBA		2’	ABCA(BC)
3	A(BC)(AB)(AC)		4	AA
3’	A(BC)(AB)(AC)		4’	AA
5	AA		6	AA
5’	AA		6’	AA
7	AAA		8	A(AB)A
7’	AAA		8’	A(AB)A
9	(AB)(AB)A		10	(AB)AB
9’	(AB)(AB)A		10’	(AB)AB
11			12	AA
11’	

Как видим, приведенная система тождеств отвечает принципу двойственности. Тождество номер J’ получают из тождества номер J путем замены знака  на знак  (или наоборот), символа  на символ  (или наоборот). Если утверждение номер J (J ) верно, то верно и утверждение номер J’ (и наоборот).

Одни из этих тождеств вытекают прямо из определений для операций алгебры событий, другие нужно доказывать. Скажем, утверждение 5 верно, потому, что слагаемое A – некоторое подмножество , а слагаемое A – такое подмножество , в которое не входят элементы A, и сумма этих подмножеств есть множество . Докажем, к примеру, утверждение 10. Начнем с его левой части. Событие AB означает, что наступило или A, или B, или они произошли одновременно. Событие (AB) противоположно описанному, то есть его наступление означает, что не произошло ни A, ни B. Тот факт, что события A и B не случились одновременно, эквивалентен факту, что одновременно произошли противоположные события A и B, а именно, AB. Но это – правая часть утверждения 10. Значит, и в целом оно верно.